6. Денормирование по частоте

Осуществим переход от нормированной схемы ФНЧ к схеме заданного фильтра согласно [1]. Причем выберем наиболее экономичную (с меньшим числом индуктивностей ) (рис.5)

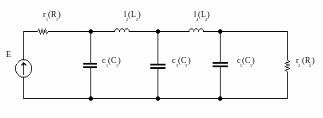
Рис.5 Схема заданного фильтра

Для перехода к денормированным нагрузочному сопротивлению R₂ и граничной частоте f₂ ( т. к. ФНЧ) осуществляется изменение уровня сопротивления и масштаба частоты с помощью следующих множителей:

а ) преобразующий множитель сопротивления:

где R₂ - нагрузочное сопротивление,

r₂ - нормированное нагрузочное сопротивление;

б ) преобразующий множитель частоты:

К оэффицикнты денормирования индуктивности k₁ и емкости k₂ определяются по формулам:

Рассчитаем эти коэффициенты:

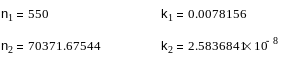
Денормированные значения заданного фильтра определяются по следующим формулам:

7. Расчет частотных характеристик фильтра

После выполнения синтеза электрического фильтра важно убедиться в его соответствии техническим требованиям. Для этого производится расчет частотных характеристик рабочего ослабления А(f) и рабочей фазы B(f) спроектированного фильтра, по которым проверяется выполнение технических требований:

1. рабочее ослабление в ПП не должно превышать заданной величины ΔА:

2. рабочее ослабление в ПН не должно быть ниже заданного значения А_min:

3. рабочая фаза В(f) позволяет судить о выполнении требований к ее линейности в пределах ПП (если такие имеются).

Расчет нормированных характеристик рабочего ослабления а(ω) и рабочей фазы в(ω) фнч производим, пользуясь следующими соотношениями:

А(Ω) = 20lg | 1/T(j Ω) |

B(Ω) = arg { 1/T(j Ω) }

Зададимся частотами Ω для расчета характеристик. Для фильтров Чебышева с равноволновой характеристикой рабочего ослабления в ПП необходимо выбрать в качестве расчетных частоты экстремумов А(Ω).

Т. к. в ПН зависимость А(Ω) фильтров Чебышева имеет монотонно нарастающий характер, достаточно убедиться в выполнении условия A(f) A_min лишь на граничной частоте ПН . Поэтому в качестве расчетной выбираем в ПН одну частоту Ω = Ω₃. Расчет В(Ω) производится на тех же частотах, что и расчет А(Ω).

Для преобразования нормированных А(Ω) и В(Ω) в соответствующие характеристики и B(f) ФНЧ необходимо расчитать значения денормированных и преобразованных частот, соответствующие нормированным частотам Ω ФНЧ .

Для ФНЧ используем преобразование частоты и ее денормирование по следующим формулам:

f = f₂ Ω

Т.к. фильтр Баттерворта, то Ω₀ = 0; 0,25; 0,5; 0,75; 1 в ПН, и Ω = Ω₃ =2.

Выполним преобразование и денормирование частоты по ранее описанным формулам. Соответствующий расчет дает следующие результаты:

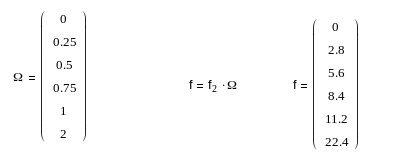
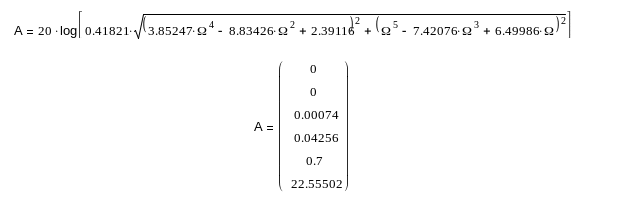
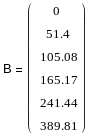
Внесем данные значения в таблицу1:

Таблица 1

Ω	0	0,25	0,5	0,75	1	2,0
f(кГц)	0	2.8	5.6	8.4	11.2	22.4
А(дБ)	0	0	0,00074	0,04256	0,7	22,55502
В(град)	0	51,4	105,08	165,17	241,44	389,81

Построим графики частотных зависимостей рабочего ослабления (рис.7) и рабочей фазы (рис.8) по результатам расчета.

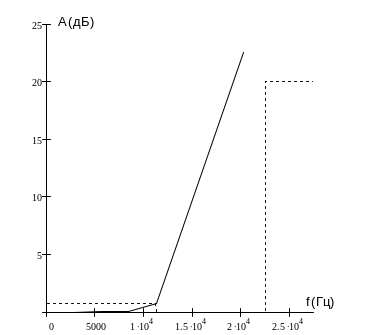
Рис.7 Частотная зависимость рабочего ослабления

Рис.8 Частотная зависимость рабочей фазы

Проверка технических требований по таблице и графикам подтверждает соответствие аппроксимированной Т(р) техническому заданию.