При выборе полинома Баттерворта в качестве аппроксимиующего функция фильтрации определяется выражением:

|φ(jΩ)|²=ε²В²_n(Ω) где:

ε – коэффициент неравномерности рабочего ослабления в полосе пропускания:

при ΔΑ =0,7 дБ

В_n(Ω) = Ωⁿ – полином Баттерворта,

n – порядок полинома Баттерворта, определяемый техническими требованиями к фильтру и являющийся порядком фильтра:

n ≥ 4.57239

Округляя в большую сторону, получим n = 5.

Тогда |φ(jΩ)|²= 0.41821² Ω¹⁰

Перейдем к формированию нормированной рабочей передаточной функции Т(р) по Баттерворту:

|T(jΩ)|² = 1/(1+ 0.41821² Ω¹⁰)

или

где V(p)=(p–p₁)(p–p₂)…(p–p_n) – полином Гурвица, определяемый корнями уравненя 1+ ε² (p/j)²ⁿ=0, лежащими в левой полуплоскости.

Э ти корни определяются соотношением:

Р абочее ослабление получим через рабочую передаточную функцию Т(jΩ)=Т(р)_р=jΩ.

Окончательно получим:

Проверим полученное выражение А(Ω) на частотах Ω₁ = 0, Ω₂ = 1 и

Ω₃. Рабочее ослабление А на первой частоте должно быть равно 0, на второй – ΔА, и на последней А_min.

Расчет подтверждает это:

5.Реализация схемы фнч На данном этапе по найденной ранее функции т(р) необходимо получить схему фнч.

Существует несколько способов реализации электрических фильтров: по Дарлингтону, ускоренный метод реализации симметричных и антиметричных фильтров Попова П.А., реализация по каталогу нормированных схем и т.д. Реализация по Попову основана на формировании функции Z_вх(р) по Т(р). Тогда получение схемы нагруженного фильтра можно свести к реализации двухполюсника путем разложения функции Z_вх(р) в цепную дробь (по Кауэру).

Для каждой пары комплексно – сопряженных корней р(к) полинома V(p) передаточной функции Т(р) (полученной на этапе аппроксимации) составим элементарный множитель Нк :Н_к = (р – р(к))(р – р(к)*) = р² + 2σ_кр + σ_к² + Ω_к²

где р(к) = -σ_к + jΩ_к , р(к)^* = -σ_к - jΩ_к .

С формируем полином Мz(p) как произведение элементарных сомножителей H_к с нечетными индексами

С формируем полином Nz(p) как произведение элементарных сомножителей Н_к с четными индексами:

Определим Kz из условия

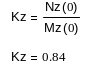
Составим функцию Zвх (р) по формуле:

Разложим полученную функцию в цепную дробь по Кауэру

и построим нормированную схему правой половины фильтра (рис.1)

Рис.1 Нормированная схема правой половины фильтра

Р еализуем левую половину фильтра в соответствии с условием симметрии Z _вых1 = Z_вх2 (рис.2)

Рис.2 Нормированная схема левой половины фильтра

После объединения левой и правой половин и замены источника тока на эквивалентный источник напряжения, получим полную нормированную схему фильтра (рис.3).

Рис.3 Полная нормированная схема фильтра

l₁ = l_3л = 0.5191475 с₂ = с_2л = 1.3591457

l₃ = l_1л + l_1пр = 1.6799965 с₄ = с_2пр = 1.3591457

l₅ = l_3пр = 0.5191475

Получим дуальную схему фильтра (рис.4)

Рис.4 Дуальная схема фильтра

c₁ = c_3л = 0.5191475 l₂ = l_2л = 1.3591457

c₃ = c_1л + c_1пр = 1.6799965 l₄ = l_2пр = 1.3591457

c₅ = c_3пр =0.5191475 r₁ = r₂ = 1