5.1.25 Звездочки приводных роликовых цепей.

Рис.2.Схема звёздочки

5.1.26. Определяем диаметр выходного конца вала (диаметр отверстия в ступице звездочки).

d_в1=36 мм.

d_в2=

Для валов из конструкционных углеродистых сталей ≤15-20 МПа.

Принимаем =18 МПа.

d_в2= =63,16 мм.

Принимаем d_в2=63 мм.

5.1.27 Диаметр делительной окружности d, мм.

d₁= = =24,57мм;

d ₂= = =267,14 мм.

Где d1-диаметр ведущей звездочки;

d ₂- Диаметр окружности выступов d _с, мм.

d _с1=t·(0,5+ctg )=19,5·(0,5+ctg )=24,7 мм;

d _с2=t·(0,5+ctg )=19,5·(0,5+ctg )=21,08 мм.

5.1.28 Диаметр окружности впадин d_i, мм.

d_i= d₁-2r ;

где r-радиус впадин, мм;

r=0,5025· d₁+0,05

d₁-диаметр ролика, мм. d₁=11,91 мм.

r=0,5025· 11,91+0,05=6,03 мм.

d_i1=24,57-2·6,03=12,51 мм;

d_i2=267,14-2·6,03=255,08 мм.

5.1.29 Ширина зуба звездочки b, мм.

b =0,93·В_ВН-0,15

где В_ВН-внутренняя ширина цепи, мм. В_ВН=12,7 мм.

b =0,93·12,7-0,15=11,661 мм.

5.1.30 Расстояние от вершины зуба до линии центров дуг закругления h, мм.

h =0,8· d₁=0,8·11,91=9,528 мм.

5.1.31 Радиус закругления зуба R, мм.

R=1,7· d₁=1,7·11,91=20,247 мм.

5.1.32 Диаметр ступицы.

d_ст=1,5-2,0d_в

где d_в-диаметр выходного конца вала, мм

d_ст=1,7·63,16 =107.372мм

5.1.33 Длина ступицы L, мм.

L=(1,6-1,8)· d_в

L=1,7·63,16 =107.372мм;

5.1.34 Диаметр обода наибольший d₀, мм.

d₀=t·ctg180/z-1,3b

d₀=19,5·7,9-1,3·11,661 =138.89мм

5.1.35 Толщина обода δ₀, мм.

δ₀=0,6· b=0,6·11,661=6,996 мм.

5.2 Расчет закрытой зубчатой передачи. U_з.п.=2

Исходные данные:

L=2,5 года. Зубчатые колеса расположены у середины пролета. Вращающий момент на валу шестерни Т₂= кН·м; вращающий момент на валу шестерни Т₁= кН·м; частота вращения n2 = 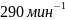, n1 = 487,5 ; передаточное отношение i=3,362.

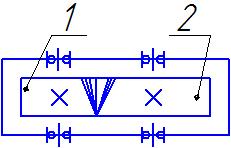
Рисунок . –схема передачи:

1-шестерня; 2-колесо.

5.2.1 Выбор материала для изготовления зубчатых колес.

Материал колеса: Сталь 45 термообработка-улучшение. Твердость поверхности НВ=235…262

НВ₁= =248,5

Предел прочности σ_в = 780 МПа, предел текучести σ_т = 540 МПа;

Материал шестерни: Сталь 40, термообработка-нормализация. Твердость поверхности НВ₂=179…207

НВ₂= =193

Предел прочности σ_в = 580 МПа, предел текучести σ_т = 340 МПа.

5.2.2 Допускаемые контактные напряжения [σ_Н]₂, МПа.

[σ_Н]₂ =

σ_H^o_lim2 – предел контактной выносливости зубьев, МПа;

S_H – коэффициент запаса прочности.

Для зубчатых колес с поверхностным упрочнением зубьев- S_H=1,2

σ_H^o_lim2 =2HB+70=2·193+70=456 МПа

[σ_Н]₂ = = 380 МПа

5.2.3 Допускаемые напряжения изгиба [σ_F], МПа:

[σ_F]=

σ_F⁰_lim1 – предел выносливости зубьев при изгибе при «отнулевом» (пульсирующем) цикле нагружений, МПа;

S_F – коэффициент запаса прочности.

σ_F⁰_lim1= 1,75НВ=1,75·248,5=434,9 МПа,

S_F =1,7

σ_F⁰_lim2=1,75·193=337,7 МПа

[σ_F]₁= = 255,82 МПа

[σ_F]₂= = 198,64 МПа

5.2.4 Расчетная нагрузка с учетом режима работы зубчатых передач.

5.2.5Определяем расчетный вращающий момент на контактную прочность, Т̒_Рн, Н·мм .

Т̒_Рн=Т_maxk_НДk^̒_H= ·1·1,25=0,7113 Н·мм

где Т_max – наибольший момент нормально протекающего технологического процесса, Н·мм; Т_max=Т₂

k_НД –коэффициенты контактной и изгибной долговечности. Принимаем k_НД=1;

k^̒_H –коэффициенты нагрузки.

Принимаем k_НД=1 ввиду наложенного ограничения.

k^̒_H= k^̒_Hv× k^̒_Hβ× k^̒_Hα=1,1·1,036·1,1=1,25

где k^̒_Hv – коэффициенты динамичности;

k^̒_Hβ – коэффициенты концентрации нагрузки;

k^̒_Hα– коэффициенты неравномерности распределения нагрузки между зубьями.

Коэффициент неравномерности распределения нагрузки между зубьями k^̒_Hα=1,1 при ориентировочной окружной скорости:

V̒= · = · =2,3 м/с

где Ψ_ва-коэффициент ширины колеса по межосевому расстоянию;

-коэффициент, учитывающий способ термической обработки.

Обработка У₁+Н₂(У₂). Принимаем =15.

k_Нβ= k^о_Нβ(1-X)+X≥1,1

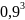k_Нβ= 1,24·(1-0,85)+0,85=1,036. Принимаем k_Нβ=1,1. Начальный коэффициент нагрузки k^о_Нβ=1,24 при =Ψ_ва· =0,4· =0,6 , ≤350. Коэффициент режима Х=0,2+ ·0,8=0,85 согласно графику нагрузки.

Коэффициент динамичности k^̒_Hv=1,10 при окружной скорости V̒=2,29 м/с, ≤350 и 9-ой степени точности изготовления.

5.2.4 Определяем расчетный вращающий момент на изгибную прочность Т̒_PF, Н·мм.

Т̒_PF=Т_maxk_FДk^̒_F= ·1·1,309=0,7448 Н·мм

где Т_max – наибольший момент нормально протекающего технологического процесса, Н·мм;

k_FД –коэффициенты контактной и изгибной долговечности. Принимаем k_FД=1;

k^̒_F –коэффициенты нагрузки.

Принимаем k_FД=1 ввиду наложенного ограничения.

k^̒_F= k^̒_Fv× k^̒_Fβ× k^̒_Fα=1,19·1,1·1=1,309

где k^̒_Fv – коэффициент динамичности;

k^̒_Fβ – коэффициент концентрации нагрузки;

k^̒_Fα – коэффициент неравномерности распределения нагрузки между зубьями.

k^̒_Fα=1 при 9-ой степени прочности.

k^̒_Fβ = k^о_Fβ(1-X)+X≥1,1

k^̒_Fβ = 1,24·(1-0,85)+0,85=1,036. Принимаем k^̒_Fβ =1,1

Начальный коэффициент нагрузки k^о_Fβ=1,24 при =Ψ_ва· =0,4· =0,6, ≤350. Коэффициент режима Х=0,2+ ·0,8=0,85 согласно графику нагрузки.

k^̒_Fv=1,19 при окружной скорости V̒=2,3 м/с, ≤350 и 9-ой степени точности изготовления.

5.3 Проектный расчет передач на контактную прочность.

5.3.1 Межосевое расстояние a̒_ω , мм.

a̒_ω – главный параметр, обеспечивающий контактную прочность

a̒_ω= (u+1)

где К- расчетный коэффициент: для косозубых передач К=270

a̒_ω =(2+1)× = 182,31 мм

По ГОСТ 2185-66 принимаем a_ω=180 м

5.3.2 Ширина венца колеса b₂ ,мм

b₂=ψ_ва· a_ω=0,4·180=72 мм

5.3.3 Ширина венца шестерни b₁ ,мм

b₁=1,12·b₂=1,12·72=80,64 мм

Принимаем b₁=81 мм.

5.3.4 Модуль зацепления нормальный m_H , мм

m_H=(0,01…0,02)a_ω=(0,01…0,02)·180=1,8…3,6 мм

Принимаем m_H=3 мм из единого ряда

5.3.5 Суммарное число зубьев Z_∑

Угол наклона зубьев β_min=arcsin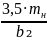 = arcsin =8,39⁰

Z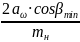_∑= = =119

5.3.6 число зубьев шестерни Z₁

Z₁= >Z_1min= =39,6

Принимаем Z₁=40

Z_1min= = =17,56

5.3.7 Число зубьев колеса Z₂

Z₂= Z_∑- Z₁=119-40=79

5.3.8 Уточнение угла наклона зубьев β,град

β=arccos =arccos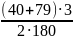 = arcos(0,99)=7⁰4´

5.3.9 Фактическое передаточное число U_ф

U_ф

5.3.10 Диаметры делительной окружности шестерни d₁ и колесаd₂ ,мм

d₁= = =121,007 мм

d₂= = =238,99 мм

a_ω=0,5·(d₁+d₂)=0,5·(121,007+238,99)=179,99 мм=180 мм.

5.3.11 Диаметры вершин зубьев шестерни d_а1 и колеса d_а2 , мм

при х₁=х₂=0

d_а1=d₁+2 ·m_H=121,007+2·3=127,007 мм

d_а2=d₂+2·m_H=238,99+2·3=244,99 мм

5.3.12 Диаметры впадин зубьев шестерни d_f1 и колеса d_f2 ,мм.

при х₁=х₂=0

d_f1=d₁-2,5·m_H=121,007-2,5·3=113,507 мм

d_f2=d₂-2,5·m_H=238,99-2,5·3=231,49 мм

5.3.13 Окружная скорость в зацеплении V при частоте вращения валов n₁ и n₂ ,мин^-1.

n₁=487,5 мин^-1, n₂= = =246,84мин ^-1

V₁=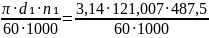 =3,09 м/с

V₂= = = 3,09 м/с

5.4 Силовой расчет цилиндрических зубчатых передач.

5.4.1 окружная сила F_t,кН.

F_t= = =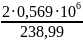4,761 кН

5.4.2 Радиальная сила F_r,кН.

F_r= F_t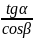 =4,761· =1,75 кН

5.4.3 Осевая сила F_а, кН.

F_а= F_ttgβ=4,761·tg7⁰4´=0,62 кН

5.5 Проверочный расчет на контактную прочность.

Проверочный расчет на контактную прочность проводят по условию

σ_н = К· · ≤[σ_H]

Уточняют расчетный момент, Т_рн, Н·мм по коэффициенту нагрузки К_н

Т_рн=Т₂·К_Нд·К_н= · ·1·1,25=0,711·10⁶ Н·мм

К_н=К_Нα·К_Нβ·К_НV=1,1·1,1·1,0,36=1,25

К_Нα=1,1 при V=3,09 м/с ;С_v=15 и 9^ой степени точности.

К_НV=1,04 при V=3,09 м/с; ≤350 9^ой степени точности

σ_н = 270· · = 387,28 МПа

Степень загруженности ·100%=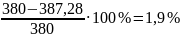

Перегрузка составляет 1,9% допускается до 10%. Контактная прочность передачи обеспечена.

5.6 Проверочный расчет зубьев на изгиб.

Проверочный расчет зубьев на изгиб проводят по условию

σ_F= ·F_t·К_Fд·К_F≤[σ_F]

для шестерни Y_F1=3,70 при Z_V1= = =41,02 методом линейного интерполирования и х₁=0

Для колеса Y_F2=3,6 при Z_V2= = =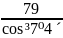81 и х₂=0

Коэффициент Y_β1=1 - =1- =0,99; Y_β1= Y_β2

К_F= К_Fα· К_Fβ· К_FV=1·1,1·1,19=1,309

σ_F1= ·4761·1·1,309=105,69 МПа

σ_F2=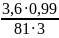 ·4761·1·1,309=91,4 МПа

[σ_F]₁= 255,82 МПа

[σ_F]₂= 198,64МПа

Условие прочности на изгиб для шестерни и колеса выполняются.

5.7 Проверка прочности зубьев колес при перегрузках

5.7.1 Проверка на контактную прочность

σ_Hmax=σ_H· ≤[ σ_Hmax]

Для принятого электродвигателя

Т_пуск=1,4·Т=1,4· · =0,797·10⁶ Н·мм

[ σ_Hmax]=2,8σ_Т=2,8·340=952 МПа

σ_Hmax=387,28 · = 542 МПа

Условие прочности выполняется.

5.7.2 проверка статической прочности зубьев на изгиб

σ_Fmax=σ_F· ≤[ σ_Fmax]

σ_Fmax1= 105,69· = 148,04 МПа

σ_Fmax2=91,4· =128,02 МПа

[σ_Fmax]₁=2,7· =2,7·248,5=670,95 МПа

[σ_Fmax]₂=2,7· =2,7·193=521,1 МПа

Условие прочности выполняется