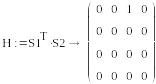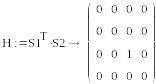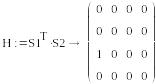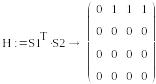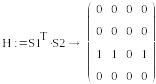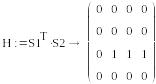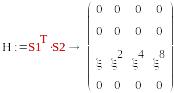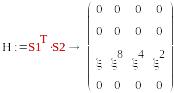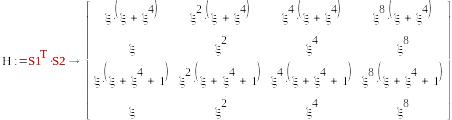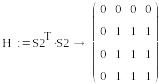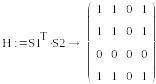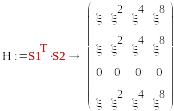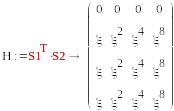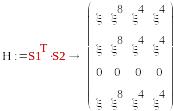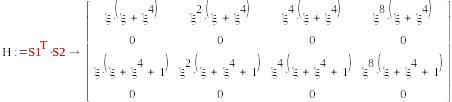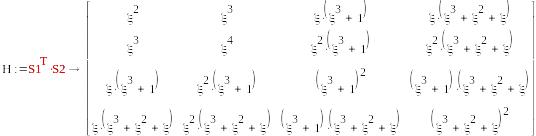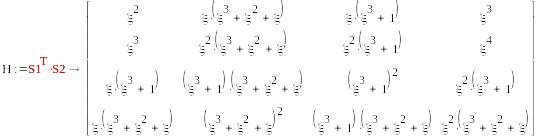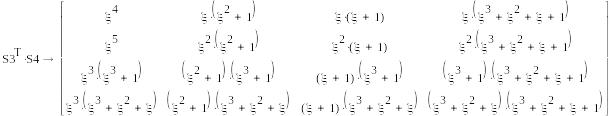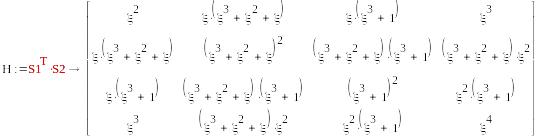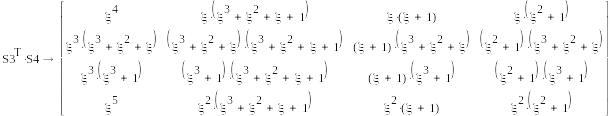Список использованной литературы

1. Айерлэнд, К. Классическое введение в современную теорию чисел / К. Айерлэнд, М. Роузен.– М.: Мир, 1987.– 416 с.

2. Cusick T W, Ding C, Renvall A. Stream Ciphers and Number Theory. Amsterdam: Elsevier, 1998.

3. Whiteman A L. A family of difference sets. Illinois J. Math., 1962, 6: 107-121.

4. Свердлик, М.Б Оптимальные дискретные сигналы / М.Б. Свердлик. – М.: Сов.радио, 1975. – 200 с.

5. D.H. Green and P.R. Green. Modified Jocobi sequences. IEE Proc. Comput. Digit. Tech.,147(4), 2000.

6. Лидл, Р. Конечные поля / Р. Лидл, Нидеррайтер Г. – М.: Мир, 1988.– 820 с.

7. Edemskiy, O. Antonova .About Computation of the Linear Complexity of GeneralizedCyclotomic Sequences with Period pq. Proceedings of 2011 International Workshop on Signal Design and Its Applications in Communications (IWSDA’011). China. 2011, pp. 9-12.

8. Едемский В. А. О линейной сложности двоичных последовательностей на основе классов биквадратичных и шестеричных вычетов. Дискретная математика. 2010 г. Т. 22, вып. 1 . С. 74-82.

9. Едемский, В.А. Синтез двоичных и троичных последовательностей с заданными ограничениями на их характеристики / В.А. Едемский, В. Е. Гантмахер.– Великий Новгород.: НовГУ, 2009.– 189 с.

Приложение 1

Вычисление матриц H.

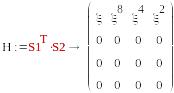
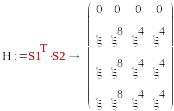
1. 1в*1в S1=(1, 0, 0, 0) , S2=(1,0,0,0)

S1=(1, 0, 0, 0) , S2=(0,0,1,0)

S1=(0, 0, 1, 0) , S2=(0,0,1,0)

S1=(0, 0, 1, 0) , S2=(1,0,0,0)

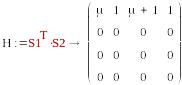
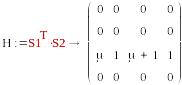
1в*2в S1=(1, 0, 0, 0) , S2=(μ,1,1+μ,1)

S1=(0, 0, 1, 0) , S2=T2=(μ,1,1+μ,1)

1в*3в S1=(1, 0, 0, 0) , S2=T2=(1,1,0 ,1)

S1=(1, 0, 0, 0) , S2=T2=(0,1,1 ,1)

S1=(0, 0, 1, 0) , S2=T2=(1,1,0 ,1)

S1=(0, 0, 1, 0) , S2=T2=(0,1,1 ,1)

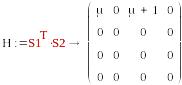
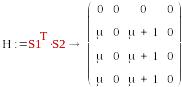
1в*4в S1=(1, 0, 0, 0) , S2=T2=(μ,0,μ+1,0)

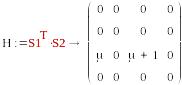
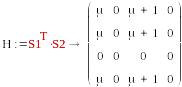
S1=(0, 0, 1, 0) , S2=T2=(μ,0,μ+1,0)

1в*5в S1=(1, 0, 0, 0) , S2=T2=( )
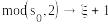
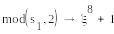		= 1

S1=(0, 0,1, 0) , S2=T2=( )
		==
		=

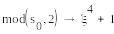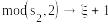
S1=(0, 0,1, 0) , S2=T2=( )
		=
		=

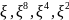S1=(1, 0,0, 0) , S2=T2=( )
		=
		=

2в*2в S1=( μ,1,μ+1,1) , S2=(μ,1,μ+1,1)

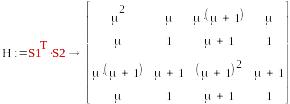
2в*3в S1=( μ,1,μ+1,1) , S2=(1,1,0,1)

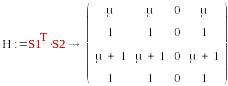
S1=( μ,1,μ+1,1) , S2=(0,1,1,1)

2в*4в S1=( μ,1,μ+1,1) , S2=( μ,0,μ+1,0)

2в*5в S1=( μ,1,μ+1,1), S2=T2=( ), µ=
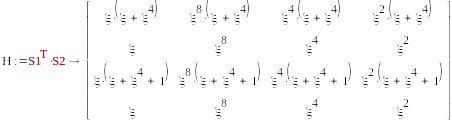
		mod(
		mod(
		mod( ξ+1
		mod( ξ^3+ξ^2+ξ+1

S1=( μ,1,μ+1,1), S2=T2=( )
		mod(
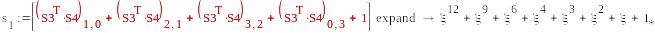
		mod(
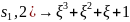
		mod( ξ+1
		mod(

3в*3в S1=(1,1, 0, 1) , S2=( 0,1,1,1)

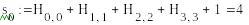
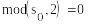
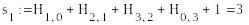
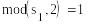
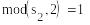
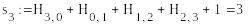
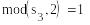
S1=(0,1, 1, 1) , S2=(0,1,1,1)

S1=(1,1, 0, 1) , S2=(1,1,0,1)

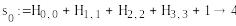
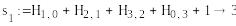
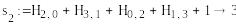
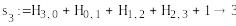
S1=(0,1, 1, 1) , S2=(1,1,0,1)

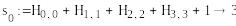
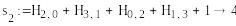
3в*4в S1=(0,1, 1, 1) , S2=( μ,0,μ+1,0)

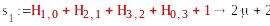
S1=(1,1, 0, 1) , S2=(μ,0,μ+1,0)

3в*5в S1=( 1,1,0,1), S2=T2=( )
		=
		=

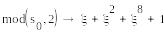
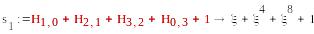
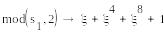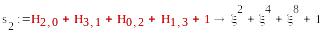
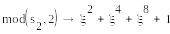
S1=(0,1,1,1), S2=T2=( ),
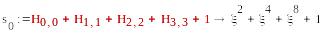
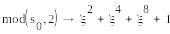		=ξ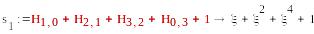
		=
		=

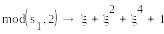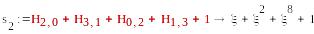
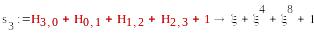
S1=(0,1,1,1), S2=T2=( ),

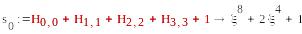
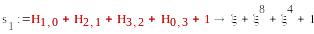
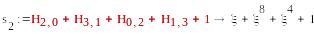
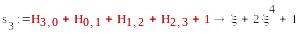
S1=(1,1,0,1), S2=T2=( ),
		=
		=

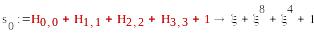
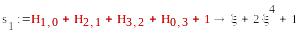
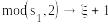
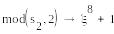
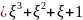
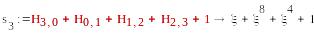
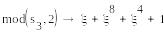4в*4в S1=(μ,0,μ+1,0), S2=(μ,0,μ+1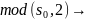,0)
		0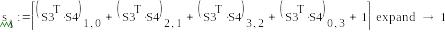

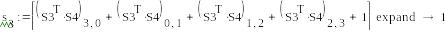
4в*5в S1=(μ,0,μ+1,0) , S2=( )

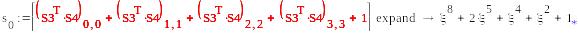
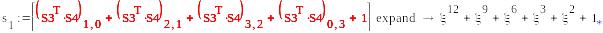
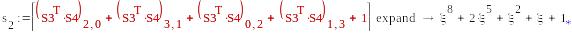
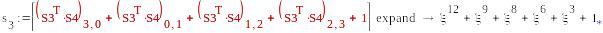
S1=( μ,0,μ+1,0) , S2=( )

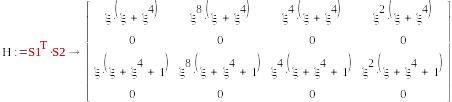
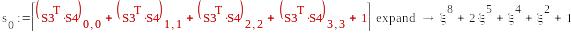
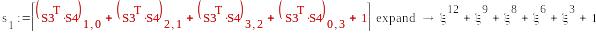
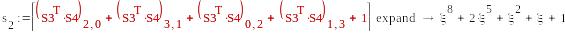
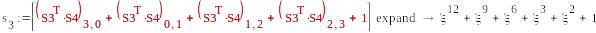
5а*5а ), )
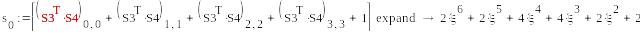
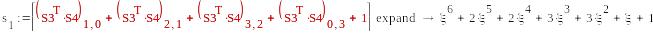
		0
		0

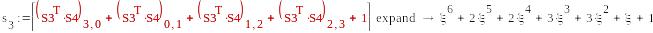
5а*5b ), )
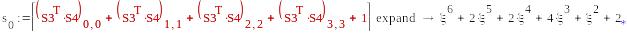
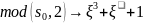
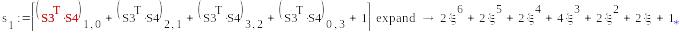
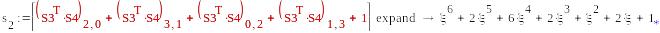
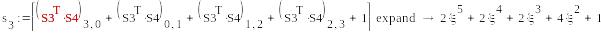
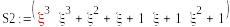
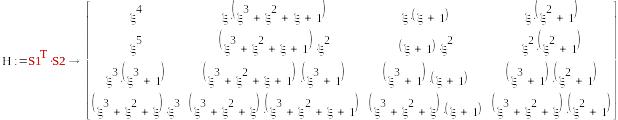
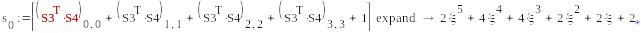
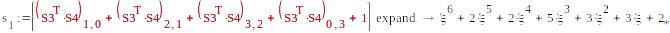
		1

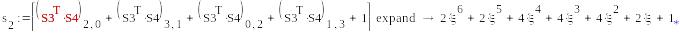
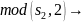		1
		1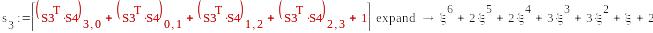

5a*5d

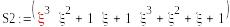
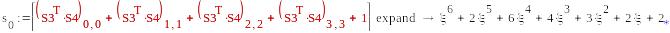
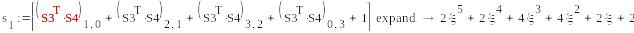
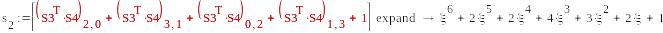
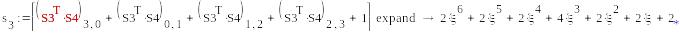
5b*5b
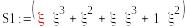
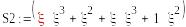
		0
		mod(s1,2) 0

5b*5c
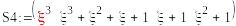
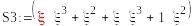
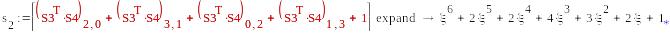
		+^3
		^3

5b*5d

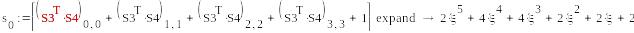
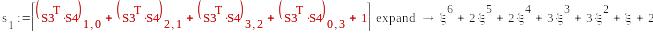
5c*5c
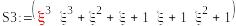
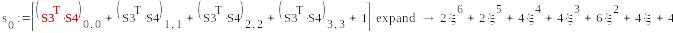
		mod(s0,2)0
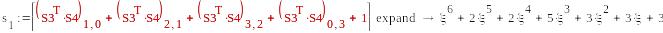
		0
		mod(s2,2)1
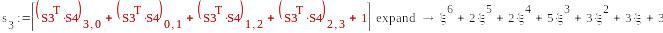
		mod(s3,2)0

5c*5d

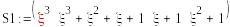
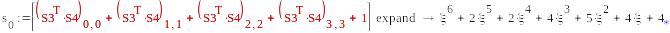
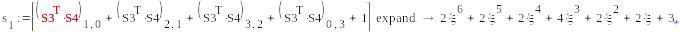
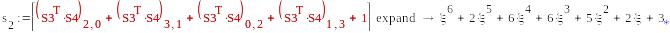
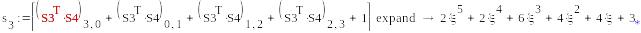
5d*5d
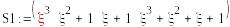
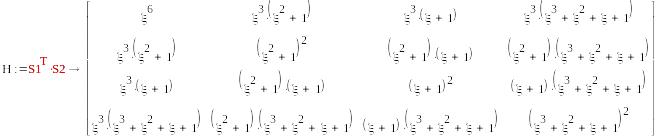
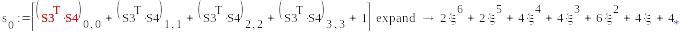
		mod(s0,2)0
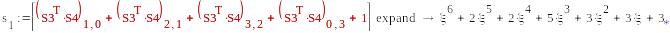
		mod(s1,2)0
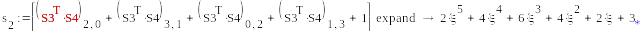
		mod(s2,2)1
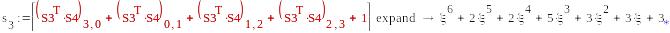
		mod(s3,2)0