
- •Министерство образования и науки Российской федерации
- •«Новгородский государственный университет имени Ярослава мудрого»
- •Содержание
- •Перечень сокращений, символов и специальных терминов
- •Введение
- •Обобщеные циклотомические оследовательности уитмена
- •Основные опрЕделения
- •1.3 Обобщенные циклотомические классы по модулю
- •Вычисление линейной сложности последовательностей уитмена четвертого порядка
- •Список использованной литературы
- •Приложение 1
Вычисление линейной сложности последовательностей уитмена четвертого порядка
Пусть
последовательность Уитмена четвертого
порядка, то есть
 ,
тогда, согласно лемме 1.1, она формируется
по правилу:
,
тогда, согласно лемме 1.1, она формируется
по правилу:
 (2.1)
(2.1)
Заметим, что правило
(2.1) задает последовательность Уитмена
только тогда, когда
 .
Здесь откажемся
от этого предположения и рассмотрим
общий случай. Таким образом, по теореме
1.1, имеем
.
Здесь откажемся
от этого предположения и рассмотрим
общий случай. Таким образом, по теореме
1.1, имеем
 .
(2.2)
.
(2.2)
Как и в [7] из формулы (2.2) получаем следующее утверждение.
Лемма 2.1. Если
последовательность
определена по правилу (2.1), тогда для имеем
имеем

Следствие 2.1.
Значение
многочлена
 последовательности Уитмена постоянно,
когда
принадлежит
обобщенным циклотомическим классам
Уитмена, множествам
последовательности Уитмена постоянно,
когда
принадлежит
обобщенным циклотомическим классам
Уитмена, множествам
 .Пусть
.Пусть
 ,
когда
,
когда
 .
.
Воспользовавшись формулой (1.7) из леммы 2.1 получаем, что
 , (2.3)
, (2.3)
где
 и
и

Прежде
чем приступить к вычислению ,
введем несколько обозначений. Пусть,
далее,
,
введем несколько обозначений. Пусть,
далее,
 и
и
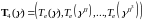 .
Определим матрицу
.
Определим матрицу
 четвертого
порядка следующим образом:
четвертого
порядка следующим образом:
 (*-
транспонирование матрицы).
(*-
транспонирование матрицы).
Лемма
2.2.Если
,
то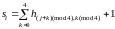 или
или
 (2.4)
(2.4)
Данная формула следует непосредственно из леммы 2.1.
Таким образом,
фактически, для расчета линейной
сложности циклотомических последовательностей
Уитмена достаточно рассчитать матрицу
для этого случая. В [9] были найдены
значения
 для
для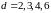 и частично для
и частично для .
В частности, если
,
то всегда справедливо разложение
.
В частности, если
,
то всегда справедливо разложение
 ,
,
 -
целые числа и
-
целые числа и
 ,
посредством которого и находятся
значения
,
посредством которого и находятся
значения
 .
Согласно [9] имеют место следующие
соотношение:
.
Согласно [9] имеют место следующие
соотношение:
1.
 или
или ,
если
,
если
 ,
то есть
,
то есть
 и
и
 ,
где
,
где
 - дискретный логарифм 2 по основанию
по модулю
;
- дискретный логарифм 2 по основанию
по модулю
;
2.
![]() ,
где
,
где
 –
корень уравнения
–
корень уравнения
 ,
если
,
если
 ,
то есть
и
,
то есть
и
 ;
;
3.
 или
или
 ,
если
,
если
![]() ,
то есть
,
то есть
 и
;
и
;
4. ,
если
,
если
 ,
то есть
и
;
,
то есть
и
;
5.  или
или ,
если
,
если
 ,
где
,
где
 - корень пятнадцатой степени из единицы
в расширении поля
,
при этом он удовлетворяют уравнению
- корень пятнадцатой степени из единицы
в расширении поля
,
при этом он удовлетворяют уравнению
 .
В первом варианте
.
В первом варианте
 ,
а во втором
,
а во втором
 .
Отметим, что
.
Отметим, что
 будет корнем 3 из единицы, поэтому можно
считать без нарушения общности, что
будет корнем 3 из единицы, поэтому можно
считать без нарушения общности, что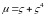 .
.
Далее, так как
справедливо разложение
 ,
то для
,
то для возможны
два варианта:
возможны
два варианта:
1. - корень первого множителя, тогда является корнем пятой степени из единицы;
2. -корень второго множителя, тогда он первообразный корень пятнадцатой степени из 1.
Для удобства
вычислений обозначим через
именно корень пятнадцатой степени из
единицы и, в первом случае заменим ς
на .
Таким образом, мы имеем 4 варианта:
.
Таким образом, мы имеем 4 варианта:
5a. ,
здесь
;
,
здесь
;
5b. ,
здесь
,
здесь
 ;
;
5c. ,
здесь
;
,
здесь
;
5d. ,
здесь
.
,
здесь
.
При этом выполняются
соотношения: ,
,
 ,
,
 и так далее.
и так далее.
Формулы для аналогичны.
аналогичны.
Сразу же заметим,
что в первых четырех вариантах ,
то есть
,
то есть
 ,
а в пятом
,
а в пятом
 ,
тогда
,
тогда
 .
Аналогично, если для q
имеет место
один из первых четырех вариантов, то
.
Аналогично, если для q
имеет место
один из первых четырех вариантов, то
 ,
а в пятом -
,
а в пятом -
 .
.
Приведем несколько значений простых чисел, удовлетворяющих условиям каждого из вариантов:
 13,
353,593;
13,
353,593;17, 929;
73, 89, 233;
41, 313, 761;
5,13, 61;
5a) 13, 29,61;
5b) 397,1069;
5c) 5, 37, 53;
5d) 277, 1093.
Введем дополнительно
следующие обозначения. Пусть
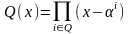 ,
,
 и
и
 .
.
Для получения быстрых и точных расчетов простых чисел была использована следующая программа:
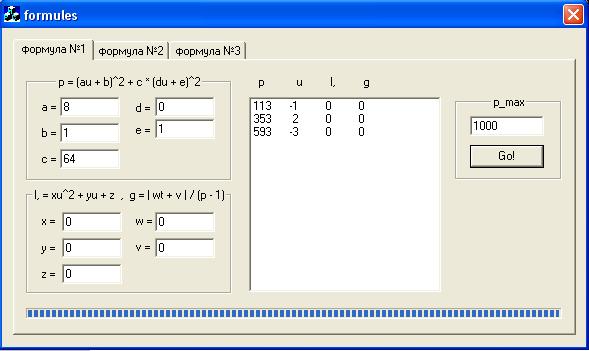
Рисунок 1.Пример
расчета простых чисел для![]() .
.
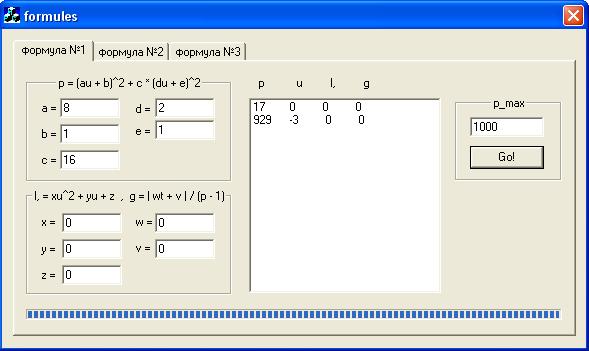
Рисунок 2. Пример расчета простых чисел для .
Для получения
значений
 была использована программа Mathcad.
С помощью неё были рассчитаны матрицы
H:
была использована программа Mathcad.
С помощью неё были рассчитаны матрицы
H:
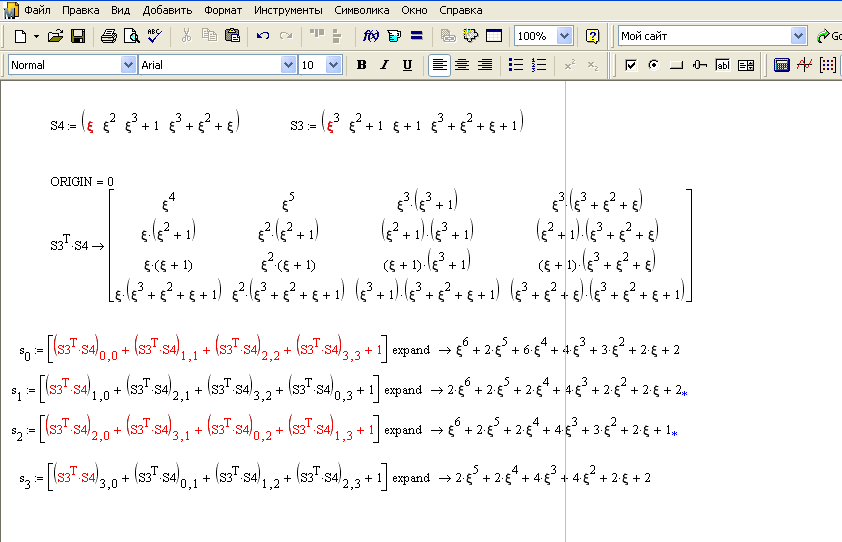
Рисунок 3. Пример расчета матрицы Н в программе Mathcad.
Лемма 2.3. Если
последовательность X
задана правилом (2.1) и
, ,то
,то
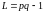 и
и
 .
.
Доказательство.
Согласно
приложению ,
а по условию леммы
и
,
тогда согласно формуле (2.3)
,
а по формуле
.
,
а по условию леммы
и
,
тогда согласно формуле (2.3)
,
а по формуле
.
Таблица 1 — Численные примеры для леммы 2.3.
p |
Q |
N |
L |
p |
Q |
N |
L |
17 |
13 |
221 |
220 |
17 |
29 |
493 |
492 |
41 |
13 |
533 |
532 |
41 |
29 |
1189 |
1188 |
73 |
61 |
4453 |
4452 |
73 |
13 |
949 |
948 |
89 |
61 |
5429 |
5428 |
89 |
29 |
2581 |
2580 |
Лемма 2.4. Если
последовательность X
задана правилом (2.1) и

 то
то и
и
 .
.
Доказательство.
Согласно
приложению
,
а по условию леммы и
,
тогда согласно формуле (2.3)
и
и
,
тогда согласно формуле (2.3)
и .
.
Таблица 2 — Численные примеры для леммы 2.4.
p |
Q |
N |
L |
p |
q |
N |
L |
5 |
17 |
85 |
64 |
5 |
41 |
205 |
160 |
13 |
17 |
221 |
192 |
13 |
73 |
949 |
864 |
29 |
73 |
2117 |
2016 |
29 |
17 |
493 |
448 |
61 |
41 |
2501 |
2400 |
61 |
17 |
1037 |
960 |
Аналогично предыдущим леммам получаются следующие утверждения:
Лемма 2.5. Если последовательность X задана правилом (2.1), то:
1) для
для
 и
и
 ;
;
2) для
для
 и
и
 ;
;
3)
 для
и
;
для
и
;
4)
 для
для
 и
;
и
;
Таблица 3 — Численные примеры для леммы 2.5.
Вариант |
p |
q |
N |
L |
1 |
17 |
73 |
1241 |
1224 |
|
113 |
41 |
2993 |
1512 |
2 |
113 |
353 |
39889 |
29920 |
|
17 |
929 |
12064 |
15793 |
|
73 |
89 |
4840 |
6497 |
|
41 |
313 |
12833 |
9672 |
3 |
17 |
113 |
1921 |
1008 |
|
41 |
73 |
2993 |
1512 |
|
41 |
89 |
3649 |
1848 |
|
17 |
353 |
6001 |
3168 |
4 |
73 |
113 |
8249 |
2128 |
|
17 |
41 |
697 |
200 |
|
313 |
17 |
5321 |
1264 |
|
89 |
113 |
10057 |
2576 |
Лемма 2.6. Если последовательность X задана правилом (2.1), то:
1).
Если
 ,
то
,
то
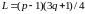 ,
если
,
если
 (A)
и
(A)
и
 (B),
если
(B),
если
 ;
;
2).
Если
 ,
то
,
то
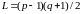 (C),
если
и
(C),
если
и
 (D),
если
.
(D),
если
.
Таблица 3 — Численные примеры для леммы 2.6.
Вариант |
p |
q |
N |
L |
A |
13 |
5 |
65 |
48 |
|
397 |
277 |
109969 |
82368 |
B |
13 |
29 |
377 |
96 |
|
397 |
1069 |
424393 |
106128 |
|
5 |
37 |
185 |
40 |
|
277 |
1093 |
302761 |
75624 |
C |
13 |
277 |
3601 |
1668 |
|
397 |
5 |
1985 |
1188 |
D |
13 |
397 |
5161 |
4764 |
|
5 |
277 |
1385 |
1108 |
Для проверки результатов вычислениябыла использованна программа LCS.exe.:
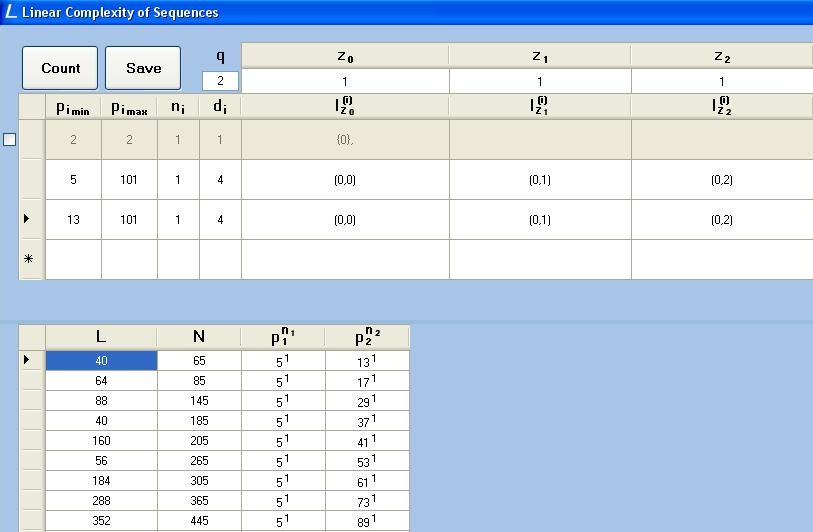
Рисунок 4. Пример работы программы LCS.
ЗАКЛЮЧЕНИЕ
Линейная сложность последовательности является важной характеристикой её качества. Последовательности, обладающие высокой линейной сложностью, важны для криптографических приложений.
В выпускной
квалификационной работе исследована
линейная сложность обощенных
циклотомических последовательностей
Уитмена четвертого порядка с периодом
 .
Определено, при каких значениях параметров
они обладают высокой линейной сложностью.
.
Определено, при каких значениях параметров
они обладают высокой линейной сложностью.
