3.7 Построение системы логических уравнений для описания функций переходов_и_выходов_ц.А._Мура

S(t) = {S(t-1),x(t)}

Y(t) = {S(t-1),x(t)}

T₁= Q1-Q2Q3-X1 V Q1Q2Q3X1-X2 V Q1-Q2-Q3 V -Q1-Q2Q3X1 V –Q1-Q2-Q3

T₂= -Q1Q2Q3X1 V -Q1Q2-Q3 V Q1-Q2Q3-X1 V Q1-Q2-Q3 V Q1Q2-Q3 V Q1Q2-Q3 V-Q1-Q2Q3X1 V –Q1-Q2-Q3

T₃= -Q1-Q2Q3-X1 V –Q1Q2Q3X1 V –Q1Q2-Q3 V-Q1Q2Q3X1X2 V Q1-Q2Q3-X1 V Q1Q2Q3X1X2 V Q1-Q2-Q3 V Q1Q2-Q3 VQ1Q2-Q3-X1 V -Q1Q2Q3X1 V -Q1-Q2-Q3

Y₀ = -Q1-Q2Q3-X1 V –Q1Q2Q3X1

Y₁ = -Q1Q2-Q3 V Q1Q2-Q3 V Q1Q2Q3-X1 V –Q1Q2Q3X1

Y₂ = -Q1Q2Q3X1X2 V Q1-Q2Q3-X1 V Q1Q2Q3X1-X2 V Q1Q2-Q3

Y₃ = Q1-Q2-Q3

Y₄ = Q1Q2-Q3 V Q1Q2Q3

3.8 Построение минимизированной системы логических уравнений ц.А.

T₁= -Q2Q3-X1 V Q1Q2Q3X1-X2 V –Q2-Q3 V –Q1Q2Q3-X1

T₂= -Q1Q2Q3X1 V Q2-Q3 V-Q2Q3-X1 V Q1-Q3 V -Q1-Q2-Q3

T₃= -Q2Q3-X1 V -Q1Q2Q3X1 V Q2-Q3 V -Q1-Q2-Q3X1X2 V Q1Q2Q3X1- X2 V Q1Q2-Q3-X1

Y₀ = -Q1-Q2Q3-X1 V -Q1Q2Q3X1

Y₁ = Q2-Q3 V -Q1-Q2Q3-X1 V -Q1Q2Q3X1

Y₂ = -Q1Q2Q3X1X2 V Q1-Q2Q3-X1 V Q1Q2Q3X1-X2 V Q1Q2-Q3

Y₃ = Q1-Q2-Q3

Y₄ = Q1Q2

3.9 Оптимизация_функций_схемы_ц.А.

Запишем оптимизацию функций схемы Ц.А. Мили в виде таблицы (таблица 3.3).

Таблица 3.3 – Оптимизация функций

	T1	T2	T3	Y0	Y1	Y2	Y3	Y4
k1	+	+	+
k2	+		+			+
k3	+
k4	+
k5		+		+	+
k6		+	+		+
k8		+
k9		+
k13			+
k15			+
k16				+	+
k21						+
k22						+
k24						+
k25							+
k26								+

k₁ = -Q2Q3-X1

k₂ = Q1Q2Q3X1-X2

k₃ = -Q2-Q3

k₄ = -Q1Q2Q3-X1

k₅ = -Q1Q2Q3X1

k₆ = Q2-Q3

k₇ = -Q2Q3-X1

k₈ = Q1-Q3

k₉ = -Q1-Q2-Q3

k₁₀ = -Q2Q3-X1

k₁₁ = -Q1Q2Q3X1

k₁₂ = Q2-Q3

k₁₃ = -Q1-Q2-Q3X1X2

k₁₄ = Q1Q2Q3X1-X2

k₁₅ = Q1Q2-Q3-X1

k₁₆ = -Q1-Q2Q3-X1

k₁₇ = -Q1Q2Q3X1

k₁₈ = -Q2-Q3

k₁₉ = -Q1-Q2Q3-X1

k₂₀ = -Q1Q2Q3X1

k₂₁ = -Q1Q2Q3X1X2

k₂₂ = Q1-Q2Q3-X1

k₂₃ = Q1Q2Q3X1-X2

k₂₄ = Q1Q2-Q3

k₂₅ = Q1-Q2-Q3

k₂₆ = Q1Q2

На основе полученных функций возбуждения и функций выходов построим функциональную схему управляющего автомата Мура (рисунок 3.4).

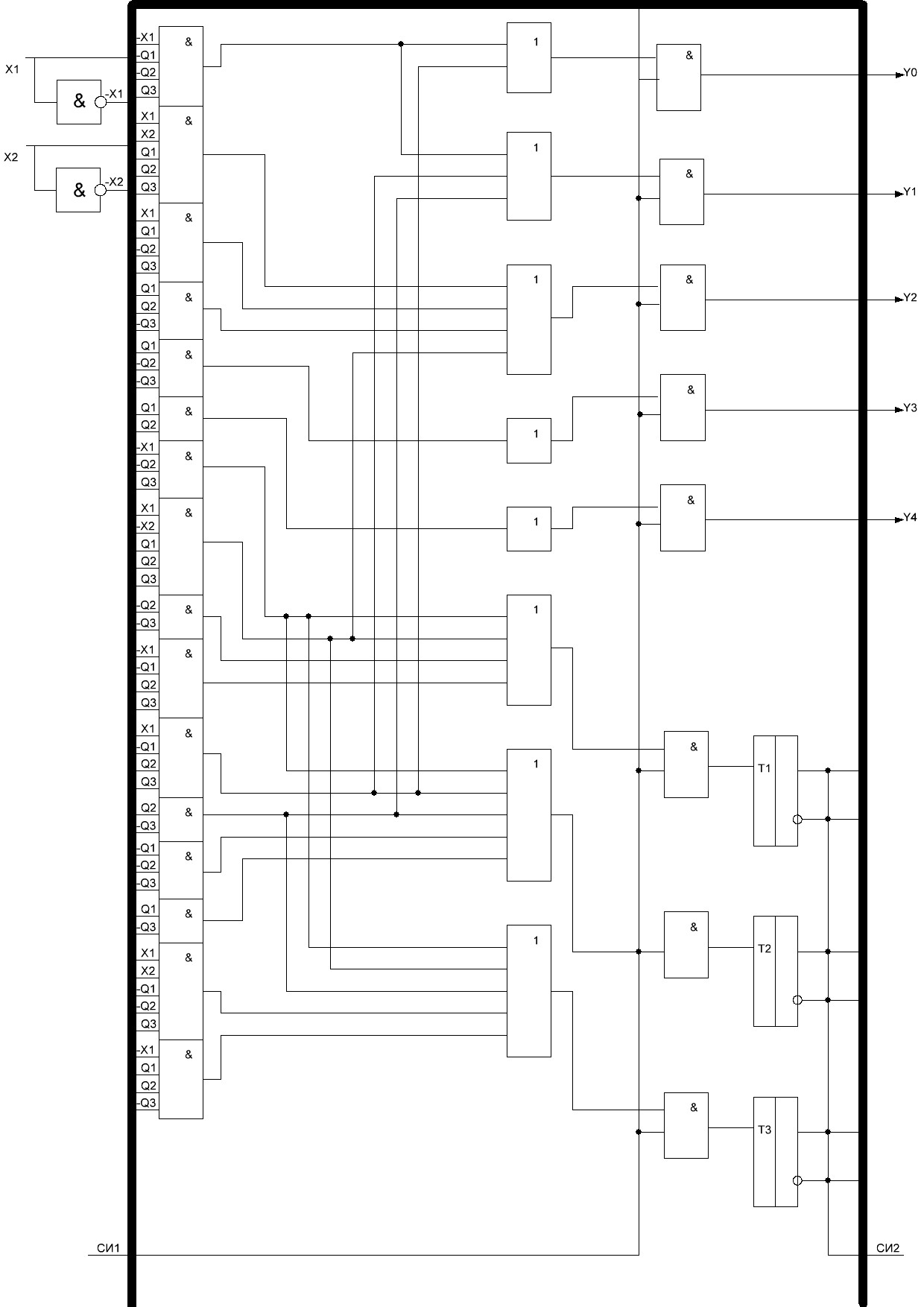
Рисунок 3.4 - Функциональная схема управляющего автомата Мура