5. Методики выполнения курсовой работы
где q – критерий близости модели и объекта, называемый невязкой модели; n –количество экспериментальных данных.
Задача построения линейной модели сводится к минимизации функции невязки следующего вида:
В качестве нелинейных регрессионных моделей чаще всего используются полиномы разной степени:
4. Проверка адекватности структуры модели. Об адекватности структуры модели можно судить по коэффициенту корреляции r или корреляционному отношению η, гистограмме распределения остатков и содержательному анализу остатков модели.
Коэффициент
корреляции r
характеризует
степень тесноты линейной связи между
и приближенное
значение r
определяется
по формуле
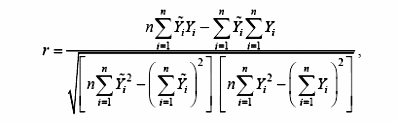(1)
где n – число экспериментальных данных. Коэффициент корреляции изменяется от –1 до +1.
Корреляционное отношение η характеризует степень тесноты нелинейной связи между переменными и рассчитывается по формуле
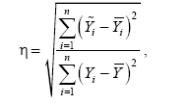(2)
где
–
текущее значение параметра Y,
вычисленное по математической модели;
Yi
– текущее
значение, полученное на объекте;
– выборочное
среднее значение,
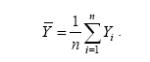(3)
Корреляционное отношение изменяется от 0 до +1.
Следует иметь в
виду, что коэффициент корреляции является
частным случаем корреляционного
отношения и используется обычно только
при исследовании линейных моделей.
Диапазон изменения коэффициента
корреляции
(корреляционного
отношения) указывает на корреляцию
(связь) между
Гистограмма распределения остатков модели строится следующим образом. Весь диапазон изменения остатков (от минимального из остатков до максимального) разбивается на несколько равных интервалов, или поддиапазонов (обычно от 6 до 20), которые откладываются на оси абсцисс. Далее на оси ординат отмечается число попаданий остатка в каждый интервал, или поддиапазон. Число попаданий ошибки можно откладывать как в натуральных показателях, так и в процентном соотношении. При адекватности модели реальному объекту гистограмма распределения приобретает колоколообразный вид, при неадекватности модели она имеет несимметричный характер или второй горб (рисунок 2).
Рисунок 2. Гистограмма распределения остатков:
а – при адекватности модели объекту управления;
б – при неадекватности модели объекту управления
Содержательный анализ остатков модели состоит в построении
распределения остатков модели в зависимости от времени t, от входного параметра X, выходного параметра Y. Графики возможных зависимостей остатков (ошибки) модели от вектора входных параметров X представлен на рисунке 3.
Попадание большинства данных в горизонтальную полосу свидетельствует о том, что наши предположения оправданы, то есть модель адекватна объекту управления. Графики для случаев неадекватности модели объекту управления имеют вид, аналогичный рисунке 3, б–г.
Рисунок 3. Графики зависимости остатков от t: а – эффект времени не влияет на ошибку;
б – дисперсия непостоянна, необходимо использование взвешенного метода наименьших квадратов; в – следует включить в модель линейный член; г – необходимо включить
в модель линейный и квадратичный члены
Графики остатков по каждой из независимых переменных x строят и анализируют соответствующим образом.
Большой интерес при исследовании остатков могут представлять выбросы, т.е. значительные отклонения параметров от установленного закона распределения. С точки зрения получения устойчивых средних значений выбросы за зону шириной ±3σ рекомендуется не учитывать.
Окончательное суждение об адекватности модели принимают на основании анализа коэффициента корреляции, гистограммы распределения и содержательного анализа остатков.