3. Прохождение случайного сигнала через динамическую систему

Рассмотрим динамическую систему (рисунок 2.15) с передаточной функцией W(p) и функцией веса (t)

x₁(t)

W(p)

x₂(t)

Рисунок 2.15 – Линейная динамическая система

На входе системы действует случайный сигнал x₁(t) с корреляционной функцией R₁(t, t₁).

На основании формулы свертки [7, стр. 183, формула (7.44)] выходной сигнал x₂(t)

x₂(t)= . (2.39)

Рассматривая в этой формуле математические ожидания, имеем

(2.40)

Для получения корреляционной функции на выходе запишем исходную формулу для центрированных значений и для двух моментов времени:

(2.41)

После перемножения получим

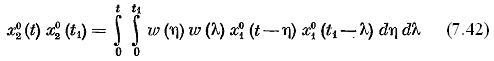
. (2.42)

Далее, переходя к математическому ожиданию, можно найти корреляционную функцию

(2.43)

Для определения дисперсии на выходе D₂(t) в формуле (2.43) следует положить t= t_1. Тогда

. (2.44)

В случае использования канонического разложения случайной функции

(2.45)

выходная величина может быть представлена в виде

, (2.46)

г де определяется формулой (2.40), а координатные функции

. (2.47)

Корреляционная функция выходного сигнала

, (2.48)

а дисперсия

. (2.49)

Для нахождения математического ожидания и координатных функций y_v(t) в соответствии с выражениями (2.40) и (2.47) могут использоваться различные методы построения переходных процессов.

В случае, когда на выходе (рисунок 2.15) действует случайный стационарный процесс, корреляционная функция R₁(t, t₁) = R₁( ) зависит только от сдвига = t₁- t. Однако на выходе линейной системы процесс некоторое время после включения будет устанавливаться и не будет стационарным. Корреляционная функция на выходе может быть получена из общего выражения (2.43):

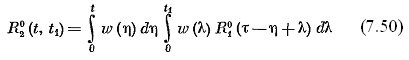
, (2.50)

а дисперсия – из (2.44):

. (2.51)

Если рассматриваемая система устойчива, то R (t, t₁) и D₂(t) стремятся к некоторым пределам, которые определяют стационарный процесс на выходе. Они могут быть найдены из (2.50) и (2.51), если положить и .

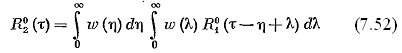Т огда

, (2.52)

. (2.53)

Пусть, например, на выходе интегрирующего звена с передаточной функцией W(p)=k/p и функция веса (t)=k действует белый шум с (2.40), дисперсия на выходе будет

,

т.е. дисперсия растет пропорционально времени. Нетрудно видеть, что , так как звено не является устойчивым, а находится на границе устойчивости (нейтрально-устойчивый объект).

Для расчета установившегося стационарного процесса на выходе системы (рисунок 2.15) более удобно исходить из известной спектральной плотности на выходе S₁(ω). Тогда можно легко найти спектральную плотность S₂(w) выходного сигнала. Действительно, по определению, спектральная плотность на выходе связана с изображением Фурье F₁(jw) случайной величины x₁(t) соотношением:

.

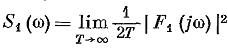Это же соотношение имеет место и для выходного сигнала:

.

В линейной системе изображения Фурье F₁(jω) и F₂(jω) связаны между собой посредством частотной передаточной функции:

.

Отсюда можно найти

и ли

. (2.54)

Таким образом, спектральная плотность выходной величины может быть получена умножением спектральной плотности выходной величины на квадрат модуля частотной передаточной функции линейной системы. Отметим, что приведенное выше доказательство, вообще говоря, не является строгим, так как существование стационарного случайного процесса на выходе не доказано.

При известной спектральной плотности S₂(ω) выходной величины может быть найдена корреляционная функция R₂( ) по преобразованию Фурье.

Получим выражение (2.54) более строго. Для этого используем формулу (2.52). Так как в реальных системах весовая функция тождественно равна нулю при t<0, то нижние пределы интегрирования можно положить равными - . Полагая, что на выходе действует центрированный процесс ( =0) и R₁( )=R ( ), имеем

. (2.55)

Н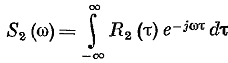 айдем теперь спектральную плотность для выходного сигнала. Она связана с корреляционной функцией соотношением:

. (2.56)

Подставляя в последнюю формулу значение корреляционной функции из (2.55), получаем

(2.56)

.

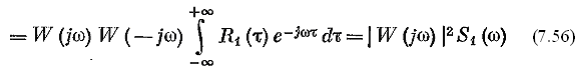
Последнее выражение совпадает с (2.54), что и требовалось доказать.

Для нахождения дисперсии, или среднего квадрата выходной величины, необходимо проинтегрировать по всем частотам спектральную плотность:

. (2.57)

Отметим, что закон распределения для случайной величины может, вообще говоря, меняться при прохождении ее через линейную систему. Однако в случае, если на входе линейной системы имеется нормальное распределение случайной величины x₁(t), то на выходе для случайной величины x₂(t) также будет иметь место нормальное распределение.