ОГЛАВЛЕНИЕ
1.1 Математическое моделирование динамических систем в среде WINDOWS на алгоритмическом языке TURBO-BASIС 3
1.2 Программа fbndiv.bas. Решение дифференциальных уравнений 4
в форме Коши методом Рунге-Кутта (язык TURBO-BASIC) 4
1.3 Моделирование ДС методом понижения порядка производной в среде проблемно ориентированных пакетов прикладных программ. 19
1.4 Программная система МIK 21
1.5 Общие сведения о программном комплексе «МВТУ» 23
1.6 Программная система MATLAB 25
1.6 Расширения ППП MATLAB для идентификации динамических объектов и систем 26
1.7 Расширения ППП MATLAB для исследования электротехнических объектов и систем 28
1.7.1 Основные особенности 29
Введение
Математическое моделирование явлений и процессов, происходящих на технических объектах и в системах управления, является средством исследования их режимов работы, выбора структурных схем и параметров, обеспечивающих оптимальное значение критериев качества машин и механизмов: надежности; динамической загруженности; энергозатрат; быстродействия; перерегулирования; колебательности, среднеквадратических отклонений; линейных и квадратичных интегральных критериев, а также оценок технико-экономической эффективности.
Появление мощных ПЭВМ общего применения типа IBM РС-Pentium, промышленных компьютеров, построенных на базе тех же процессоров, что и в ПЭВМ, резко повысило возможности применения современной теории автоматического управления, предполагающей использование эталонных, прогнозирующих, восстанавливающих математических моделей технических объектов и методов имитационного моделирования для реализации алгоритмов оптимального управления, требующих быстрого выполнения больших объемов вычислительных операций.
Во второй части пособия даются понятия и алгоритмы идентификации моделей статических и динамических режимов работы технических объектов и систем, приводятся методы получения и формы представления математических моделей динамических систем, описываются принципы и методы моделирования технических объектов и систем на аналоговых машинах, алгоритмы и программные средства для решения задач моделирования и идентификации на ПЭВМ.
Анализ принципов построения адаптивных систем автоматического управления техническими объектами с контурами моделирования и идентификации позволил предложить структуру и алгоритмы работы адаптивных САУ техническими объектами с идентификацией моделей по результатам мониторинга средствами SCADA-систем.
Включение в учебный план специальностей 050702 "Автоматизация и управление" дисциплины "Моделирование и идентификация", а специальности 050718 — "Электроэнергетика" — дисциплины "Математические задачи и компьютерное моделирование в энергетике" преследовало цель – подготовить студентов к освоению принципов построения математических моделей объектов и систем управления, а также методов и средств их имитационного моделирования.
Алгоритмы и программные средства для решения задач моделирования и идентификации динамических систем на пэвм
Программные средства — это операционные системы, языки программирования, стандартные и оригинальные программы для решения задач синтеза и анализа ДС, а также специальные, так называемые проблемно ориентированные, пакеты прикладных программ (ППП).
Математическое моделирование динамических систем в среде windows на алгоритмическом языке turbo-basiс
Для анализа эффективности применения различных программных средств при решении задач исследования ДС сформулируем контрольную задачу на примере простой ДС, описываемой дифференциальным уравнением второго порядка:
(1.1)
где A0=1, A1=2, A2=4, B0=1,
U1(t) = AOU∙(1 - е-t/Tu), AOU = 1, Tu = 10.0.
Преобразуя (1.1) в форму Коши, получим
(1.2)
или в матрично-векторной форме
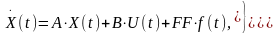(1.3)
где X(t)={X1(t),X2(t)},U(t)=U1(t),f(t)=0,
X0(t)={0,0}.
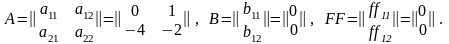
a11 = 0, a12 = 1, a21 = -A2/Ao, a22 = -A1/Ao, = -2,
a22 = -A1/Ao = -2,
b11 = 0, b12 = Bo/Ao, ff11 = 0, ff12 = 0.
Уравнения (1.2), (1.3) пригодны для решения численными методами. Для оценки адекватности численных решений уравнений (1.3) получим аналитическое решение (1.1) операционным методом. Характеристическое уравнение, соответствующее уравнению (1.1)
D(p) = Ao∙p2 + A1∙p + A2 = 0, (1.4)
имеет корни
(1.5)
Из (1.5) следует, что ДС, описываемая уравнением (1.1), устойчива.
Выполнив необходимые (в соответствии с операционным методом решения дифференциальных уравнений) действия, получим следующее эталонное решение:
Y(t) = 0.0080649 ∙ е-10t + 0.28927 ∙ е-1.694t ∙ sin (1.73t - 1.694) +
+ 0.25044 + 0.05191 ∙ е-2.9911t ∙ sin (1.73t - 2.9911). (1.6)
Программа fbndiv.Bas. Решение дифференциальных уравнений в форме Коши методом Рунге-Кутта (язык turbo-basic)
Рассмотрим программу на языке BASIС, реализующую алгоритм метода Рунге-Кутта для решения уравнений типа (1.3). Будем придерживаться следующей методики изложения: приводится фрагмент программы и описывается его алгоритм, анализируются особенности операторов, используемых в данном фрагменте, и предлагаются варианты альтернативных решений программы.
10 'Программа — решение системы диф. уравнений в форме Коши
20 'dY(t)/dt = A∙Y(t)+B∙U(t)+FF∙f(t),
30 'Z(t) = C∙Y(t),
40 'Y(t) – вектор координат пространства состояний размером N,
50 'U(t) – вектор управляющих воздействий размером М,
60 'f(t) – вектор возмущающих воздействий Nf,
70 'A – числовая матрица размером N x N,
80 'B – числовая матрица размером N x M,
90 'FF – числовая матрица размером N x Nf,
100 'Z(t) – вектор выходных координат динамической системы размером Nz,
110 'C – числовая матрица размером Nz x N,
120 'Yo – вектор начальных условий размером N,
130 'TZERO – начальное время интегрирования,
140 'TFIN – конечное время интегрирования,
150 'DT – шаг интегрирования,
160 'NPT – число расчетных интервалов в диапазоне [TZERO, TFIN].
Операторы 10, 20, 30,..., 160 выполняют одну функцию – описание в тексте программы исходных данных решаемой задачи. Форма представления операторов описания (их еще называют "комментарии"):
<NN> <'> < любой текст> (1.7)
Альтернативную задачу выполняет оператор REM. Его форма представления:
<NN> <REM> < любой текст> (1.8)
ПРИМЕР:
10 REM Программа – решение системы диф. уравнений в форме Коши
20 REM dY(t)/dt = A∙Y(t) + B∙U(t) + FF∙f(t),
30 REM Z(t) = C∙Y(t),
40 REM Y(t) – вектор координат пространства состояний размером N,
Внимательно изучите постановку задачи и исходные данные по операторам 10, 20, ..., 160 и материалам, приведенным выше.
200 CLS
210 ST$= TIME$
КОММЕНТАРИИ. Оператор CLS осуществляет очистку экрана.
Информация, находящаяся на экране, стирается, курсор размещается в левом верхнем углу экрана.
Оператор TIME$ (time – время) позволяет контролировать время решения задачи. В программе fbndiv переменной ST$ присваивается значение TIME$, равное времени начала выполнения программы. В 940-м операторе основной программы переменной ET$ присваивается значение TIME$, равное времени окончания выполнения программы: 940 ET$=TIME$.
Символ $ (доллар) используется для явного задания строкового типа переменной. Символ записывается последним в имени переменной. Варианты: % – переменная целого типа, ! – переменная с обычной точностью, # – переменная с двойной точностью.
215 INPUT" ВЫДАЧА НА ЭКРАН-1, НА ЭКРАН И ПРИНТЕР-2"; LPRT
220 'СЧИТЫВАНИЕ ДАННЫХ
230 INPUT"ВВЕДИТЕ РАЗМЕРНОСТЬ ВЕКТОРОВ И МАТРИЦ N, M, Nf, Nz"; N, M, Nf, Nz.
КОММЕНТАРИИ. С помощью оператора INPUT выполняется ввод с клавиатуры данных любого типа и присвоение их значений переменным, объявленным в программе. Форма представления оператора INPUT:
<NNN>INPUT<"подсказка">;<переменная>,<переменная>
240 '*** резервирование памяти ***
250 DIM Z(NZ), U(M), PRA(N), A(N,N), B(N,M), C(NZ,N), XFN(N), FF(N,Nf), f(Nf), y(n)
260 DIM SAVEY(N), PHI(N), A1(N), A2(N), A3(N), AOU(M), AOF(Nf), TU(M), TF(Nf), Y0(n)
КОММЕНТАРИИ. Операторы типа
250 DIM Z(NZ), U(M), PRA(N), A(N,N), B(N,M), ... используются для резервирования оперативной памяти под массивы переменных. Оператор DIM (сокращенная мнемоника оператора DIMension – измерение, размерность) используется для явного объявления (задания) массива. Форма представления оператора DIM:
<NNN> DIM имя-массива (размерность) [имя-массива (размерность)]
Имя массива – это любое имя, присваиваемое массиву. Размерность – это целая переменная, числовое выражение или положительное число, целая часть которого определяет максимальное значение соответствующего выражения.
В BASIС могут использоваться одномерные и многомерные массивы до 255 измерений.
Отдельный элемент массива обозначается именем массива и списком индексов. Список индексов должен содержать столько индексов, сколько измерений имеет соответствующий массив.
Элементы одномерного массива располагаются один за другим в последовательно расположенных байтах памяти. Двумерный массив располагается построчно. Элементы многомерных массивов расположены так, что вначале изменяется самый правый индекс.
270 DEFSNG Y, Z, U
КОММЕНТАРИИ. Оператор DEF... (DEFine – определить) объявляет тип переменной. В программе оператор DEFSNG объявляет, что переменные Y, Z, U – это переменные с обычной точностью.
Возможные варианты:
DEFINT – целые переменные,
DEFDBL – переменные с двойной точностью,
DEFSTR – строковые переменные.
280 *построчно вводятся элементы матриц* 285 PRINT "Введите члены матрицы А" 290 FOR I=1 to N 300 FOR J=1 to 310 PRINT "A("I","J")";:INPUT A(I,J) 320 NEXT J 330 NEXT I |
А – это числовая матрица при векторе координат пространства состояний X(t) модели ДС (1.3) |
КОММЕНТАРИИ. Оператор PRINT (print – напечатать) осуществляет вывод данных на экран дисплея. В операторе 280 — это текстовая информация, находящаяся между кавычками:
ВВЕДИТЕ ЧЛЕНЫ МАТРИЦЫ А,
а в операторе:
310 PRINT "A("I","J")";: INPUT A(I,J),
это имя I-го, J-го элемента матрицы A – A(I,J).
Далее оператор:
INPUT A(I,J)
предлагает пользователю ввести с клавиатуры значение I-го, J-го элемента матрицы A. Например, для A (1,1) это будет выглядеть так: A(1,1) =?
Пользователь должен набрать на экране значение I-го, J-го элемента матрицы A (I,J) и нажать клавишу ENTER. Например, A (1,1)=0.0, тогда на вопрос:
А(1, 1) = ?, пользователь отвечает:
0.0→ ENTER
С помощью операторов
290 FOR I=1 to N 300 FOR J=1 to N .................... 320 NEXT J 330 NEXT I |
Элементы матриц вводятся построчно. Например, элементы матрицы – A из модели (1.3) при N = 2, вводятся в следующей последовательности: A(1.1), A(1,2), A(2,1), A(2,2). |
организуются циклы для ввода элементов матрицы A.
335 Print "Введите члены матрицы B" 340 FOR I=1 to N 350 FOR J=1 to M 360 Print B("I","J")";:Input B(I,J) 370 NEXT J 380 NEXT I
|
В — это числовая матрица при векторе управляющих воздействий X(t) в модели ДС(1.3). |
385 Print" Введите члены матрицы C" 390 For I=1 To Nz 400 For J=1 To N 405 Print "C("I","J")";:Input C(I,J) 420 Next J 430 Next I |
C – это числовая матрица при векторе наблюдаемых координат для модели (1.3): Z(T)=C∙X(T) |
440 '*** Вводится вектор начальных условий Yo *** 445 PRINT" введите вектор начальных условий Y0" 450 FOR I=1 to N 460 PRINT"Y0("I")";:INPUT Y0(I) 470 NEXT I
|
В модели (1.3) вектор начальных условий обозначен X0(t). |
480 '*** вводятся параметры вектора U(t) *** 490 '*** Ui(t) =AOUi ∙ [1.0 - EXP(-TU1i ∙ XT)] 500 'AOUi - амплитуда i-го воздействия 510 'TU1 - постоянная времени воздействия, TU1i= 1/TUi1 520 '- XT - независимый аргумент - время 525 '***Вводится амплитуда Ui * 527 Print "Введите амплитуду Ui" 530 FOR I=1 to M 540 PRINT "Ui("I")";:INPUT aou(i) 550 NEXT I 555 '*** вводится постоянная времени для Ui, TU=1/TUi1 *** 557 PRINT "Введите постоянную времени TU" I 560 FOR I=1 to M 570 PRINT"TU("I")";:INPUT TU(i) 580 NEXT |
В рассматриваемом примере — в качестве управляющего воздействия принята возрастающая экспонента (см. оператор 490). В общем случае пользователь должен эту часть программы формировать исходя из условий работы своего динамического объекта (или ДС). |
590'***вводятся параметры вектора f(t) *** 600 '*** fi(t) = AOFi ∙ [1 - exp(- TFINi ∙ XT)] *** 605 '*** вводится амплитуда fi(t) *** 607 print "введите амплитуду fi(t)" 610 for i=1 to nf 620 print "AOF("i")";:input AOF (i) 630 next i 633 '*** постоянная времени воздействия fi(t), TFi=1/ TFi *** 635 print "введите постоянную времени TFi " 640 for i=1 to nf 650 print " TF ("i")";:input TF(i) 660 next i |
В рассматриваемом примере в качестве возмущающего воздействия принята возрастающая экспонента (см. оператор 600). В общем случае пользователь должен эту часть программы формировать исходя из условий работы динамического объекта (или ДС). |
661 '*** вводится матрица FF *** 662 PRINT "Введите матрицу FF" 665 FOR I=1 to N 666 FOR J=1 to Nf 667 Print "FF("I","J")";:Input FF(i,j) 668 NEXT J 669 NEXT I |
FF — это числовая матрица при векторе возмущающих воздействий f(t) в модели ДС (1.3). |
670 '*** вводятся временные интервалы ***
674 PRINT "Введите временные интервалы TZERO, TFIN, DT";:INPUT TZERO, TFIN, DT
Оператором 674 вводятся параметры численного алгоритма:
TZERO – начальное время интегрирования,
TFIN – конечное время интегрирования,
DT – шаг интегрирования,
NPT – число расчетных интервалов в диапазоне [TZERO, TFIN].
Для ДС с математической моделью высокого порядка (N>2) более удобным способом ввода информации является ввод данных из файла данных, который в BASIС оформляется в виде подпрограммы, например:
8000'****************Данные ****************
8010 'размерность векторов и матриц
8020 DATA 2,1,1,2
8030 'элементы матрицы A
8040 DATA 0.0,1.0
8050 DATA -4.0,-2.0
8060 'матрица В
8070 DATA 0.0
8080 DATA 1.0
8090 'матрица С
8100 DATA 1.0,1.0
8110 DATA 1.0,1.0
8120 'вектор Yo
8130 DATA 0.0,0.0
8135 'параметры U(t): AOU,TU
8140 DATA 1.0
8150 DATA 0.05
8155 'параметры f(t): AOF,TF
8160 DATA 0.0
8165 DATA 0.0
8170 'матрица FF
8175 DATA 0.0
8180 DATA 0.0
8185 'временные интервалы
8190 DATA 0.0,0.5,0.02
Рассмотрим вариант программы с вводом исходных данных из подпрограммы 8000.
Оператор, позволяющий вводить данные с клавиатуры
230 Input "Введите размерность векторов и матриц N, M, Nf, Nz"; N, M, Nf, Nz,
должен быть заменен на оператор Read (читать, считывать), который присваивает переменным значения, заданные оператором Data в файле исходных данных (в подпрограмме 8000). Стандартная форма представления оператора Read:
<NNN> Read переменная, [переменная] ....
В программе с вводом данных из подпрограммы 8000:
230 Read N, M, Nf, Nz 'Pазмерность векторов и матриц
В подпрограмме 8000 оператору 230 будет соответствовать оператор Data:
8020 Data 2, 1, 1, 2
Приведем варианты ввода элементов матриц с клавиатуры и из подпрограммы 8000:
с клавиатуры: 285Print" Введите члены матрицы А" 300 For J=1 to N 310Print "A("I","J")";:Input A(I,J) 320 Next J 330 Next I |
из подпрограммы 8000: 290 For I=1 to N 300 For J=1 to N 310 Read A(I,J) 'Вводится матрица А 320 Next J 330 Next I |
В подпрограмме 8000 операторам 290 – 330 будут соответствовать операторы
Data:
8030 'элементы матрицы A
8040 Data 0.0,1.0
8050 Data -4.0,-2.0
Аналогично вводятся элементы матриц B, C, FF. Приведем без комментариев фрагменты вариантов ввода данных с клавиатуры и из подпрограммы 8000.
Ввод вектора начальных условий Yo:
с клавиатуры: 450 For I=1 to N 460 Print"Y0("I")";: Input Y0(I) 470 Next I
|
из подпрограммы 8000: 450 For I=1 to N 460 Read Y0(I) 'вектор начальных условий Yo 470 Next I В подпрограмме 8000 операторам 450-470 будут соответствовать операторы DATA: 8120 'вектор Yo 8130 DATA 0.0,0.0 |
Ввод параметров вектора U(t),
с клавиатуры: 527Print"Введите амплитуду Ui" 530 FOR I=1 to M 540 Print "Ui("I")";: Input aou(i) 550 Next I 560 For I=1 to M 570 Print"TU("I")";:Input TU(i) 580 Next I
|
из подпрограммы 8000: 530 For I=1 to M 540 Read AOU(I) 'вводится амплитуда Ui 550 Next I 560 For I=1 to M 570 Read TU(I) 'вводится TU=1/Tui1 580 Next I В подпрограмме 8000 операторам 530-580 будут соответствовать операторы Data: 8135 'параметры U(t): AOU,TU 8140 Data 1.0 8150 Data 0.05
|
Ввод параметров численного алгоритма и временных интервалов, с клавиатуры:
674 PRINT "Введите временные интервалы TZERO, TFIN, DT";:INPUT TZERO, TFIN, DT
из подпрограммы 8000:
670 Read TZERO, TF, DT '*** вводятся временные интервалы ***
Оператору 670 в подпрограмме 8000 соответствуют операторы Data:
8185 'временные интервалы
8190 Data 0.0,0.5,0.02
680'*********Основная программа ***********
685 For I=1 to N
690 XFN(I) = 0.0
700 Next I
702 For I=1 to N
704 Y(I) = Y0(I)
706 Next I
710 NPT1 = (TFIN - TZERO)/DT
720'***NPT – число расчетных интервалов на диапазоне [TZERO,TFIN]***
730 NPT = INT(NPT1)
Операторы 685-700 подготавливают (обнуляют) элементы вектора XFN. Вектор XFN выполняет вспомогательные функции в подпрограмме 2000.
Операторы 702-706 устанавливают начальные условия для элементов вектора Y(t).
Операторы 710, 730 используются для вычисления числа расчетных интервалов на оси времени t.
Функция INT осуществляет вычисление наибольшего целого от вещественного числа NPT1.
735 GOSUB 1000 '*** вызывается подпрограмма печати исходных данных *** 740 XT = 0.0 742 H=DT 744 IYY=1 750 '** открывается цикл расчета ординат ДС ** |
XT – текущее время интегрирования, Н – шаг интегрирования, IYY – номер расчетного интервала. |
770 '** вызываются подпрограммы 2000,3000,4000,5000,6000,7000 **
780 For IX = 1 to NPT
790 IXX = 0
800 Gosub 2000 '** подпрограмма расчета диф. ур. методом Рунге-Кутта ***
810 Gosub 3000 '** подпрограмма расчета Ui(t) **
820 Gosub 4000 '*** подпрограмма расчета fi(t) ***
830 Gosub 5000 '** подпрограмма расчета правой части диф.уравнений **
840 If L = 2 Then 860
850 Goto 800
860 Gosub 6000 '** подпрограмма расчета вектора Z(t) **
870 Gosub 7000 '** вызывается подпрограмма выдачи результатов **
890 IYY = IYY + 1
900 Next IX
Операторы 780-900 составляют основной расчетный цикл, в котором реализуется численный алгоритм Рунге-Кутта. Целая переменная IXX в подпрограмме 2000 используется для управления процессом вычислений.
Целая переменная L формируется в подпрограмме 2000 и используется в основной программе для управления процессом вычислений.
910 '* закрывается цикл IX — [780,890], в котором рассчитываются Yi(t) и Zi(t)*
920 PRINT "———————————————-"
925 IF LPRT=1 THEN 940
930 LPRINT"———————————————"
940 ET$=TIME$
950 PRINT "начало работы программы" ST$
970 PRINT "конец работы программы" ET$
971 IF LPRT=1 THEN 990
975 LPRINT "начало работы программы" ST$
980 LPRINT "конец работы программы" ET$
990 '****** это конец программы *******'
995 end
LPRT — переменная-признак, задается в исходных данных (в 215-м операторе программы) и позволяет задать форму выдачи результатов решения задачи.
LPRT=1 ВЫДАЧА НА ЭКРАН,
LPRT=2 НА ЭКРАН И ПРИНТЕР.
1000 '*** 1000 - подпрограмма печати исходных данных *** 1010 Print " Решение диф. уравнений методом Рунге-Кутта " 1020 Print 1030 Print " Данные " 1040 Print 1052 Print "N=" N; M="M; "Nf=" Nf; "Nz="Nz 1060 Print " Матрица А" 1100 Lprint " Данные " 1070 Print 1075 If LPRT=1 Then 1120 1080 Lprint "Решение диф. уравнений методом Рунге-Кутта" 1090 Lprint 1110 Lprint 1111 Lprint "N=" N; "M=" M; "Nf=" Nf; "Nz=" Nz |
Оператор Print (print –напечатать) обеспечивает вывод числовых и строковых данных на экран дисплея. Lprint – обеспечивает вывод числовых и строковых данных на принтер и экран дисплея. |
1112 Lprint " Матрица А" 1115 Lprint 1120 For I=1 to N 1130 For J=1 to N ¦ 1140 Print using "###.#####"; A(I,J); 1141 If LPRT=1 Then 1143 Lprint using "###.#####"; A(I,J); 1150 Next J 1152 Print 1155 Next I 1160Print |
Операторы типа: Print Jusing "###.#####"; A(I,J)> осуществляют вывод данных по шаблону и отличаются от оператора PRINT тем, что позволяют управлять формой представления выводимых данных. Форма представления данного определяется шаблоном и не зависит от его значения. Оператор Print using: <Print using шаблон; выражение [выражение] ... [;]> Шаблон – строковая константа или перемен- ная,определяющая форму вывода значений. Выражение – любое числовое или строковое выражение. Символ ";" в конце оператора отменяет переход на следующую строку после завершения вывода данных. |
Шаблон для числовых значений задает поле вывода фиксированной длины. Длина этого поля определяется количеством символов в шаблоне. Выводимое значение преобразуется к десятичному виду или к представлению в экспоненциальной форме в зависимости от значения шаблона, а затем переносится в поле вывода.
Символы числового шаблона.
# – цифровая позиция поля вывода всегда присутствует в выводимой строке и может содержать цифру, знак числа или пробел. В крайних левых позициях выводятся пробелы, если в выводимом числе меньше цифр, чем определено шаблоном.
. – задается местоположение десятичной точки. Слева располагается целая часть числа, а справа – дробная1.
1180 PRINT " МАТРИЦА В"
1182 PRINT
1183 IF LPRT=1 THEN 1220
1185 LPRINT
1190 LPRINT " МАТРИЦА В"
1210 LPRINT
1220 FOR I=1 to N
1230 FOR J=1 to M
1240 PRINT USING "###.#####"; B(I,J)
1241 IF LPRT=1 THEN 1250
1243 LPRINT USING "###.#####"; B(I,J)
1250 NEXT J
1260 NEXT I
1290 PRINT " МАТРИЦА C"
1295 PRINT
1296 IF LPRT=1 THEN 1340
1300 LPRINT " МАТРИЦА C"
1320 LPRINT
1340 FOR I=1 to Nz
1350 FOR J=1 to N
1360 PRINT USING "###.#####"; C(I,J);
1361 IF LPRT=1 THEN 1370
1363 LPRINT USING "###.#####"; C(I,J);
1370 NEXT J
1375 PRINT
1376 IF LPRT=1 THEN 1380
1378 LPRINT
1380 NEXT I
1390 PRINT " МАТРИЦА FF"
1400 PRINT
1405 IF LPRT=1 THEN 1430
1410 LPRINT " МАТРИЦА FF"
1420 LPRINT
1430 FOR I=1 to N
1440 FOR J=1 to Nf
1450 PRINT USING "###.#####"; FF(I,J)
1452 IF LPRT=1 THEN 1460
1453 LPRINT USING "###.#####"; FF(I,J)
1460 NEXT J
1470 NEXT I
1480 PRINT
1485 PRINT " Вектор начальных условий Yo "
1490 PRINT
1492 IF LPRT=1 THEN 1520
1500 LPRINT
1510 LPRINT " Вектор начальных условий Yo "
1515 LPRINT
1520 FOR J=1 to N
1530 PRINT USING "###.#####"; Y0(J);
1532 IF LPRT=1 THEN 1540
1533 LPRINT USING "###.#####"; Y0(J);
1540 NEXT J
1545 PRINT
1550 PRINT " параметры U(t) "
1560 PRINT
1570 PRINT
1580 PRINT " параметры f(t) "
1582 IF LPRT=1 THEN 1598
1589 LPRINT
1590 LPRINT " параметры U(t) "
1592 LPRINT
1594 LPRINT
1596 LPRINT " параметры f(t) "
1598 FOR J=1 to M
1600 PRINT " J= "; J; "AOU="; AOU(J); "TU="; TU1(J)
1610 NEXT J
1660 FOR J=1 to Nf
1670 PRINT " J= "; J; "AOF("J")="; AOF(J); "TF("J")="; TF(J)
1680 NEXT J
1690 PRINT
1700 PRINT " параметры численного алгоритма "
1705 PRINT "TZERO – начальное время интегрирования ="; TZERO: PRINT
1710 PRINT "TFIN – конечное время интегрирования="; TFIN:PRINT
1715 PRINT "DT – шаг интегрирования="; DT:PRINT
1717 PRINT "NPT – число расчетных интервалов в диапазоне [TZERO, TFIN]"; NPT
1720 PRINT
1725 PRINT""
1730 PRINT"I——— I———I———I ———I———I———I———I———I"
1735 PRINT "I NI XT I Y1(t) I Y2(t) I Z1(t) I Z2(t) I U1(t) I f1(t) I"
1740 PRINT I——— I———I———I ———I———I———I———I———I"
1750 IF LPRT=1 THEN 1920
1755 LPRINT
1760 LPRINT " параметры численного алгоритма "
1770 LPRINT "TZERO – начальное время интегрирования"; TZERO: LPRINT
1780 LPRINT "TFIN – конечное время интегрирования"; TFIN:LPRINT
1790 LPRINT "DT – шаг интегрирования"; DT:LPRINT
1800 LPRINT "NPT – число расчетных интервалов в диапазоне [TZERO, TFIN]"; NPT
1810 LPRINT
1870 LPRINT "
1880 LPRINT "I———I———I———I———I———I———I———I———I"
1890 LPRINT"'I N I XT I Y1(t) I Y2(t) I Z1(t) I Z2(t) I U1(t) I f1(t) I"
1900 LPRINT"I———I———I———I———I———I———I———I———I"
1920 RETURN
Далее представлены подпрограммы, которые выполняют обработку информации в соответствии с алгоритмом численного интегрирования Рунге-Кутта 4-го порядка для системы дифференциальных уравнений в форме Коши (3.1).
2000 '*** 2000 - подпрограмма расчета диф. уравнений *** 2010 IXX = IXX + 1 2020 '************************** 2030 ON IXX GOTO 2040, 2070, 2160, 2230, 2310 2040 L = 1 2050 '************************** 2060 RETURN 2070 FOR J2 = 1 to N 2080 SAVEY (J2) = Y(J2) 2090 PHI (J2) = XFN (J2) 2100 Y(J2) = SAVEY(J2) + 0.5 * H * XFN(J2) 2110 NEXT J2 2120 '************************** На каждом шаге интегрирования производится четыре обращения к подпрограмме 2000 из головной программы. На втором и четвертом обращениях переменная ХТ увеличивается на 0.5•Н (операторы 2130 и 2270). |
Целая переменная IXX управляет пошаговым процессом численного интегрирования на интервале фиксированного шага H. Оператор 2030 ON IXX GOTO 2040,... передает процесс вычислений, соответственно, при: IXX=1 по метке 2040, IXX=2 по метке 2070, IXX=3 по метке 2160, IXX=4 по метке 2230, IXX=5 по метке 2310. |
Перед первым обращением к подпрограмме 2000 содержимое переменной IXX должно быть обнулено (см. оператор 790); затем после каждого полного шага интегрирования IXX автоматически устанавливается в нуль (с помощью операторов 2350 в подпрограмме 2000).
В подпрограмме 2000 используются следующие обозначения переменных:
N – порядок системы дифференциальных уравнений;
XFN – массив для значений производных dY/dt из-подпрограммы 5000 – расчет правой части дифференциального уравнения;
SAVEY – массив промежуточных значений Y(t) на интервале, равном шагу интегрирования H;
PHI – массив промежуточных значений XFN(t) на интервале, равном шагу интегрирования H;
Y – массив для значений переменных вектора состояния;
H – шаг интегрирования;
XT – текущее время интегрирования;
L=1 – указывает, что процесс интегрирования не завершен;
L=2 – указывает, что выполнен очередной шаг интегрирования;
IXX – количество обращений к подпрограмме 2000 на данном шаге ин- тегрирования.
2130 XT = XT + 0.5 * H 2140 L = 1 2150 RETURN 2160 FOR J3 = 1 to N 2170 PHI(J3) = PHI(J3) + 2.0 * XFN(J3) 2180 Y(J3) = SAVEY(J3) + 0.5 * H * XFN(J3) 2190 NEXT J3 2200 L = 1 2210 '************************** 2220 RETURN 2230 FOR J4 = 1 to N 2240 PHI(J4) = PHI(J4) + 2.0 * XFN(J4) 2250 Y(J4) = SAVEY(J4) + H * XFN(J4) 2260 NEXT J4 2270 XT = XT + 0.5 * H 2290 L = 1 2300 RETURN |
В циклах: 2070 - 2110 по J2, 2070 - 2110 по J3, 2070 - 2110 по J4, 2070 - 2110 по J5 осуществляются вычисления по алгоритму Рунге-Кутта четвертого порядка, который описан выше. |
2310 FOR J5 = 1 to N
2320 Y(J5) = SAVEY(J5) + (H/6.0) * (PHI(J5) + XFN(J5))
2330 NEXT J5
2340 L = 2
2350 IXX = 0
2360 '**************************
2370 RETURN
3000 '*** 3000 подпрограмма расчета Ui(t) ***
3010 FOR IIM = 1 to M
3020 U(IIM) = AOU(IIM) * (1.0 - 1.0/EXP(XT * TU(IIM)))
3040 NEXT IIM
3050 RETURN
Подпрограмма расчета Ui(t) составляется пользователем для конкретных условий эксплуатации ДС.
4000 '*** 4000 - подпрограмма расчета fi(t) - ***
4010 FOR I = 1 to Nf
4020 F(I) = AOF(I) * (1.0 - 1.0/EXP(XT * TF(I)))
4030 NEXT I
4040 RETURN
Подпрограмма расчета fi(t) составляется пользователем для конкретных условий эксплуатации ДС.
5000 '*** 5000 — ПОДПРОГРАММА РАСЧЕТА ПРАВОЙ ЧАСТИ ДИФ.УРАВНЕНИЯ ***
5005 FOR I = 1 to N 5010 A1 (I) = 0.0 5020 FOR J = 1 to N 5030 A1(I) = A1(I) + A(I,J) * Y(J) 5040 NEXT J 5050 NEXT I 5051'************************** 5052 FOR I = 1 to N 5055 A2(I) = 0.0 5060 FOR J = 1 to M 5070 A2(I) = A2(I) + B(I,J) * U(J) 5080 NEXT J 5090 NEXT I 5100 FOR I = 1 to N 5110 A3(I) = 0.0 5120 FOR J = 1 to Nf 5130 A3(I) = A3(I) + FF(I,J) * F(J) 5160 NEXT J 5170 NEXT I |
Подпрограмма составлена для уравнений (10.1). В общем случае подпрограмма расчета правых частей ДС составляется пользователем для конкретных условий эксплуатации ДС.
|
5180 FOR I =1 to N
5190 PRA (I) = A1(I) + A2(I) + A3(I)
5200 NEXT I
5210 '**************************
5220 FOR I = 1 to N
5230 XFN(I) = PRA(I)
5240 NEXT I
5250 RETURN
6000 '*** 6000 - подпрограмма расчета вектора Z(t) ***
6005 FOR IL = 1 to Nz
6010 Z(IL) = 0.0
6020 FOR J = 1 to N
6030 Z(IL) = Z(IL) + C(IL,J) * Y(J)
6040 NEXT J
6050 NEXT IL
6060 RETURN
7000 '*** 7000 - подпрограмма [Результаты] ***
7010 PRINT USING "####";IYY;
7011 PRINT USING " ##.####";XT;
7012 PRINT USING "####.#####";Y(1);
7013 PRINT USING "####.#####";Y(2);
7014 PRINT USING "####.#####";Z(1);
7015 PRINT USING "####.#####";Z(2);
7016 PRINT USING "####.#####";U(1);
7017 PRINT USING "####.#####";f(1)
7019 IF LPRT=1 THEN 7030
7020 LPRINT USING "####";IYY;
7021 LPRINT USING " ##.####";XT;
7022 LPRINT USING "####.#####";Y(1);
7023 LPRINT USING "####.#####";Y(2);
7024 LPRINT USING "####.#####";Z(1);
7025 LPRINT USING "####.#####";Z(2);
7026 LPRINT USING "####.#####";U(1);
7027 LPRINT USING "####.#####";f(1)
7030 RETURN
Качество работы программы fbndiv.bas предлагается проверить путем сравнения численного решения для уравнения (1.1) с эталонным решением (1.6).