6.1.2 Профиль интервала
Для организации связи топологией «точка-точка» проектом предусмотрено построение профиля для проектируемого пролета на данном участке.
Продольный профиль интервала Ижевск-Чистопрудный представлен на рисунке 6.1
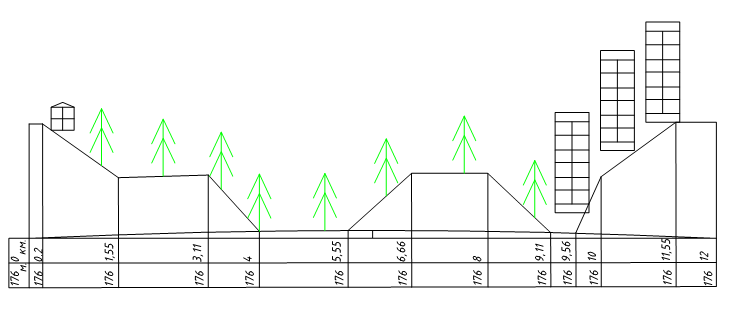
Рисунок 6.1 - Профиль интервала Ижевск-Чистопрудный
6.1.3 Определение длины пролета
Длина пролета определяется по результатам анализа радиорелейной трассы путем измерения расстояния между двумя точками на карте.
Параметры пролетов радиорелейной линии приведены в таблице 6.1:
Таблица 6.1 - Параметры пролетов радиорелейной линии
Параметр |
Ижевск-Чистопрудный |
Длина интервала R0 , м |
12000 |
Расстояние до препятствия R1 , м |
300 |
Ширина препятствия r, м |
80 |
6.1.4Определение величины просвета
Величина просвета, при которой напряженность поля на интервале равна напряженности поля в свободном пространстве, определяется по формуле 6.2:
,
(6.2)
где λ – длина волны;
R0 – длина интервала;
k – относительная координата наиболее высокой точки на профиле определяется по формуле 6.3:
(6.3)
где R1 – расстояние до наиболее высокой точки препятствия;
Длина волны определяется по формуле 6.4:
(6.4)
где с = 3 · 108 м/с – скорость распространения электромагнитной волны в вакууме (для воздуха берется то же значение).
f = 5,4 · 109 Гц – частота СВЧ сигнала.
Расчет длины волны определяется по формуле 6.4:
Расчет пролета:
Расчет относительной координаты наиболее высокой точки на профиле (формула 6.3):
Расчет величины просвета, при которой напряженность поля на интервале равна напряженности поля в свободном пространстве (формула 6.2):
6.1.5 Определение приращения просвета за счет рефракции
Основная сложность расчетов РРЛ определяется тем, что траектория распространения электромагнитной волны непрямолинейна, случайна и зависит от атмосферы и от величины градиента диэлектрической проницаемости атмосферы (gэф). Это явление называется атмосферной рефракцией.
На пересеченном пролете просвет, существующий в течение 80% времени, должен быть равен радиусу минимальной зоны Френеля.
Приращение просвета при средней рефракции выводится по формулам 6.5 и 6.6 и определяется по формуле 6.7:
,
(6.5)
,
(6.6)
(6.7)
где gэф = –10 · 10-8 (м-1) – среднее значение вертикального градиента
диэлектрической проницаемости воздуха;
σ = 8 · 10-8 (м-1) – среднеквадратичное отклонение вертикального градиента диэлектрической проницаемости воздуха.
Значение просвета при отсутствии рефракции находится по формуле 6.8:
(6.8)
Среднее значение просвета на пролете с учетом нормальной атмосферной рефракции определяется из выражений 6.9 и 6.10:
(6.9)
Приращение просвета при средней рефракции находится по формуле 6.10:
(6.10)
Величина относительного просвета при средней рефракции определяется по формуле (6.11):
(6.11)
Расчет приращения просвета при средней рефракции (формула 6.7):
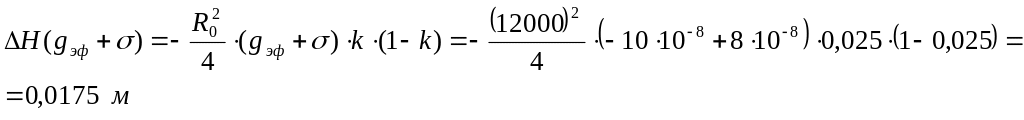
Расчет значения просвета при отсутствии рефракции (формула 6.8):
Расчет приращения просвета с учетом нормальной атмосферной рефракции (формула 6.10):
Расчет среднего значения просвета на пролете с учетом нормальной атмосферной рефракции (формула 6.9):
Расчет величины относительного просвета при средней рефракции (формула 6.11):
Таким образом, просветы с учетом нормальной атмосферной рефракции увеличиваются, что благоприятно скажется на прохождении радиосигнала и на выбор высоты подвеса антенн.