§13. Теорема Штейнера о параллельном переносе о сей.

Рассмотрим сечение произвольной формы площадью F, через его центр тяжести проведем декартовую системы координат.

x₁ = x + b

y₁ = y + b

По чертежу видно, что статические моменты сечения равны нулю

S_x = S_y = 0, тогда осевые моменты инерции относительно новых x₁ и y₁ осей будут обозначаться:

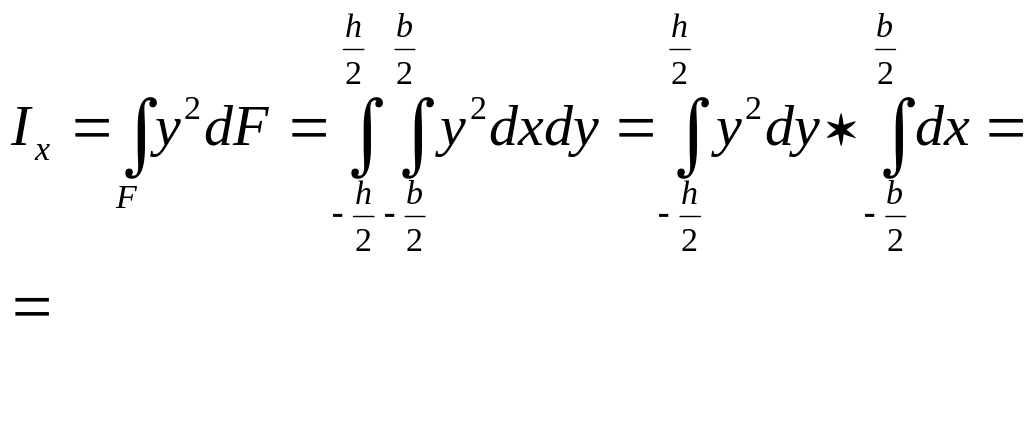
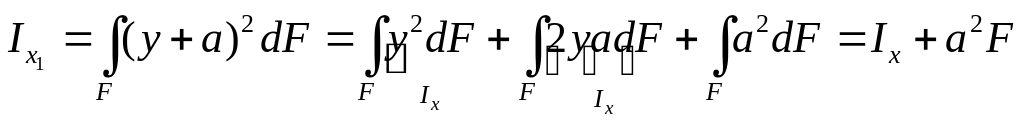
§14. Моменты инерции простых сечений.

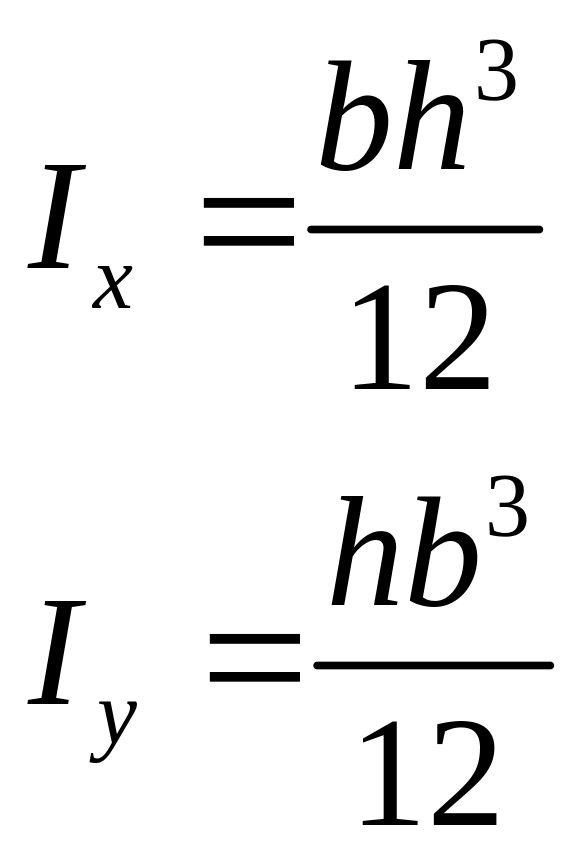
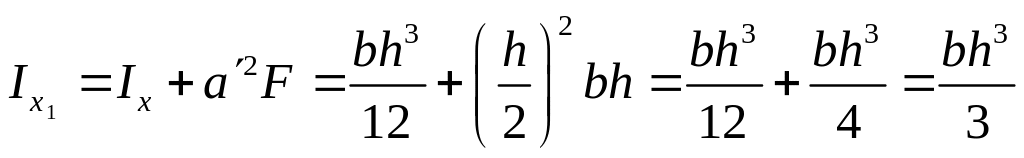
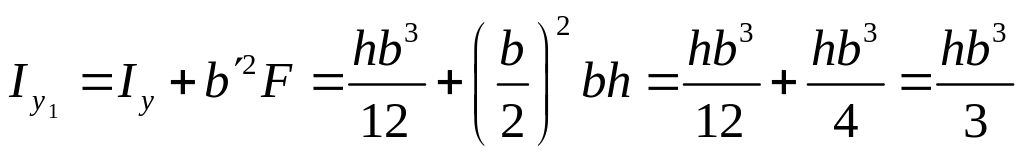
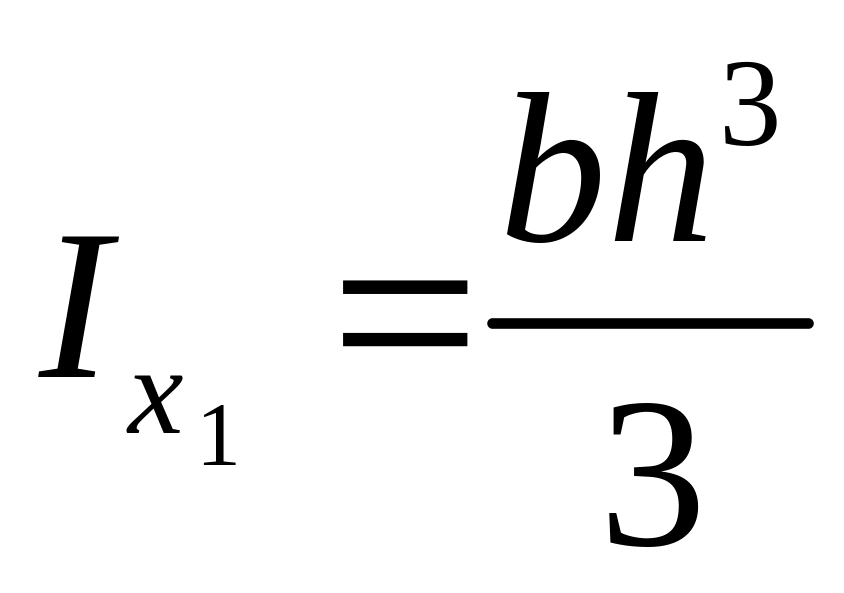
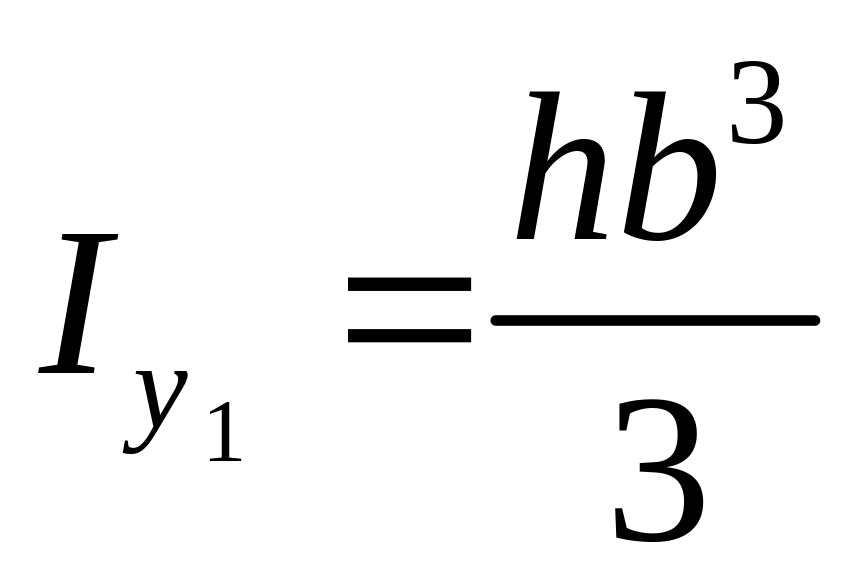
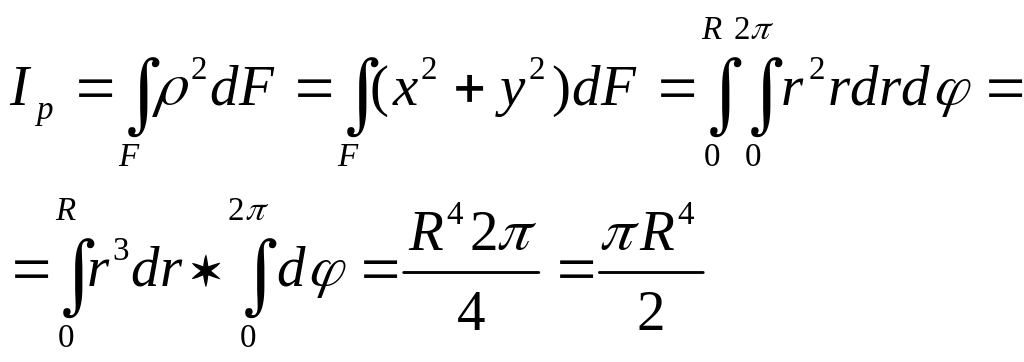
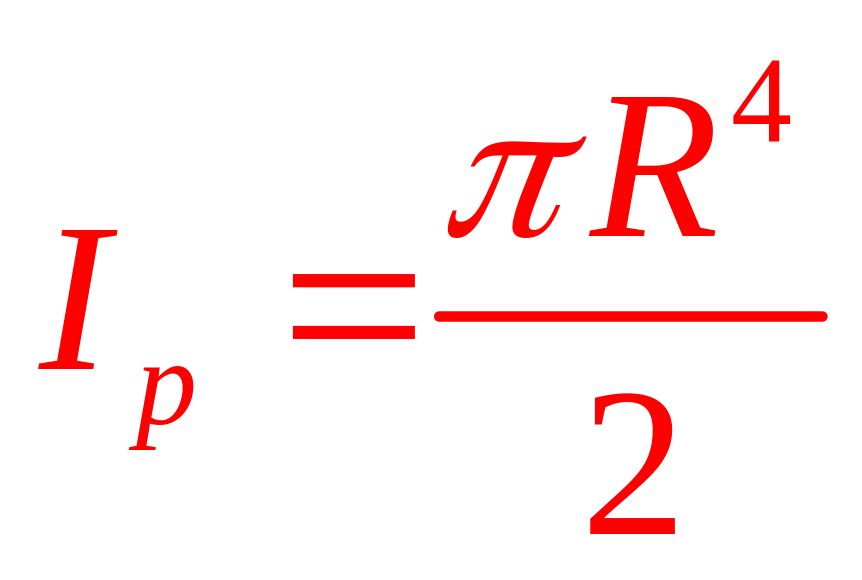
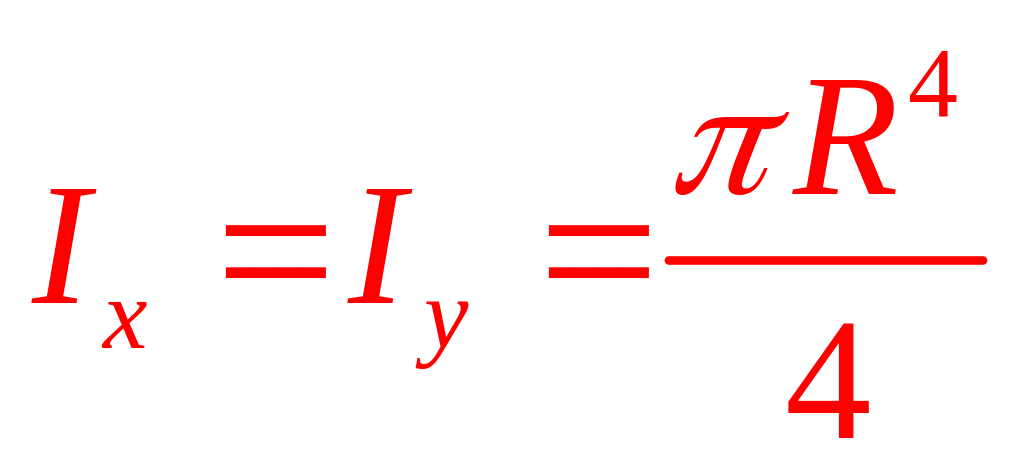
Центр тяжести совпадает с центром координат

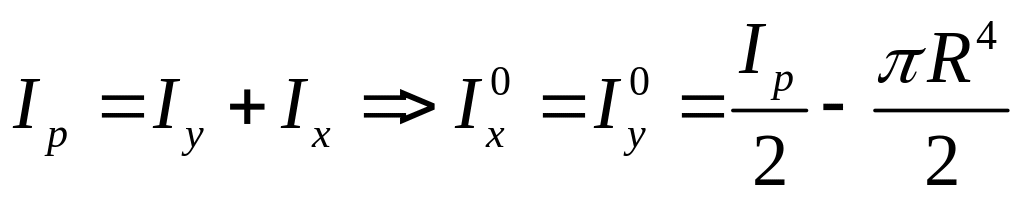
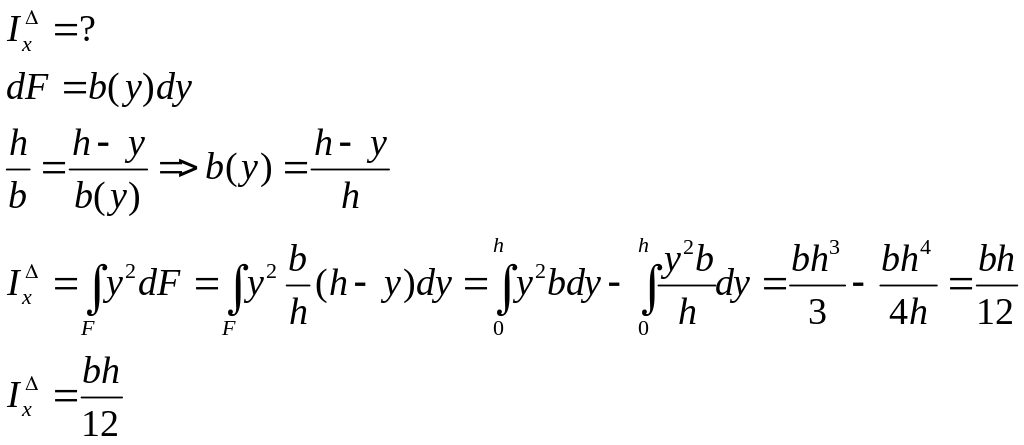
§15. Изменение моментов инерции при повороте осей.

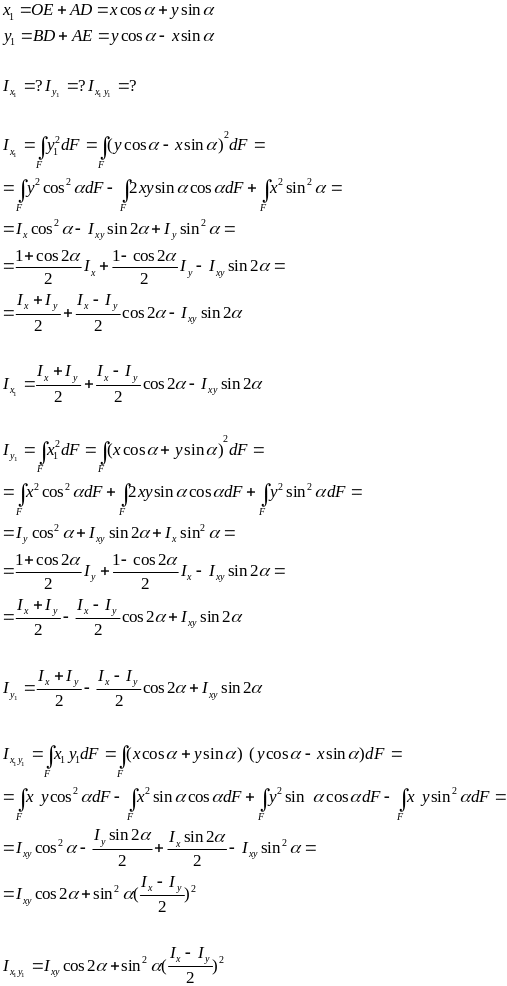
§16. Главные моменты инерции, главные оси инерции.

Наиболее практический интерес представляет собой главные центральные оси относительно которых центральный момент инерции равен 0.

Если оси U, V являются главными центральными осями, то центробежный момент инерции должен быть равен 0.

Получаемые отсюда два значения, α отличаются на 90 и определяют положения главных центральных осей.

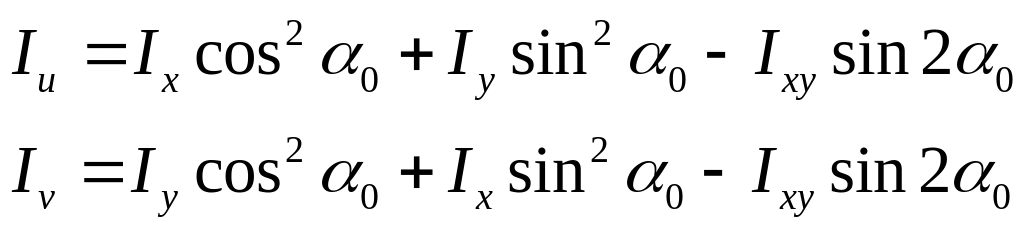
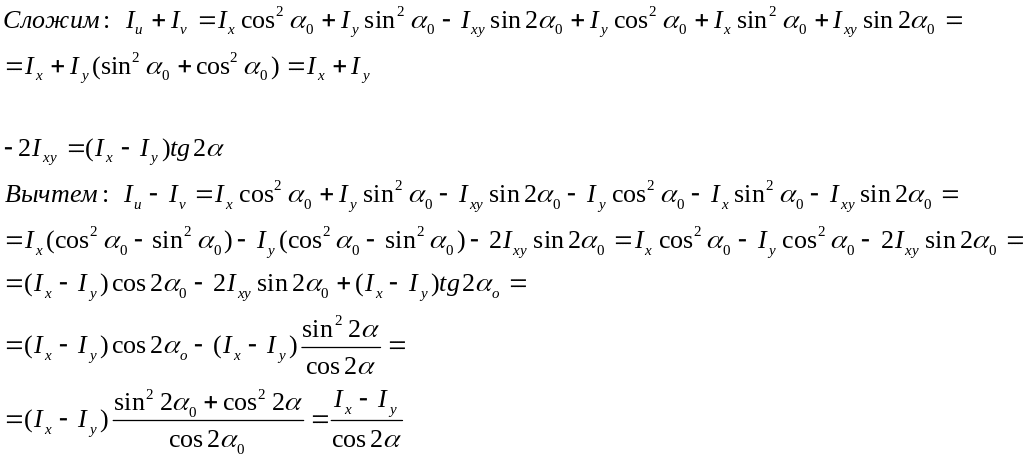
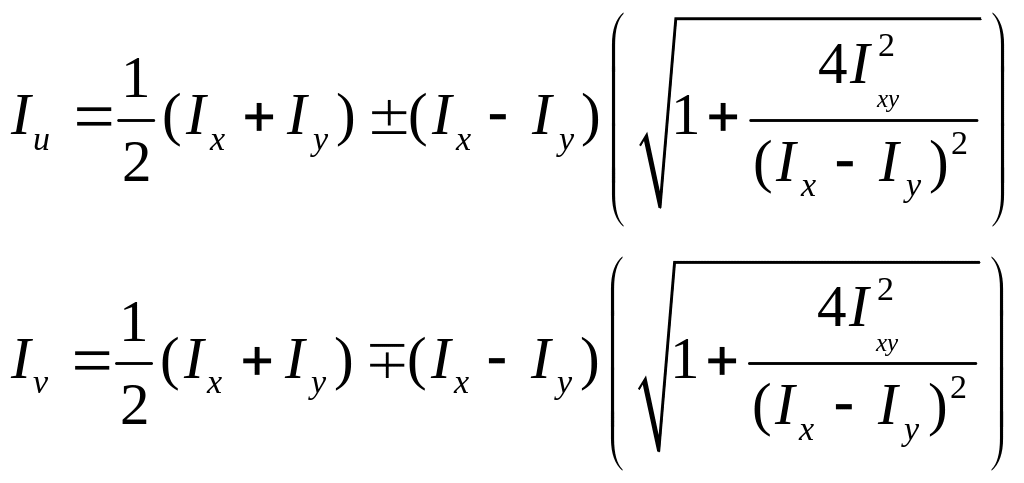
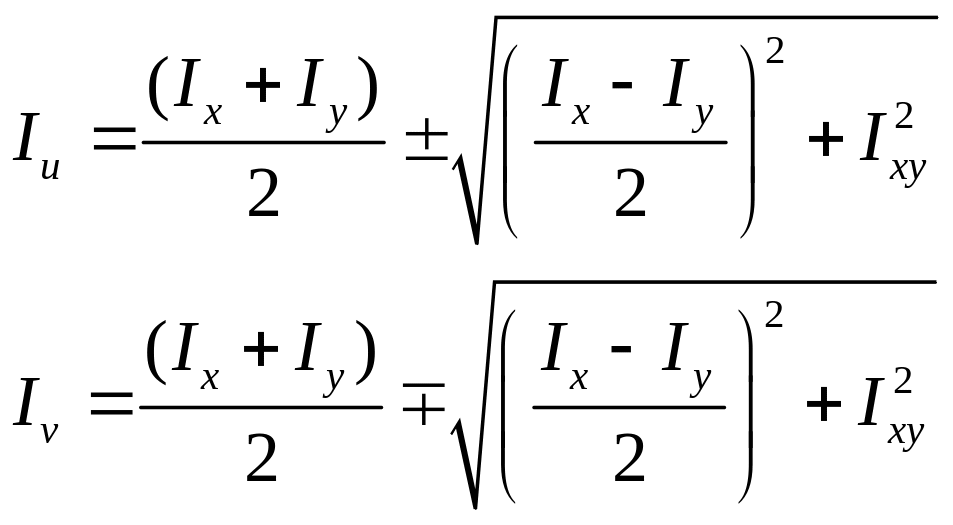
I_x> I_y – первый знак (верхний);

I_y> I_x – нижний знак.

Т.к. оси U и V – главное и центробежные моменты U и V = 0, то

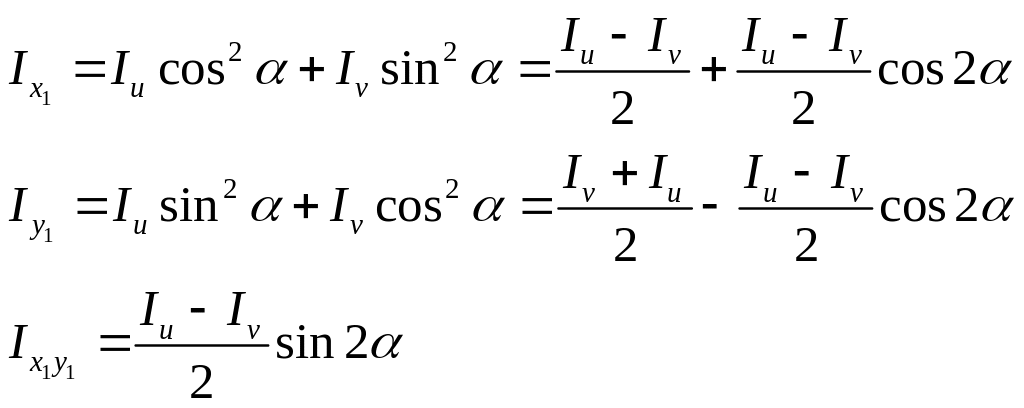
§17. Графическое представление моментов инерции. Круги инерции Отто Мора.

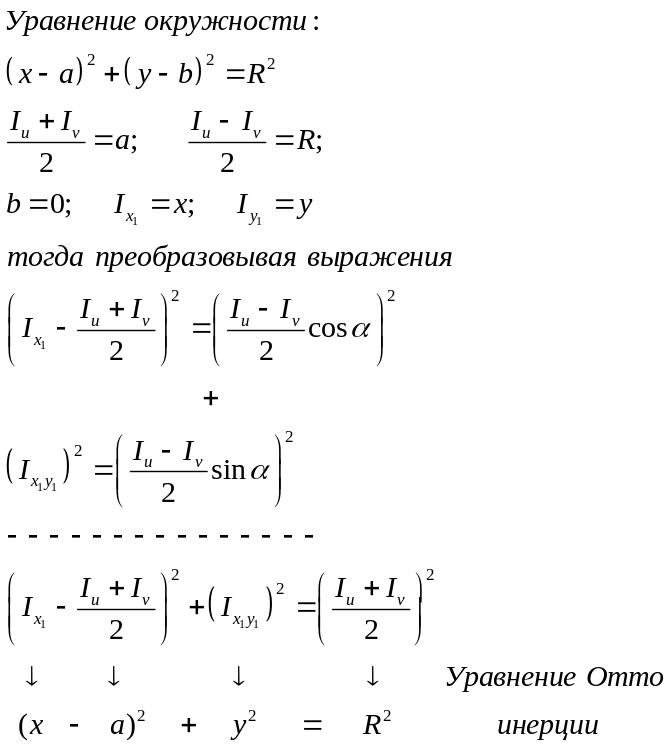
Последовательность построения.

1. Отложим на оси абсцисса отрезки OA = I_u,

OB = I_v

2. Разделим отрезок AB пополам AC=BC

3. Радиусом R=AC=BC проведем окружность.

4. Отложим угол 2α

5 . Dx k_x I_x

D_y k_y I_y

6. Полюс

7 . M_B V

M_A U