К началу страницы

Дифференциальные уравнения высших порядков.

• Дифференциальные уравнения, допускающие понижение порядка.

Порядок дифференциального уравнения  , которое не содержит искомой функции и ее производных до k-1 порядка, может быть понижен до n-k заменой  .

В этом случае  , и исходное дифференциальное уравнение сведется к  . После нахождения его решения p(x) останется вернуться к замене   и определить неизвестную функцию y.

Например, дифференциальное уравнение   после замены  станет уравнением с разделяющимися переменными  , и его порядок с третьего понизится до первого.

Если дифференциальное уравнение не содержит аргумента x, то есть, имеет вид  , то его порядок может быть снижен на единицу заменой  , где p(y(x)) будет сложной функцией. Тогда по правилу дифференцирования сложной функции получим   и так далее.

Подставив эти результаты в исходное уравнение, получаем дифференциальное уравнение не единицу меньшего порядка.

К примеру, дифференциальное уравнение   заменой  приводится к уравнению с разделяющимися переменными  .

Подробное решение подобных примеров представлено в статьедифференциальные уравнения, допускающие понижения порядка.

• Линейные однородные и неоднородные дифференциальные уравнения высших порядков с постоянными коэффициентами и .

Чтобы определить общее решение таких видов дифференциальных уравнений, во-первых, требуется найти корни характеристического уравнения  . В этом Вам может помочь статья решение уравнений высших степеней. Далее, отталкиваясь от значений корней характеристического уравнения, общее решение ЛОДУ   записывается в стандартной форме, а общее решение неоднородного уравнения представляется суммой  , где   - частное решение неоднородного дифференциального уравнения.   можно определить методом вариации произвольных постоянных.

В качестве примера ЛНДУ с постоянными коэффициентами приведем  , ему соответствует ЛОДУ  .

Подробное описание теории и детальный разбор решения примеров смотрите в разделе линейные однородные и неоднородные дифференциальные уравнения высших порядков с постоянными коэффициентами.

• Линейные однородные и неоднородные дифференциальные уравнения высших порядков и .

Общее решение ЛНДУ высших порядков ищется в виде  , где   - общее решение соответствующего ЛОДУ, а   - частное решение неоднородного дифференциального уравнения.

 представляет собой линейную комбинацию линейно независимых функций  , каждая из которых является частным решением ЛОДУ, то есть, обращает равенство   в тождество. Частные решения   обычно подбираются из известных систем линейно независимых функций. Подобрать их далеко не всегда просто и возможно, в этом и заключается основная проблема.

Когда общее решение линейного однородного дифференциального уравнения найдено, частное решение соответствующего неоднородного уравнения можно определить методом вариации произвольных постоянных.

Итак,  .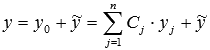

Краткое описание теории приведено в статье линейные дифференциальные уравнения высших порядков.