46. Вынос точки способом линейной засечки. Его точность.

В этом способе положение проектной точки К на местности определяют в пересечении проектных расстояний d₁ и d₂, его применяют в основном для разбивки осей строительных конструкций при d₁ и d₂меньше длины мерного прибора. Одной рулеткой от А откладывают d₁, а рулеткой от точки В отрезок d₂. Пересечение отрезков d₁ и d₂ (при совмещении нулей рулеток с точками А и В) дает определяемую точку К(рис. 1.51).

Рис. 1.51. Линейная засечка

Средняя квадратическая ошибка m_лз линейной засечки при одинаковой точности откладывания отрезков d₁и d₂

                    (1.57)

Величина ошибок исходных данных в линейной засечке

При m_A = m_B = m_AB

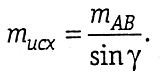
Общая ошибка

                          (1.58)

Средняя квадратическая ошибка откладывания отрезка d = d₁ = d₂

                   (1.59)

При γ =90°, m_к= 10мм, m_АВ = 5 мм находим

47. Вынос точки способом створной засечки. Его точность.

В этом способе положение точки К определяют при пересечении створов Т₁Т'₁ и Т₂Т'₂. Створы на местности задают точками их пересечения с опорными сторонами. Положение точек T₁, Т₂ определяют горизонтальными проложениями d₁ и d₂ от опорной точки В по опорным линиям ВА и ВС, а точек Т'₁, Т'₂ — d'₁, d'₂ от опорной точки Е по линиям EF и ED. Способ пересечения створов (рис. 1.52) обычно используют для выноса в натуру труднодоступных точек, когда использование других методов затруднено.

Рис. 1.52. Пересечение створов

Преимущество этого способа в том, что створы T₁ Т'₁ и Т₂ Т'₂ и точку К легко восстановить, что обеспечивает оперативный контроль точки К в процессе строительства при минимальном объемегеодезических работ.

Средняя квадратическая ошибка М_к положения точки К зависит от средних квадратических ошибок m₁ и m₂определения створов и угла γ, под которым эти створы пересекаются

При m_x = m_y = 5мм, γ = 90° М_к = 7,1 мм

48. Вынос точки способом перпендикуляров. Его точность.

Этот способ обычно применяют в случаях, когда геодезической основой является строительная сетка (рис. 1.46), ее вершины А, В, С, D закреплены на местности. Для выноса точки К (точка сооружения) по линии ADоткладывай ют отрезок d₁ = У_К - У_А и по перпендикулярному AD направлению отрезок d₂ = Х_к - Х_А. Для построения отрезков и d₂ теодолит устанавливают над точкой А и приводят его в рабочее положение. Перекрестие нитей зрительной трубы наводят на точку D и от точки А в створе линии AD, фиксируемой теодолитом, откладывают горизонтальное проложение d₁ и получают точку Р. Теодолит переносят и устанавливают над точкой Р, приводят его в рабочее положение, откладывают прямой угол APР'. По направлению РР' от точки Р откладывают горизонтальное проложение d2, получают точку К, закрепляют ее.

Рис. 1.46. Способ прямоугольных координат

Средняя квадратическая ошибка положения точки К выражается формулой

             (1.42)

где m _Δх, m _Δy — средние квадратичеcкие ошибки откладывания приращения координат; m_β — средняя квадратическая ошибка построения угла в точке Р; m²_исх, m²_ц, m²_ф — средние квадратические ошибки исходных данных, центрирования теодолита и фиксации точки К соответственно. Центрирование теодолита и фиксирование точки обычно равны m_ц = m_ф = 1 мм. При стороне строительной сетки 200 м и положении точки К в середине квадрата (Δх = Δу = 100 м) и при относительной ошибке откладывания Δх и Δу 1:10 000 получим m_Δx = m_Δу = 100 000/10 000 = 10 мм. При m_β = 10" (mβ / ρ) Δx = 10" · 100 000 / 206 265" = 5 мм,    m_ф= 1 мм.

Принимая m_исх = 10 мм, по формуле (1.42) находим

 Значения m_ц и m_ф по малости можно не учитывать.