Вектор направлен согласно правилу векторного произведения (рисунок 20, б).
Модуль абсолютного ускорения точки находим способом проекций:
.
Результаты расчёта сведены в таблицу 11.
Таблица 11
|
Скорость, см/с |
|
Ускорение, см/с2 |
||||||||||
|
|
|
|
|
|
аrn |
arτ |
ac |
ax |
ay |
az |
a |
|
–0,93 |
9,3 |
65,2 |
65,9 |
–10,2 |
9 |
102 |
0 |
–355 |
61 |
163 |
–186 |
308 |
395 |
Динамика
5. Интегрирование дифференциальных уравнений движения материальной точки, находящейся под действием постоянных сил
Варианты 1–5
(рисунок 21, схема 1). Тело движется из
точки
по участку
(длинной l) наклонной
плоскости, составляющей угол
с горизонтом, в течение
,
с. Его начальная скорость а.
Коэффициент трения скольжения тела по
плоскости равен
.
В точке
тело покидает плоскость со скоростью
и попадает со скоростью
в точку
плоскости
,
наклонённой под углом
к горизонту, находясь в воздухе
с.
При решении задачи тело принять за материальную точку, сопротивление воздуха не учитывать.
В.1. Дано:
;
;
;
;
.
Определить
В.2. Дано:
;
;
;
;
.
Определить уравнение траектории точки
на участке
и
.
В.3. Дано:
;
;
;
;
;
.
Определить:
,
.
В.4. Дано:
;
;
;
.
Определить , .
В.5. Дано:
;
;
;
.
Определить
.
Варианты 6-10
(рисунок 21, схема 2). Лыжник подходит к
точке
по участку трамплина
(длинной l),наклонной
плоскости, составляющей угол
с горизонтом, в течение
,
с. Его начальная скорость
.
Коэффициент трения скольжения лыж на
участке
равен
.
В точке
он покидает трамплин со скоростью
.
Через Т с лыжник приземлится и
попадает со скоростью
в точку
горы, наклонённой под углом
к горизонту.
При решении задачи тело лыжника принять за материальную точку и сопротивление воздуха не учитывать.
В.6. Дано:
;
;
;
.
Определить
,
.
В.7. Дано:
;
;
;
;
.
Определить
и Т.
В.8. Дано:
;
;
;
Определить
.
В.9. Дано:
;
;
;
.
Определить
и
.
В.10. Дано:
;
;
;
;
.
Определить
и уравнение движения лыжника;
Варианты 11-15
(рисунок 21, схема 3). Мотоциклист движется
из точки
со скоростью
по участку дороги
(длинной l) наклонной
плоскости, составляющей угол
с горизонтом, в течение
,
с. При постоянной на всём участке
движущей силе
мотоцикл в точке
приобретает скорость
и перелетает через ров шириной
,
находясь в воздухе
с и приземляясь в точке
со скоростью
.
Масса мотоцикла с мотоциклистом равна
.
При решении задачи мотоциклиста принять за материальную точку: сопротивление движению не учитывать.
В.11. Дано:
;
;
;
;
;
.
Определить:
и
h.
В.12. Дано:
;
;
;
;
.
Определить:
,
.
В.13. Дано:
;
;
;
.
Определить:
,
.
В.14. Дано:
;
;
;
;
.
Определить:
;
.
В.15. Дано:
;
;
;
;
;
.
Определить:
,
.
Варианты 16-20 (рисунок 21, схема 4). Камень скользит в течение с из точки по участку (длинной l) откоса, составляющей угол с горизонтом. Его начальная скорость . Коэффициент трения скольжения камня по откосу равен .
В точке камень покидает откос со скоростью и попадает в точку вертикальной защитной стены, находясь в воздухе Т с ударяется в точке о вертикальную защитную стену.
При решении задачи камень принять за материальную точку: сопротивление воздуха не учитывать.
В. 16. Дано:
;
;
;
;
.
Определить
и
.
В. 17. Дано:
;
;
;
.
Определить и .
В. 18. Дано:
;
;
;
;
.
Определить и .
В. 19. Дано:
;
;
;
.
Определить и .
В. 20. Дано:
;
;
;
.
Определить и .
Варианты 21-25 (рисунок 21, схема 5). Тело движется из точки А по участку АВ (длиной ) наклонной плоскости, составляющей угол с горизонтом. Его начальная скорость . Коэффициент трения скольжения равен . Через с тело в точке со скоростью покидает наклонную плоскость и падает на горизонтальную плоскость в точку со скоростью ; при этом оно находится в воздухе Т с.
При решении задачи принять тело за материальную точку и не учитывать сопротивление воздуха.
В. 21. Дано:
;
;
;
.
Определить и .
В. 22. Дано:
;
;
;
.
Определить и уравнение траектории на участке .
В. 23. Дано:
;
;
;
;
.
Определить и Т.
В. 24. Дано:
;
;
;
;
.
Определить и .
В. 25. Дано:
;
;
;
;
.
Определить и .
Варианты 26-30 (рисунок 21, схема 6). Имея в точке А скорость , тело движется по горизонтальному участку длиной в течение с. Коэффициент трения скольжения тела по плоскости равен . Со скоростью тело в точке покидает плоскость и попадает в точку со скоростью , находясь в воздухе Т с. При решении задачи принять тело за материальную точку; сопротивление воздуха не учитывать.
В. 26. Дано:
;
;
;
.
Определить и .
В. 27. Дано:
;
;
.
Определить и .
В. 28. Дано:
;
;
;
.
Определить и Т.
В. 29. Дано:
;
;
;
.
Определить и .
В. 30. Дано:
;
;
;
.
Определить и .
Рисунок 21
Пример выполнения
задания (рисунок 22). В железнодорожных
скальных выемках для защиты кюветов от
попадания в них с откосов каменных
осыпей устраивается «полка»
.
Учитывая возможность движения камня
из наивысшей точки
и полагая при этом его начальную скорость
,
определить наименьшую ширину полки b
и скорость
,
с которой камень падает на нее. По участку
откоса, составляющему угол
с горизонтом и имеющему длину
,
камень движется
с.
При решении задачи считать коэффициент трения скольжения камня на участке постоянным, а сопротивлением воздуха пренебречь.
Дано:
;
;
;
;
;
.
Определить
и
.
РЕШЕНИЕ:
Рассмотрим движение камня на участке
.
Принимая камень за материальную точку,
покажем (рисунок 22) действующие на него
силы: вес
,
нормальную реакцию
и силу трения скольжения
.
Составим дифференциальное уравнение
движения камня на участке АВ:
;
Сила трения
где
.
Таким образом,
.
или
.
Интегрируя дифференциальное уравнение дважды, получаем
;
.
Для
определения постоянных интегрирования
воспользуемся начальными условиями
задачи: при
и
.
Составим уравнения, полученные при интегрировании, для :
;
.
Найдем постоянные:
,
.
Тогда
;
.
Для момента , когда камень покидает участок,
;
,
т.е.
;
,
откуда
,
т.е.
Рассмотрим движение камня от точки до точки .
Показав силу тяжести , действующую на камень, составим дифференциальные уравнения его движения :
;
.
Начальные условия задачи: при t = 0
,
;
;
.
Интегрируем дифференциальные уравнения дважды:
;
,
,
.
Напишем полученные
уравнения для
:
;
;
;
.
Отсюда найдем, что
;
;
;
.
Получим следующие уравнения проекций скоростей камня:
;
;
и уравнения его движения:
;
;
Уравнение траектории
камня найдем, исключив параметр
из уравнений движения. Определим
из первого уравнения и подставив его
значение во второе, получаем уравнение
параболы:
.
В момент падения
определяя
из уравнения траектории, найдем
,
.
Так как траекторией движения камня является ветвь параболы с положительными абсциссами ее точек, то .
Минимальная ширина полки
,
или
.
Используя уравнение
движения камня
,
найдем время Т движения камня от
точки
до точки
:
Скорость камня при падении найдем через проекции скорости на оси координат
; ;
по формуле
.
Для момента падения
,
или
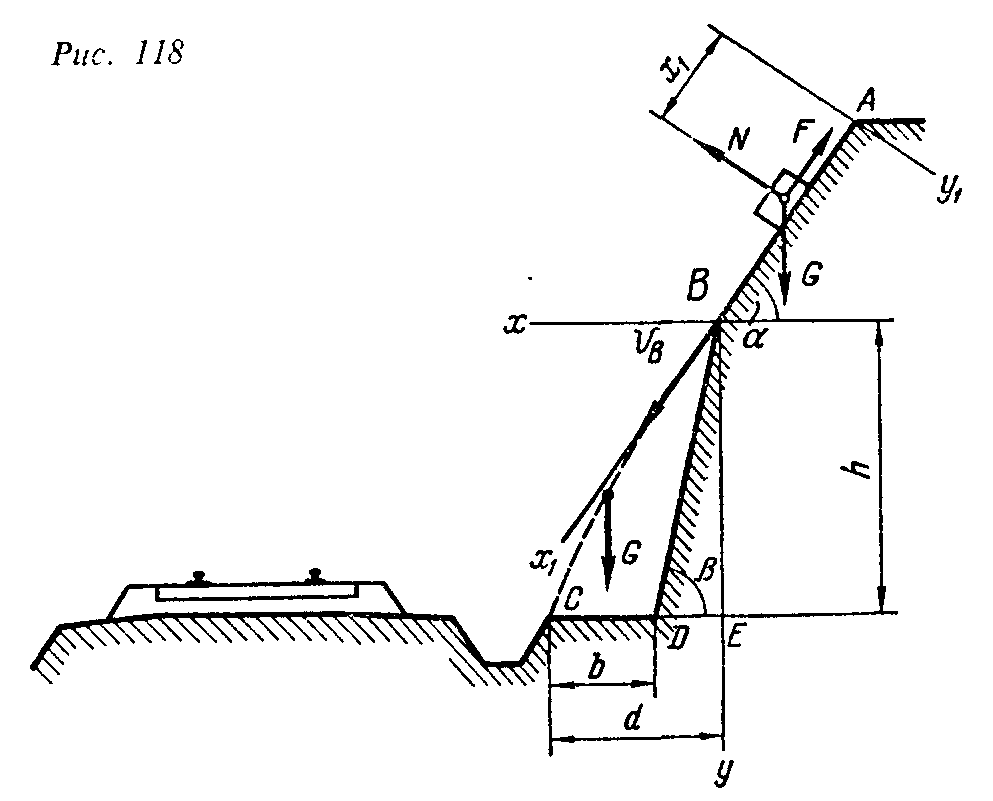
Рисунок 22
Приложение 1
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
ГЕОРГИЕВСКИЙ ТЕХНОЛОГИЧЕСКИЙ ИНСТИТУТ (филиал)
СЕВЕРО-КАВКАЗСКОГО ГОСУДАРСТВЕННОГО ТЕХНИЧЕСКОГО
УНИВЕРСИТЕТА
Кафедра МиЕНД
КУРСОВОЙ ПРОЕКТ
ПО «ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ»
НА ТЕМУ: «РЕШЕНИЕ ЗАДАЧ СТАТИКИ, КИНЕМАТИКИ И
ДИНАМИКИ»
Выполнил :___________________
_____________________________
Проверил:____________________
Проект защищен «___»______________200_г
с оценкой «______________________»
Преподаватель:________________________
Георгиевск, 200_