Модуль нормального ускорения точки

(7)

Если радиус кривизны траектории в рассматриваемой точке неизвестен, то можно определить по формуле:

. (8)

При движении точки в плоскости формула (8) принимает вид:

(8')

Модуль нормального ускорения можно определить и следующим образом:

. (9)

После того, как найдено нормальное ускорение по формулам (8) или (9), радиус кривизны траектории в рассматриваемой точке определяется из выражения:

(10)

Результаты вычислений по формулам (3 –6), (8) и(10) для заданного момента времени приведены в таблице 9.

Таблица 9

х	у	vх	vу	v	ах	ау	а	аτ	ап	ρ
2,0	3,0	4,0	16,0	16,5	0	32,0	32,0	31,0	7,8	35,0

На рисунке 15 показано положение точки в заданный момент времени. Вектор строим по составляющим, Причём этот вектор должен по направлению совпадать с касательной к траектории. Вектор строим по составляющим и и затем раскладываем на составляющие и . Совпадение величин и найденных из чертежа, с их значениями, полученными аналитически, служит контролем правильности решения.

Рисунок 15

4. Определение абсолютной скорости и абсолютного ускорения точки

Точка М движется относительно тела D. По заданным уравнениям относительного движения точки M и движения тела D определить для момента времени t=t₁ абсолютную скорость и абсолютное ускорение точки М. Схемы механизмов показаны на рисунках 17 – 19. А необходимые для расчёта данные приведены в таблице 10.

Пример выполнения задания: Дано: схема механизма рисунок 19,

;

РЕШЕНИЕ: Будем считать, что в заданный момент времени плоскость чертежа рис.16 совпадает с плоскостью треугольника D. Положение точки М на теле D определяется расстоянием

При

Абсолютную скорость точки М найдём как геометрическую сумму относительной и переносной скоростей:

.

Модуль относительной скорости:

;

где

;

при

; .

Рисунок 16

Рисунок 17

Рисунок 18

Рисунок 19

Таблица 10

Номер варианта	Уравнение относительного движения точки М	Уравнение движения тела		t1, см	R, см	а, см	α, град	Дополнительные данные
1			-	2/3	-	25	-
2			-	5/3	20	-	-
3			-	2	-	30	-
4			-	1	-	-	60
5			-	2	30	-	-
6	-	-		10/3	15	-	-
7			-	3/8	-	40	60
8			-	2	-	-	30
9			-	1/8	-	-	-
10			-	4/3	20	20	-
11			-	4	-	25	-
12			-	2	30	30	-
13			-	1/3	40	-	-
14			-	2/3	-	-	30
15			-	2	-	60	45
16			-	1/3	-	20	-
17			-	1	-		-
18			-	2	-	-	60
19			-	2	40	-	-
20			-	3	60	-	-
21			-	1/2	25	-	-
22			-	2/3	30	-	-
23		-	-	1	18	-	-	О1О=О2А=20cм
24			-	1	30	-	-
25			-	5	-	-	-
26			-	3/2	-	-	45
27	-	-		2	75	-	-
28			-	2	40	-	-
29		-	-	2	30	-	-	О1О=О2А=40cм
30		-		2	48	-	-

Примечание к таблице 10: Для каждого варианта положение точки М на схеме соответствует положительному значению s_r; в вариантах 5, 10, 12, 20-24, 28-30 – дуга окружности; на схемах 5,10,12,21,24 ОМ – дуга, соответствующая меньшему центральному углу. Относительное движение точки М в вариантах 6 и 27 и движение тела D в вариантах 23 и 29 определяется уравнениями, приведёнными в последнем столбце таблицы 10.

Положительный знак у показывает, что вектор направлен в сторону возрастания _. Модуль переносной скорости:

, (1)

где – радиус окружности , описываемой той точкой тела, с которой в данный момент совпадает точка , ; модуль угловой скорости тела:

При

;

Отрицательный знак величины показывает, что вращение треугольника происходит вокруг оси вниз (рисунок 20,а).

Модуль переносной скорости, по формуле (1)

Вектор направлен по касательной к окружности в сторону вращения тела. Так как вектора и взаимно перпендикулярны, модуль абсолютной скорости точки

_.

или

.

Абсолютное ускорение точки равно геометрической сумме относительного, переносного и кориолисова ускорений:

,

или в развёрнутом виде:

,

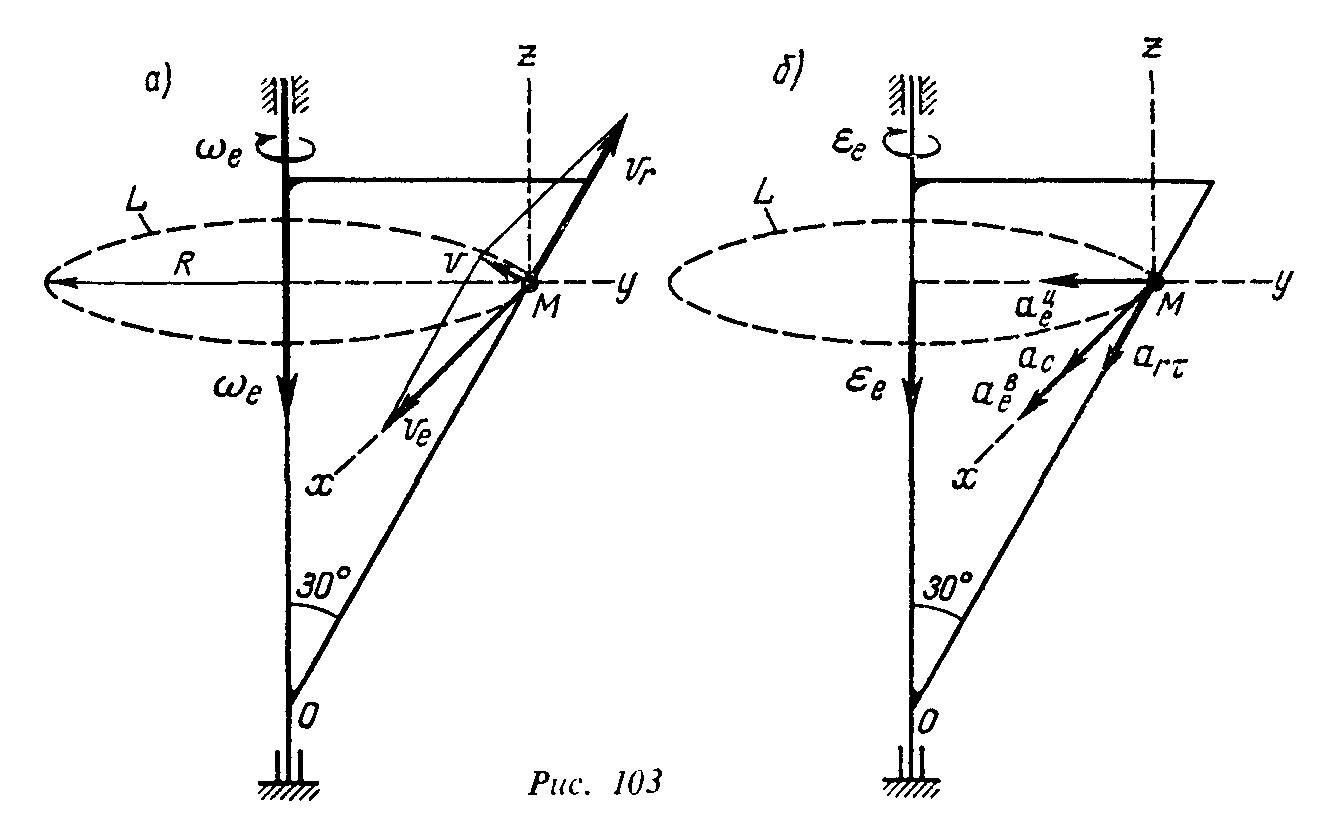
Рисунок 20

Модуль относительного касательного ускорения:

;

где

При

, .

Отрицательный знак показывает, что вектор направлен в сторону отрицательных значений .Знаки и одинаковы: следовательно, относительное движение точки ускоренное.

Относительное нормальное ускорение:

,

так как траектория относительного движения – прямая .

Модуль переносного вращательного ускорения

, (2)

где - модуль углового ускорения тела :

.

При

, .

Знаки и одинаковы; следовательно, вращение треугольника D ускоренное, направления векторов и совпадают (рисунки 20 а, б)

Согласно (2):

вектор направлен в туже сторону, что и .

Модуль переносного центростремительного ускорения

или .

Вектор направлен к центу окружности L.

Кориолисово ускорение

,

модуль кориолисова ускорения

,

где

.

С учётом найденных выше значений и , получаем

.