3.5 Затухание плоских волн в среде с потерями

В диэлектрической среде всегда возникает затухание электромагнитных волн, вызванное потерями в диэлектрике. Затухание оценивается спадом амплитуды поля по мере изменения координаты вдоль направления распространения волны. Диэлектрическая среда с потерями характеризуется комплексной диэлектрической проницаемостью . Поэтому постоянная распространения электромагнитной волны в среде с потерями становится комплексной величиной

После подстановки в случае малых потерь получим

(3.19)

Поэтому соотношение для плоской волны (3.10) изменится и примет вид

(3.20)

Как видно из (3.20) фазовый множитель определяется вещественной частью постоянной распространения, а амплитуда волны экспоненциально спадает с ростом z. Величину называют коэффициентом затухания. Количественной мерой затухания выбирают относительный спад волны на длине L. Из (3.20) следует, что

В инженерной практике значение коэффициента затухания принято оценивать либо в Неперах (Нп) либо в децибелах (дБ) в соответствии с соотношением

Коэффициент затухания обычно приводят к единицы длины распространения волны.

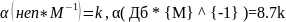
При малом затухании вещественная часть постоянной распространения незначительно отличается от постоянной распространения в среде без затухания. В свою очередь можно считать пропорциональной частоте, как это следует из (3.19). Поэтому существенных отличий от плоской незатухающей волны при нет.

Ситуация кардинально меняется в проводящей среде. В соответствии с (3.2) диэлектрическую проницаемость проводящей среды можно считать равной

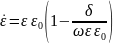
Поэтому, постоянная распространения в ней принимает следующий вид

(3.21)

Для проводников мнимый член в (3.21) вплоть до частот оптического диапазона.

У меди =5*10 7 . Поэтому с исчезающее малой ошибкой можно считать, что

На частоте

Поэтому (3.22)

Введем величину имеющую размерность длины и представим постоянную распространения в эквивалентном виде

Затухание волны определяется мнимой частью k и плоская волна может быть записана в виде

(3.23)

Соотношения между амплитудами напряженностей электрического и магнитного поля в плоской волне в диэлектрике определяется соотношением (3.13). В проводящей среде оно изменяется и становится равным

(3.24)

Из 3.24 следует, что в проводящей среде в плоской волне возникает фазовый сдвиг между электрически и магнитным полем равный . Как показывает соотношение (3.23) волна экспоненциально затухает с расстоянием. Найдем глубину проникновения поля в металл полагая, что z=0 соответствует поверхности металла, на которую по нормали (по оси z) падает плоская волна. Тогда на расстоянии от поверхности равном Δ амплитуда спадает в e раз. Это расстояние называется глубиной проникновения в металл и глубиной скин слоя

(3.25)

Принято считать, что поле в металле существует только в скин слое, а вне его равно нулю. Значение на частоте 10 для меди составляет 0.7 мкм. Как видно из (3.25) дельта стремится к нулю если проводимость стремится к бесконечности и уменьшается с ростом частоты.

В проводниках магнитное поле велико по сравнению с электрическим. Как следует из (3.24) отношение амплитуд магнитного поля и электрического много больше 1

Таким образом при распространении волны в металле энергия не разделяется поровну между полями E и H как это существует в незатухающей волне. Плотность электрической энергии пренебрежимо мала по сравнению с магнитной, иначе говоря, электрическое поле почти не приникает в металл, при стремящемся к бесконечности оно равно нулю уже на поверхности металла. Это обстоятельство нашло отражение в граничных условиях на поверхности идеального металла (Раздел 2.4). Для металла с конечной, но большой проводимостью, граничное условие для касательной составляющей электрического поля к его поверхности может быть задано соотношением, которое следует из (3.24)

где поле на поверхности металла орт к нормали поверхности. Полагая, что z нормальна к поверхности металла запишем соотношение для в виде

Магнитное поле в этих соотношениях определено со стороны диэлектрика на поверхности металла. Оно проникает в металл и определяет электрическое поле на поверхности металла при конечной проводимости.