3.2 Вектор Пойнтинга для гармонических полей
Метод описания гармонических полей с помощью комплексных величин, соотнесенных полям E и H, нельзя применить к нелинейным величинам. Одно из них в теории поля является вектор Пойнтинга (2.3). Заменив в (2.3) E и H на E и H, нельзя считать, что вектор Пойнтинга S реальной части , т.е,
Для гармонических полей практический интерес представляет усредненный по времени поток энергии или вектор Пойнтинга
Найде S и Sср. Для этого представим истинные поля в S через очевидные тождества где E и H комплексно сопряженные величины. Тогда вектор Пойнтинга равен
Это соотношение определяет мгновенные значения плотности энергии гармонического поля. При усреднении по времени векторный характер S не играет роли. Поэтому, в интеграле для Sср можно заменить S на его модуль, который по определению равен
В этом соотношении можно опустить начальные фазовые сдвиги в E и H. Тогда произведение
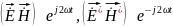
и при усреднении по периоду они обнуляются. В S остаются только произведения
Поэтому возвращаясь к векторной форме найдем, что
Таким образом, среднее значение вектора Пойнтинга можно определить как
где
- комплексный вектор Пойнтинга.
Если сохранить начальные фазовые сдвиги в E и H, то
3.3 Волновые уравнения для гармонических полей. Плоские волны.
Одним из высших достижений Максвелла оказалось то, что на основе его уравнений, можно было предвидеть существование электромагнитных волн, несущих энергию, и скорость которых можно было определить из теоретических соображений. Уравнения Максвелла для гармонических полей в неограниченном пространстве имеют вид, определенные соотношениями (3.2). Будем искать решения уравнений для свободного пространства . Из уравнений (3.2) следует, что напряженности полей должны удовлетворять следующим уравнениям
(3.7)
где
–
постоянная распространения или волновой
число плоской волны в свободном
пространстве. На основании векторного
анализа
где
– произвольный вектор, ∇
- оператор Лапласа (Лапласиан) примененный
к вектору
.
Так как в свободном пространстве дивергенция E равна нулю, а дивергенция H равна нулю всегда, то каждое уравнение в (3.7) можно преобразовать к виду
(3.8)
Уравнения (3.8) называются волновыми для гармонических полей. Они эквивалентны для уравнений Максвелла в том смысле, что их решения, являются решениями уравнений Максвелла.
В
общем случае вектора напряженностей
поля E и H
могут иметь по три компоненты. Например,
в декартовой системе координат
. Уравнения (3.8)
справедливы для каждой компоненты E
и H.
Волновое уравнение имеет известное
решение в виде плоской волны. В плоской
волне напряженности полей зависят
только от расстояний координат и
плоскостью нормальной к направлению
распространения. Выберем направление
распространения плоской волны вдоль
оси z. В этом случае
плоскостью нормальной к оси z,
является координатная плоскость X0Y,
в которой по определению плоской волны
, а
. Тогда из условий DivE=0
DivH=0, следует, что
. Но производные не могут быть
равны нулю, так как в этом случае все
три производные равны нулю. Поэтому
должны быть равны нулю продольные
составляющие напряженности поля
(проекция на направления распространения)
. Следовательно электромагнитное
поле плоской волны имеет поперечный
характер: векторы E и H
лежат в плоскости X0Y
рис.3.1 и нормальны к оси z.
В уравнении (3.2.а) можно заменить rotE
на эквивалентную запись
. Но так как в плоской волне
то уравнение (3.2.а) преобразуется
к виду
Отсюда следует, что
(3.9)
Согласно (3.9) вектор
перпендикулярен (нормален) плоскости,
образованной ортом и
,
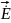следовательно
и
перпендикулярны друг другу и вместе с
ортом ez
образуют правую ортогональную систему
векторов.
Не
теряя общности положим, что в плоскости
X0Y вектор
E ориентирован вдоль оси
x т.е. . Тогда из (3.9)
следует, что
.
Перейдем к решению волновых уравнений (3.8). Для плоской волны оператор Лапласа
и уравнения (3.8) принимают вид
Они имеют формально векторный характер так как и заданы единственными компонентами. Решения уравнений хорошо известны. Поэтому запишем их в виде
(3.10)
где
произвольные комплексные
амплитуды. Перейдем от комплексной
формы напряженностей полей к истинным
полям. Выберем первые слагаемые в (3.10)
и найдем напряженности поля как
Положим начальные фазы в E и H равными нулю и преобразуем E и H к виду
(3.11)
Из (3.11) следует, что одинаковые значения фазы косинуса возникают с изменением времени на величину Δt при изменении координаты z на Δz:
откуда получаем, что
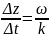Это
равенство можно истолковать единственным
образом как скорость перемещения
фиксированного значения фазы поперечной
волны вдоль направления распространения.
Она называется фазовой скоростью
поперечной волны и равна
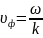
С
учетом того, что
находим, что в свободном пространстве
а в
среде с относительными проницаемостями
ε, ϻ волна замедляется в
раз . Соотношение (3.11) позволяет
установить пространственную периодичность
волны. Наименьшее расстояние между
точками с одинаковыми фазами в данный
момент времени называется длиной волны
λ . Из (3.11) следует соотношение для
определения λ
откуда
(3.12)
Вернемся
к соотношению (3.10) вторые слагаемые в
нем отличаются показателями степени.
Это означает, что фазовый набег тех же
значений достигается при равных, но
отрицательных z. Это дает
основание считать вторые слагаемые в
(3.10) волнами, распространяющимися в
направлении отрицательных значений z.
На основании (3.9) и (3.10) можно установить
соотношения для амплитуд напряженностей
электрического и магнитного поля в
поперечной плоской волне как
. Число
имеет размерность (Ом) и называется
волновым сопротивлением свободного
пространства. В среде с относительными
проницаемостями волновое сопротивление
равно
. Учитывая взаимную
ориентацию E и H
и направление распространения волны
запишем
(3.13)
Мгновенный вектор Пойнтинга S на основании (2.23), (3.11) и (3.13) равен
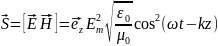
(3.14)
Вектор Пойнтинга в виде (3.14) определяет мгновенную плотность потока энергии переносимую плоской волной, а средняя плотность энергии равна
Найдем мгновенной значение объемной плотности энергии в плоской волне. Для этого подставим в (2.22) соотношения (3.13), положив и получим
Подставим в (2.18) соотношения для w , соотношения для мгновенного вектора Пойнтинга (3.14) и найдем скорость переноса энергии плоской волной
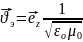
Как видно она в свободном пространстве совпадает со скоростью света.
В заключении подведем краткий итог этого раздела. В свободном пространстве электромагнитное поле существует в виде плоской волны. Это значит, что поверхность равных фаз является плоскостью. В наше случае z=const. В каждый момент времени фаза поля согласно (3.11) постоянна в плоскости z=const. Плоскость равных фаз называют фронтом волны. С течением времени фронт волны перемещается вдоль оси перпендикулярный плоскости равных фаз, со скоростью света в свободном пространстве. Тройка векторов, определяющая пространственное положение E , H и направление распространения и образует правовинтовую ортогональную систему. Идеальная плоская волна, является не более чем модельным представлением реального поля, которое на большом удалении от источника должно иметь сферических характер. В сферической волне продольные составляющие напряженностей электрического или магнитного поля (вдоль направления радиуса) затухают пропорционально где r расстояние от источника излучения. Поэтому на большом удалении от источника ее можно считать равной нулю. Это дает основание заменить участок сферического фронта реальной волны на локальный плоский фронт. Благодаря большому удалению от источника излучения с исчезающее малой ошибкой можно считать, что поток энергии падает на эту плоскость параллельным пучком. Следовательно, по отношению к источнику все точки локальной плоскости равноправны и электромагнитное поле в ней постоянно, что соответствует определению идеальной плоской волны.