6.8 Дифракция на круглом отверстии в проводящем экране

Рассмотрим в качестве еще одного примера дифракцию плоской волны на круглом отверстии в проводящем экране. Сохраним координатную систему предыдущей задачи, в которой плоская волна с вектором поляризации в плоскости падения падает нормально на проводящий экран с круглым отверстием диаметром 2а. Координатная система представлена на рис.6.10 с тем отличием, что в пределах отверстия задана полярная система координат: - полярная координата, - полярный угол произвольной точки на отверстии. Электрическое и магнитное поле в падающей волне представим в декартовых координатах в виде

В пределах отверстия (z=0) поле постоянно и равно

При расчете дифракционного поля с помощью соотношений (6.50) или (6.50*) предварительно надо вычислить электродинамические потенциалы, определенные соотношениями (6.51). В дальней зоне, зависимость потенциалов от координат отверстия можно сохранить только в фазовом множителе , так как при диаметре отверстия сравнимым с длиной волны, разностью фазовых сдвигов в точке наблюдения от отдельных точек на отверстии пренебречь нельзя. В предшествующих разделах это подробно обсуждалось. Поэтому положим, что под интегралом в (6.51) в числителе , а в знаменателе . Целью расчета является угловая зависимость дифракционного поля. В силу азимутальной симметрии задачи, дифракционное поле имеет одинаковую зависимость в плоскостях E и H. Вычислим поле в E плоскости, положив =0. Запишем соотношения между декартовыми, полярными и сферическими координатами. В пределах отверстия . В E плоскости в соответствии с (6.53*) декартовые и сферические координаты точки наблюдения, связаны соотношением . Следовательно в соответствии с (6.51*)

Представим интеграл по отверстию (6.52) в виде

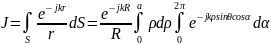
(6.58)

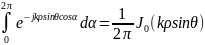
Интеграл по углу в (6.58) вычисляется точно, где 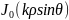- функция Бесселя.

Интеграл по радиусу в (6.58) равен

(6.59)

Таким образом, угловая зависимость дифракционного поля в дальней зоне в E и H плоскостях от круглого отверстия определяется функцией

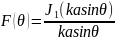
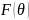Если отверстие велико по сравнению с длиной волны ( ), то имеет острый максимум равный единице при и быстро спадает до нуля. Угловая ширина зоны излучения в пределах первого нуля функции определяется значением первого корня функции Бесселя первого порядка

Таким образом, в коротковолновом приближении, поле в основном проходит через отверстие и дифракционные эффекты малы.