5.10 Коаксиальные волноводы

Исследуем возможность передачи электромагнитной энергии вдоль волновода, представляющего собой два коаксиальных металлических цилиндра рис.5.13. В отличии от ранее рассмотренных волноводов, поперечное сечение коаксиального волновода представляет собой двухсвязанную область. Как было показано в разделе 5.1 в двухсвязанной направляющей структуре могу распространятся волны TEM типа. Для этих волн волновое уравнение тождественно совпадает с уравнением Лапласа и следовательно на поперечном сечении коаксиального волновода поле распределено как в цилиндрическом конденсаторе. Так как TEM волны подчиняются квазистатическому описанию, то они допускают описание с помощью тока и напряжения. Очевидно, что в коаксиальном волноводе может течь ток вдоль обоих цилиндров, а между ними возникает разность потенциалов. На основании этой особенности, коаксиальный волновод, называют линией передачи. Поэтому любую волноведущую структуры допускающую возможность существования TEM волны относят к линиям передач. Помимо коаксиальной линии в инженерной практике применяются двухпроводные линии и разнообразные полосковые линии. В линиях передачи основным типом волны, является TEM волна, у которой критическая длина волны равна бесконечности, а граничная частота равна нулю. На высоких частотах в линиях передачи могут возникнуть условия появления высших типов TE, TM и гибридных типов волн. Поэтому анализ линии передачи с TEM полем всегда должен сопутствовать анализ волн высших типов, результатом которого, являются условия одномодовости TEM волны.

Рассмотрим TEM волну в коаксиальной линии. Магнитное поле волны является решением уравнения Лапласа для прямолинейного круглого провода, которое было получено в разделе 1.3 соотношение (1.23). Для электромагнитного поля оно может быть записано в виде

где Im амплитуда тока в цилиндре, r – координата точки на поперченном сечении коаксиальной линии рис.5.13. Отношение поперечных компонент электрического и магнитного поля в TEM волне равно раздел 3.3 соотношение (3.13). Поэтому напряженность электрического поля запишем в виде

Для линий передачи вводят понятие волнового сопротивления линии, которое определяется отношением амплитуды напряжения к амплитуде тока. Напряжение вычисляется как интеграл по произвольному пути между цилиндрами. Поэтому проинтегрируем E воль силовой линии поля

(5.81)

По определению волновое сопротивление равно

Поэтому из (5.81) найдем, что

В том случае если пространство между цилиндрами коаксиальной линии заполнено диэлектриком с относительной диэлектрической проницаемостью  то волновое сопротивление будет равно

Найдем условие существования волн H типа в коаксиальном волноводе. Решение волнового уравнения (5.7.б) относительно продольной составляющей магнитного поля в пространстве между цилиндрами имеет вид

где – функция Неймана .

Налагая граничные условия для Hz на поверхностях внутреннего и внешнего цилиндра

получим однородную систему уравнений относительно пары неизвестных.

Где

Отсюда следует уравнение относительно постоянной распространения γ.

Корни уравнения известны и приводятся в справочниках. Очевидно они соответствуют разным типам полей. Как и волом круглом волноводе, наибольшую критическую длину имеет волна H11 типа. ЕЕ численная оценка близка к длине средней окружности

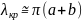
Среди волн электрического типа, является азимутально симметричная волна E01 с критической длиной волны близкой к .

6. Излучение и дифракция электромагнитных волн

6.1. Электродинамические потенциалы

В предшествующих главах мы рассмотрели электромагнитные поля в свободном пространстве и в волноведущих структурах вне связи с переменными зарядами и токами, которые являются источниками поля. Поэтому волновые уравнения были однородными, а их решения имели характер общего решения дифференциального уравнения. Сей час мы рассмотрим излучение волн в свободное пространство с помощью простейших излучающих систем. Возможность излучения электромагнитного поля, следует непосредственно из закона сохранения энергии в форме соотношения (2.27): уменьшение электромагнитной энергии в ограниченном объеме пространства при отсутствии в нем потерь равно потоку энергии (излучению) через поверхность ограничивающую объем.

Уравнения Максвелла можно преобразовать к однородным волновым уравнениям с правыми частями, являющимися функциями тока и заряда. Однако в этом случае даже для простых излучающих систем, решения уравнений связаны с большими математическими трудностями. Однако связь полей излучения с током и зарядом, можно установить опосредованно с помощью вспомогательных функций, которые называются электродинамическими потенциалами: векторным и скалярным. Электрическое поле нельзя выразить только через скалярный потенциал, как это возможно в электростатическом поле, так как в следствии закона индукции . Магнитное же поле можно выразить через произвольный вектор А с помощью соотношения

(6.1)

но так как , а дивергенция ротора равна нуль по определению.

Соотношение (6.1) вводит векторный потенциал А для магнитостатического и переменного магнитного полей. Далее мы рассматриваем только гармонические электромагнитные поля, поэтому запишем (6.1) в комплексном представлении пологая, что , и для свободного пространства (6.1) записывается в виде

(6.2)

Подставим (6.2) в однородные уравнения Максвелла (3.1.а) получим

Откуда следует, что

(6.3)

Выражение стоящее в круглых скобках (6.3), можно заменить градиентом произвольной скалярной функции , так как ротор градиента равен нулю. Функцию , называют скалярным электродинамическим потенциалом. Таким образом, из (6.3) следует, что

или

(6.4)

Поля E и H, определенные через потенциалы A и  соотношениями (6.2) и (6.4), тождественно удовлетворяют однородным уравнениям Максвелла (3.5). На первый взгляд кажется, что введение электродинамических потенциалов, не дает дополнительных преимуществ для установления связи между полем и током излучения. Однако, на основании неоднородного уравнения Максвелла, можно получить дифференциальные уравнения относительно векторного потенциала А. Для этого, подставим (6.4) в (3.1.б), получим

После преобразования найдем, что

(6.5)

Таким образом, пара уравнений Максвелла (3.1), сводится к одному неоднородному дифференциальному равнению (6.5), но в которое входят произвольные потенциалы  и А. Причина этого заключается во взаимной связи потенциалов А и . Произвольный выбор потенциалов, позволяет установить простую взаимосвязь между ними, положив в (6.5)

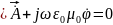
(6.6)

Условия выбора потенциалов в виде соотношения (6.6), называется условием калибровки Лоренца. Калибровка сразу приводит к неоднородному волновому уравнению относительно векторного потенциала А. Из (6.5) получаем

(6.7)

С другой стороны, условие Лоренца, позволяет исключить вектор А из соотношения (6.4), и установить связи между электрическим полем и скалярным потенциалом. Источником поля могут быть динамические заряды с объемной плотностью , поэтому электрическое поле подчиняется уравнению

(6.8)

Из (6.4) и условия Лоренца (6.6) имеем

Объединив полученные соотношения с уравнением (6.8), найдем уравнения относительно скалярного потенциала

(6.9)

Уравнения (6.7) и (6.9) в совокупности с условием Лоренца (6.6), образуют систему уравнений эквивалентных неоднородным уравнениям Максвелла.

Найдем частные решения уравнений (6.7) и (6.9). Для этого воспользуемся результатом решения уравнения Пуассона для статического потенциала  в виде (1.7)

(6.10)

Уравнение для статического векторного потенциала, следует из динамического уравнения (6.7) при k=0

(6.11)

Уравнение Пуассона (1.10) и уравнение (6.11), имеют одинаковую структуру. Поэтому частное решение уравнения (6.11) можно по аналогии с (6.10), представить в виде

(6.12)

В (6.12) интеграл вычисляется по всему пространству определения вектора А, так как r определяется расстоянием между произвольными точками пространства, в котором вычисляется вектор А и точками объема с током .

Теперь рассмотрим условия при которых решения (6.10) и (6.12) уравнений статики, могут быть использованы для динамических уравнений (6.7) и (6.9). Очевидно, что этими решениями можно воспользоваться при очень медленном изменении во времени тока и заряда. Медленным настолько, что время распространения А и  пренебрежимо мало с периодом изменения тока и заряда. При быстрых процессах, когда время распространения полей и период изменения J и  становятся соизмеримыми, необходимо учесть запаздывание потенциалов, заключающееся в том, что поле в точке наблюдения в момент времени t, определяется значениями токов и зарядов в предшествующий момент времени равный ( ), где c – скорость света. Таким образом, переходя к динамическим потенциалам А и  как решениям уравнений (6.7) и (6.9), считаем, что ток и заряд, изменяются по гармоническому закону с учетом запаздывания в виде

Переходя к комплексной форме представления тока и заряда, запишем частные решения динамических уравнений (6.7) и (6.9) в виде

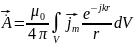
(6.13)

Соотношения (6.13), определяют запаздывающие электродинамические потенциалы в комплексной форме для гармонического поля. Через векторный потенциал А напряженность магнитного поля определяется как . Напряженность электрического поля следует из соотношения (6.4) и условия калибровки (6.6) в виде

(6.14)

Заметим, что в классической электродинамике используют и иные условия, накладываемые на А и , отличные от калибровочного условия Лоренца. Например, можно использовать кулоновскую калибровку, положив . В этом случае из соотношений (6.5) и (6.8), сразу следуют уравнения для потенциалов

Уравнение для  имеет характер квазистатического уравнения Пуассона, что и объясняет название – кулоновская калибровка. Однако, калибровка Лоренца во многих задачах электродинамики предпочтительней, так как она приводит к двум одинаковым уравнениям относительно векторного и скалярного потенциалов.