5.6 Волны te в круглом волноводе

На основание предшествующего анализа волн электрического типа решение уравнения для H_z (5.7.б) можно представить в виде

(5.53)

Налагая граничные условия на стенках волновода получим уравнение для определения поперечного числа

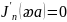
(5.54)

Корни уравнения (5.54) образуют бесконечный дискретный ряд значений корня. Обозначим - произвольный корень из этого ряда. Где m – номер корня. В таблице приведены значения корней для нескольких m и n корней.

Значение критической длины волны для волн магнитного типа могут быть вычислены из соотношения

Основной тип волны с максимальной критической длиной волны отвечает набору индексов m=n=1. В соответствии с таблицей, найдем значение критической волны H₁₁, равное 3.41. Таким образом, волна H₁₁, является основной волной круглого волновода среди электрических и магнитных типов волн. В порядке убывания критической длины волны типы волн волновода типы волн волновода располагаются в ряду. Поля H_0m типа и E_1m типа, имеют одинаковые постоянные распространения. Эти типы полей называются вырожденными.

На основании соотношений (5.17) и (5.53), найдем поперечные составляющие H_mn типа на поперечном сечении волновода

	1	2	3
0	3.83	7.02	10.17
1	7.84	5.33	8.53
2	3.05	6.70	9.97

(5.55)

Полагая в (5.55) m=n=1, запишем составляющие волны H₁₁.

На рис.5.12, показано строение волны H₁₁.

Найдем мощность, передаваемую волной H₁₁ и найдем ее затухание, вызванное омическими потерями. В соответствии с (5.53) и (5.56), передаваемая мощность равна

После интегрирования получим

(5.57)

Интеграл в числителе (5.56) согласно (5.55) равен

Отсюда

Таким образом, коэффициент затухания основной волны круглого волновода H₁₁ равен

(5.58)

Зависимость от частоты представлена на рис.5.11. С ростом частоты затухание стремится к постоянному значению, определяемому соотношением диаметра волновода и длины волны. В диапазоне абсолютное значение волн E₀₁ и H₁₁ близки к значению коэффициента затухания прямоугольного волновода с волной H₁₀ при сравнимых значениях поперечного сечения.

5.7 Электромагнитные поля в резонаторах

Электромагнитные резонаторы (объемные резонаторы), отличаются большим разнообразием форм. Но всех их объединяет одно общее конструктивное свойство – они все представляют собой объемы с замкнутыми металлическими стенками. При этом один из размеров объема, как правило, кратен половине длины волны в волноводе. Цилиндрические объемные резонаторы представляют собой короткозамкнутые отрезки волноводов прямоугольной либо круглой формы. В резонаторах круглой формы Ось z сохраняет свое преимущественное значение перед полярными координатами на поперечном сечении. В круглых цилиндрических резонаторах металлические торцы, расположены нормально к оси z на расстоянии кратном половине длине волны в линии. В прямоугольных резонаторах ориентация системы координат может быть произвольной. В электродинамике электромагнитные поля в резонаторах, рассматриваются как собственные поля, то есть вне связи с окружающим пространством. Собственные поля замкнутого объема могут существовать только на определенных частотах, называемых собственными или резонансными частотами. Далее мы рассмотрим поля в цилиндрических резонаторах с идеально проводящими торцами. Очевидно, что в резонаторах, как отрезках волноводов, могут существовать TE и TM волны, которые в этом случае правильнее называть колебаниями. Поэтому для резонаторов сохраняется представление полей в виде суммы поперечных и продольных составляющих, скалярные двумерные уравнения (5.7) относительно каждой составляющей и соотношение между продольными и поперечными компонентами полей в форе (5.16) и (5.17). Принципиальные отличия резонаторов и волноводов состоит в разных зависимостях полей от координаты z. В волноводах волновой процесс распространяющейся вдоль оси z описывается фазовым множителем . В резонаторах из-за отражения от торцов, устанавливаются стоячие волны или колебания, которым соответствует зависимость в виде . Колебаниям TE или TM типов отвечают разные граничные условия на идеально проводящих торцах, расположенных при z=0 и z=l, где l- длина резонатора. Для TE колебаний, продольная компонента магнитного поля H_z обращается в нуль при z=0 и z=l. Поэтому зависимость H_z от координаты z можно представить соотношением

(5.59)

где - функция поперечных координат, вид которой для TE полей прямоугольного и круглого волноводах получен в предшествующих разделах. Например, из (5.34.а) следует, что

Соотношения (5.6) и (5.16), получены из уравнений Максвелла, в которых производная по z заменена умножением на . Поэтому, применяя (5.16) к резонаторам, надо заменить множитель на производную . Тогда для TE колебаний цилиндрических резонаторов получим

(5.60)

Для TM колебаний на идеально проводящих торцах должна обращаться в ноль поперечная составляющая напряженности электрического поля E, как поля касательного к металлу. Поэтому E=0 при z=0 и z=l. В соотношении (5.17) заменим на производную и представим ее в виде

Таким образом, обращение в ноль на торцах эквивалентно обращению в ноль производной

Следовательно, для TM колебаний резонатора, продольную компоненту электрического поля надо представить в виде

(5.61)

где функция на поперечном сечении координат.

Тогда для TM колебаний цилиндрических резонаторов на основании (5.17) и (5.61) найдем, что

(5.62)

Таким образом, соотношения (5.59) и (5.62), определяют всю совокупность составляющих TE и TM типов собственных колебаний цилиндрических резонаторов.

Найдем в явном виде резонансные частоты и собственные типы колебаний. Вне зависимости от вида поперечного сечения волновода поперечное волновое число и продольное связаны между собой соотношением

(5.63)

В этом соотношении прямоугольного волновода для TE и TM типов полей имеет одинаковые значения, определяемые соотношением (5.34). Для прямоугольных резонаторов (5.63) можно представить в виде, имея в виду, что

Отсюда найдем резонансные частоты и долины волн прямоугольных резонаторов

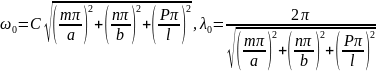
(5.64)

Для круглых цилиндрических волноводов поперечные числа различны для TE и TM типов волн. Ранее они были обозначены для волн TM типа (раздел 5.4) и для волн TE типа (раздел 5.5). Поэтому, резонансные частоты колебаний TM типа круглого цилиндрического резонатора, определяются как

(5.65)

Для колебание TE типа как

(5.66)

Совокупность индексов m, n, p, определяет тип колебания в объемном резонаторе (например H_mnp и E_mnp ) и собственные частоты. Для H_mnp колебаний один из индексов m или n может быть нулем, например, H_m0p, но p0, так как в противном случае поля H типов согласно (5.60) обнуляются. Для колебаний E_mnp типов, индекс p может быть равным нулю. В этом случае поперечное электрическое поле равно нуль соотношение (5.62), а продольная составляющая E_z постоянна. Это означает, что на длине резонатора электрическое поле однородно, и длина резонатора становится неопределенной и может принимать произвольные значения. Заметим, что колебания E_mn0 соответствуют критическому режиму: при p=0 и резонансная частота .

В инженерной практике, размеры резонатора на заданной резонансной частоте, выбираются таким образом, чтобы был обеспечен одномодовый режим резонатора. В этом случае режим резонатора слабо подвержен внешним возмущениям.

Резонаторы на круглых волноводах в отличии от прямоугольных, имеют разные собственные частоты. Колебаниям H₁₁₁ и E₀₁₀, соответствуют низшие собственные частоты, определяемые значениями корней соответствующих уравнений (5.47) и (5.54). Собственная частота H₁₁₁ круглого резонатора в соответствии с (5.65) равна

Собственная частота E₀₁₀, равна

Поэтому в зависимости от отношения длины резонатора к его радиусу, резонансные частоты могут находится в разных соотношениях. Легко найти отношение l/a для случая равных резонансных частот колебаний H₁₁₁ и E₀₁₀. Ранее были приведены значения корней =1.84 и =2.405, поэтому одинаковые резонансные частоты возникают при условии

Отсюда следует, что l/a=2.03. Таким образом при l/a больше чем 2.03 резонансная частота, меньше чем и резонансным колебанием является H₁₁₁. Для “короткого” резонатора l/a меньше чем 2.03, основным резонансным колебанием становится E₀₁₀.