4.2 Электромагнитные волны, распространяющиеся вдоль направления подмагничивания
Рассмотрим распространение плоской однородной волны вдоль направления подмагничивания рис.4.2. Для такой волны в фазовой плоскости (z=const) раздел 3.3. Постоянная распространения волны, очевидно должна быть отлична от постоянной распространения волны в свободном пространстве. Обозначим ее γ. Тогда, возможное решение уравнения Максвелла имеет вид
В этой форме заданы в фазовой плоскости.
Уравнения Максвелла (3.6) для гиротропной среды представим в виде
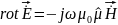
(4.10)
В гиротропной среде, волновой уравнение для H сохранит вид (3.8.а) с тем изменением, что магнитная проницаемость является тензором, определяемым соотношением (4.9). Поэтому волновое уравнение для H примет вид
(4.11)
где
диэлектрическая проницаемость среду.
Допуская решение уравнение (4.11) в виде
плоской однородной волны запишем
и преобразуем (4.11) к виду
(4.12)
Из (4.12) не следует, что выражение стоящее в скобках равно нулю, так как оно является тензором, а тензор не может быть равен нулю. Поэтому, перейдем от (4.12) перейдем к уравнению в проекциях на оси координат. В фазовой плоскости вектор H ориентирован произвольно, поэтому зададим
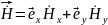
(4.13)
Подставим (4.12) в (4.13) и после преобразований представим (4.12) в проекциях на сои в виде
(4.14)
Как известно, система линейных однородных уравнений тогда и только тогда обладает решениями отличными от нулевого, если определитель системы равен нулю. Приравняем определитель системы (4.14) к нулю, получим
(4.15)
Данное соотношение, является уравнением относительно постоянной распространения γ, так как основные величины в нем известны. Из (4.15) найдем, что
Знак γ определяет только распространения вдоль оси z. Поэтому (4.16) дает два значения γ
(4.16)
Из (4.14) можно получить соотношения между проекциями вектора H. Подставим (4.16) в (4.14) и найдем, что
(4.17)
Таким образом, в феррите вдоль оси намагничивания распространяются две волны с одинаковыми амплитудами и с разными постоянными распространения +γ, и –γ, у которых проекции магнитного поля на оси x и y имеют временной фазовый сдвиг π/2. Как мы знаем (раздел 3.4), суперпозиция этих волн дает две волны с правой и левой круговой поляризацией. Запишем эти волны в виде
(4.18)
В соответствии с (3.9) и (4.18) найдем напряженность электрического поля в волнах правой и левой поляризации
где , равны.
Сложение двух волн с левой и правой круговой поляризацией описывает волну с произвольной поляризацией (3.18). Рассмотрим сумму волн
(4.19)
на произвольном L от начала координат. Положим в (4.16) z=l и подставим в (4.19) и найдем
На основании формулы Эйлера, преобразуем полученное соотношение к виду
(4.20)
Из
(4.20) следует, что положение вектора H
в пространстве будет изменяться: при
l=0 вектор ориентирован
вдоль оси x
, при произвольном l
вектор H будет повернут
относительно оси x на угол
равный. Где определяются из
соотношений (4.20). Подставим в это
соотношение и найдем, что
Подставим
в это соотношение
и
из
(4.20) получим
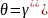(4.21)
На рис.4.3 показан поворот вектора при удалении волны на l от начала координат.
Таким образом, в намагниченном феррите вдоль поля подмагничивания может распространяться плоская однородная волна. При этом происходит вращение плоскости поляризации волны. Это явление как уже упоминалось, называют эффектом Фарадея. Эффект Фарадея в феррите необратим, в том смысле, что поворот плоскости поляризации при обратном распространении волны (в направлении отрицательных направлений z) угол поворота поляризации будет происходить в противоположном направлении из-за изменения знака у .