МИНОБРНАУКИ РОССИИ

Государственное образовательное учреждение высшего профессионального образования

“Санкт-Петербургский государственный электротехнический университет “ЛЭТИ”

им. В.И. Ульянова (Ленина)

И.Г. Мироненко, А.А. Иванов

Электромагнитные поля и волны

Рекомендовано УМО вузов РФ по образованию в области радиотехники, электроники, биомедицинской техники и автоматизации в качестве учебного пособия для студентов, обучающихся по направлению 211000 “Конструирование и технология электронных средств”

Санкт – Петербург

2012 год

Введение

Целью курса является изучение явлений электромагнетизма. Положения лежащие в основе электромагнетизма постоянно развивались и достигли своей вершины с появлением уравнения Максвелла, которые описывали электромагнитные явления во всей их совокупности. Предшествующие Максвеллу исследования электрических и магнитных явлений были связаны с электростатикой и магнитостатикой, то есть с описанием явлений независящих от времени. Изучение Кулоном сил взаимодействия между неподвижных заряженных тел относятся к 1780 – 1785гг. Изучения явлений магнитостатики, начались с работ Эрстеда, который в 1819 году обнаружил, что магнитное поле создается постоянным электрическим током. Проявлением магнитного поля, является сила взаимодействия между токами в проводниках. Впервые Био и Савар (1820г.), а затем Ампер (1825г.), установили основные экспериментальные законы, связывающие магнитные5 поля с токами нашли закон, определяющий силу взаимодействия между токами. Примерно в это же время М. Фарадей (1830г.) пытался установить взаимный характер эффекта Эрстеда, который должен был проявится созданием магнитным полем тока в проводнике. В действительности же Фарадей экспериментально обнаружил появление тока в проводнике при изменение магнитного поля “сцепляющегося” с проводником. Таким оказался результат опытов Фарадея.

Накопленные результаты экспериментальных исследований нужно было отразить в математическом описании, что позволило бы дать единое толкование электрических и магнитных явлений экспериментального закона Фарадея. Это было осуществлено Максвеллом. В 1864 году он опубликовал свою знаменитую работу о динамической теории электромагнитного поля.

Мы начнем изложение теории электромагнетизма с описания постоянных электрических и магнитных полей, в том минимальном объеме, который необходим для обоснования уравнений Максвелла.

Содержание учебного пособия отвечает требованиям федерального государственного образовательного стандарта высшего профессионального образования по направлению 211000 “Конструирование и технология электронных средств”.

ОГЛАВЛЕНИЕ

1.	Электростатические и магнитостатические поля
	1.1	Основные законы электростатики
	1.2	Основные сведения из магнитостатики
2.	Переменные во времени поля
	2.1	Закон электромагнитной индукции Фарадея
	2.2	Максвелловский ток смещения. Уравнения Максвелла
	2.3	Энергия электромагнитного поля. Теорема Пойнтинга
	2.4	Граничные условия для электромагнитного поля
3.	Гармонические плоские волны
	3.1	Уравнения Максвелла для гармонических полей
	3.2	Вектор Пойнтинга для гармонических полей
	3.3	Волновые уравнения для гармонических полей. Плоские волны
	3.4	Круговая поляризация плоских волн
	3.5	Затухание плоских волн в среде с потерями
	3.6	Суперпозиция плоских волн с близкими частотами. Групповая скорость
	3.7	Отражение и преломление плоских волн на плоской границе раздела сред
	3.8	Полное отражение от диэлектрической границы
4.	Электромагнитные волны в гиротропной среде
	4.1	Тензор магнитной проницаемости намагниченного феррита
	4.2	Электромагнитные волны в продольно намагниченном феррите
	4.3	Электромагнитные волны в поперечно намагниченном феррите
5.	Электромагнитные волны в направляющих структурах
	5.1	Общие свойства электромагнитных волн в направляющих структурах
	5.2	Поток мощности и затухание в волноводах
	5.3	Волны TE в прямоугольном волноводе
	5.4	Волны TM в прямоугольном волноводе
	5.5	Волны TM в круглом волноводе
	5.6	Волны TE в круглом волноводе
	5.7	Электромагнитные колебания в резонаторах
	5.8	Добротность резонаторов
	5.9	Диэлектрические волноводы
	5.10	Коаксиальные волноводы
6.	Излучение и дифракция электромагнитных волн
	6.1	Электродинамические потенциалы
	6.2	Излучение электрического диполя
	6.3	Поле в дальней зоне линейной антенны
	6.4	Излучение магнитного диполя
	6.5	Дифракция плоской волны на круглом металлическом цилиндре
	6.6	Дифракция плоской волны на круглом диэлектрическом цилиндре
	6.7	Дифракция на отверстии в проводящем экране
	6.8	Дифракция на круглом отверстии в проводящем экране
7.	Приложение

1. Электростатические и магнитостатические поля

1.1. Основные сведения из электростатики

Всю совокупность электростатических явлений описывают несколько экспериментальных законов, из которых первый – закон Кулона. Кулон установил, что сила взаимодействия двух небольших заряженных тел, расстояние между которыми велико по сравнению с их размерами, пропорциональна величине каждого заряда, обратно пропорциональна квадрату расстояний между ними, и направленной вдоль прямой, соединяющей заряды. В пустоте эта сила равна

, (1.1)

где r – расстояние между телами, q, q^’ – заряды тел, - орт направления силы.

В системе МКС заряд определяется в кулонах ₀ – диэлектрическая проницаемость вакуума ₀ = 8.85610^-12 Ф/м.

Соотношение (1.1) можно представить в ином виде, введя скалярную величину

(1.2)

Её называют потенциалом, создаваемым зарядом q^’ в месте расположения заряда q. Эквивалентная форма записи соотношения (1.1) через потенциал (1.2) имеет вид

(1.2^*)

Поэтому через (1.2) соотношение (1.2^*) приводит к (1.1).

Сила F направлена по оси расположения тел и противоположна направлению градиента потенциала.

Экспериментально было установлено, что совокупность малых заряженных тел действует на какое либо малое заряженное тело с силой равной векторной сумме сил Кулона каждого заряда и совокупности. Это является условием линейной суперпозиции в электростатике. Рассмотрим с формальной стороны это утверждение. Пусть n заряженных тел q₁, q₂, .. q_n взаимодействуют с телом имеющим заряд q. Векторную сумму сил действующих на заряд q запишем в соответствии с принципом суперпозиции в виде

(1.3)

где r_i (i=1,2..n) – расстояния между i- тым зарядом и зарядом q, - орты направлений между i- ым и зарядом q. Согласно (1.2) и (1.2^*) соотношение (1.3) можно представить в виде

(1.4)

где

На основании правил вычисления градиента запишем соотношение (1.4) в виде

(1.5)

где

В экспериментах Кулона измеряемой величиной является сила. Но оказалось, что целесообразно ввести понятие напряженности электрического поля, обусловленного совокупностью заряженных тел. Напряженность электрического поля называют силу действующую на единичный заряд. При таком определении, напряженность электрического поля в соответствии с (1.5) равна

(1.6)

и, соответственно, сила действующая на заряд q равна . Величины и вычисляются в месте расположения заряда q, но не включают потенциал создаваемым этим зарядом.

При непрерывном распределении заряда в объеме V – с объемной плотностью , каждый заряд q_i в соотношениях (1.3) - (1.5) можно заменить на где элемент объема. Для этого случая в соотношении (1.5)следует перейти от суммы к интегралу. Тогда потенциал созданный непрерывным распределением заряда в произвольной точке пространства вычисляется как

, (1.7)

где r расстояние между произвольными точками объема и точками пространства. Поэтому интегрирование производится по всему бесконечному пространству, в котором определяется .

Таким образом, подводя краткий итог, можно сказать, что распределение зарядов создает силовое поле характеризуемое напряженностью вы каждой точке пространства. В соответствии с математической теорией поля вектор напряженности E направлен по касательной к силовой линии поля.

Интегральное соотношение для потенциала (1.7) дает возможность определения напряженности электрического поля с помощью соотношения (1.6). Существует другое интегральное соотношение, называемое теоремой Гаусса, на основании которого можно получить дифференциальное уравнение для потенциала поля.

Сформулируем теорему Гаусса для одиночного заряда q. Окружим заряд сферической поверхностью радиуса r с центром в месте расположения заряда. В соответствии со сферической симметрией, силовые линии поля и вектор напряженности E совпадают и направлены по радиусу сферы. Следовательно, поток напряженности через поверхность сферы равен

где ds – элемент поверхности. На поверхности сферы в соответствии с (1.2) и (1.6^*) напряженность поля равна

поэтому очевидно, что поток .

Таким образом, теорему Гаусса для рассмотренного частного случая можно сформулировать следующим образом: поток вектора E через сферическую поверхность окружающую заряд q, пропорционален заряду. Этот вывод можно обобщить на произвольную поверхность и на непрерывное распределение заряда внутри ее с объемной плотностью . Запишем теорему Гаусса для общего случая в виде

. (1.8)

От интегральной формы теоремы Гаусса перейдем к дифференциальной. Для этого, на основании формулы Грина левую часть (1.8) преобразуем к виду

.

В этом соотношении V – объем ограниченный поверхностью S. Следовательно (1.8) можно преобразовать к виду

.

Отсюда следует, что

(1.9)

Подставим в (1.9) вместо Е соотношение (1.6) и найдем, что

(1.10)

где

Соотношение (1.10) называется уравнением Пуассона, решением которого является распределение потенциала создаваемое зарядом . Потенциал вне объема, занятого зарядом, является решением уравнения Лапласа

(1.11)

Решением уравнения Пуассона, является соотношение (1.7) так как для иного утверждения нет основания.

Соотношения, полученные выше, относятся к свободному пространству (вакууму). Опыты Фарадея показали, что внесение диэлектрика в пространство между электродами конденсатора приводит к уменьшению разности потенциалов между ними. Это дает основание к выводу, что диэлектрик увеличивает емкость конденсатора. Отношение значений емкости идеального (без краевого эффекта) конденсатора с диэлектриком и без него, называют относительной диэлектрической проницаемостью , всегда больше единицы. Абсолютная диэлектрическая проницаемость диэлектрика равна . Поэтому доля диэлектрической среды надо видоизменить теорему Гаусса, заменив в (1.8) вектор напряженности поля Е на новый вектор D и записать условие сохранения потока поля в диэлектрической среде в виде

Отсюда на основании теоремы Стокса следует, что

и следовательно

(1.12)

Поскольку напряженность поля создаваемая зарядом  в диэлектрической среде в  раз слабее чем в свободном пространстве, то в соответствии с соотношение (1.9) вектор D связан с напряженностью Е соотношением

(1.13)

Вектор D называют вектором электрической индукции. Максвелл назвал его электрическим смещением, считая, что под действием электрического поля в диэлектрике частицы смещаются в пределах упругости пропорционально действующей силе, то есть напряженности поля Е. Таким образом, описание электростатического поля в диэлектрике неизбежно связано с моделью вещества, при обосновании которой приходится делать упрощающие предположения. Одним из них, является представление о диэлектрике как о совокупности неподвижных связанных между собой положительных и отрицательных зарядов, эквивалентных заряду электронного облака и заряду “остова” молекулы. В этой модели, молекулу можно рассматривать как эквивалентный диполь, образованный двумя равными зарядами q с противоположными знакам, расположенными на расстоянии d. Значение d имеет порядок размера молекулы. Если в объеме V находится N атомов, то можно ввести дипольный момент единицы объема P, который равен

В среднем диэлектрик электрически нейтрален. Но в электрическом поле положительные и отрицательные заряды образующие диполь смещаются в противоположных направлениях. Таким образом в электрическом поле возникает поляризация вещества: диполи выстраиваются вдоль силовых линий поля и в диэлектрике возникают связанные заряды, объемную плотность которых обозначим _св. Дипольный электрический момент в пределах упругого взаимодействия поля и вещества пропорционален напряженности внешнего электрического поля. Поэтому

и соотношения для P представим в виде

(1.14)

где - поляризуемость вещества.

Дипольный электрический момент единицы объема называют вектором поляризации вещества.

На основании теоремы Гаусса можно утверждать, что поток вектора поляризации будет равен связанному заряду. По аналогии с (1.8) запишем

(1.15)

Применяя теорему Стокса получим дифференциальное соотношение для , аналогичное (1.12)

(1.16)

Таким образом, если в диэлектрике имеются свободные заряды  не связанные с поляризацией, то уравнение (1.9) следует переписать с учетом плотности полного заряда в виде

С учетом (1.16) имеем

Значит

(1.17)

Сравнение соотношений (1.12) и (1.17) приводит к выводу, что

(1.18)

Откуда с учетом (1.14) и (1.13) следует, что относительная диэлектрическая проницаемость вещества и его поляризуемость связаны соотношением

(1.19)

Соотношение (1.18) справедливо всегда, однако линейные соотношения для индукции поляризации и напряженности поля сохраняются при условии их малых значений.

1.3 Основные сведения из магнитостатики

Магнитные явления существенно отличаются от электрических. Это объясняется рядом причин, среди которых наиболее важная – отличие в природе магнитных зарядов. В магнитных исследованиях основным объектом является магнитный диполь, простейшей реализацией которого является магнитная стрелка. Статические магнитные поля возникают вокруг проводников, по которым течет постоянный электрический ток. Вблизи проводников с током магнитный диполь ориентируется в определенном направлении, которым считается направление плотности магнитного потока или магнитной индукции .

Описание магнитных явлений состоит в установлении связей между током и магнитным полем. Основное соотношение, которое было получено Био и Саваром, можно сформулировать следующим образом. Пусть D ориентированный элемент длины бесконечно тонкого провода, несущего ток I, r – радиус вектор, проведенный в точку наблюдения от элемента dl рис.1.1. Согласно теореме Био – Савара – Лапласа, величина магнитной индукции , создаваемой элементом dl в точке наблюдения определяется соотношением

(1.20)

где 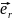- орт радиуса вектора, ₀ магнитная проницаемость вакуума ₀=410^-7 Гн/м. Интегрируя (1.20) найдем, что

(1.21)

Отсутствие магнитных зарядов, приводит к тому, что силовые линии магнитного поля всегда замкнуты. Поэтому любая замкнутая поверхность, выделенная в магнитном поле, но не охватывающая провод с током, пересекается с силовыми линиями магнитного поля четное число раз. Следовательно, поток магнитной индукции через такую поверхность равен нулю

(1.22)

На основании формулы Стокса из (1.22) следует, что

(1.23)

По аналогии с электростатическим полем напряженность магнитного поля H можно определить как

Величина  - называется относительной магнитной проницаемостью среды, а H, является предельным значением индукции в вакууме, для которого =1.

Вернемся к соотношению (1.21) и преобразуем его для прямолинейного провода конечного поперечного сечения. Направим ось провода вдоль оси z, выделим элементарный объем провода dV, отстоящий от z=0 на удалении равном z. Вдоль провода течет электрический ток, плотность которого

Выделенный элемент с током создает в точке P магнитное поле напряженностью . Ток в проводнике есть поток вектора плотности тока через поперечное сечение провода, поэтому

В большинстве случаев не учитывается возможная неравномерность его плотности на поперечном сечении, поэтому . С учетом сказанного представим (1.20) для элемента прямолинейного провода в виде

Результирующую напряженность магнитного поля в точке P найдем проинтегрировав dH по всей длине провода

В этом соотношении векторное произведение

Поэтому напряженность магнитного поля линейного тока в произвольной точке пространства вне провода определяется соотношением

Интеграл имеет точное значение равное

Следовательно

(1.23)

Силовые линии поля образуют окружности вокруг провода. Найдем циркуляции напряженности магнитного поля по силовой линии полагая, что dL как элемент окружности равен . Поэтому

Полученное соотношение представляет закон Ампера в интегральной форме. Он получен для прямолинейного провода, но может быть распространен и на общий случай: циркуляция магнитного по контуру, охватывающему ток равна значению тока в контуре

(1.24)

От интегральной формы закона Ампера, перейдем к дифференциальной. Перепишем (1.24) в виде

И на основании теоремы Стокса найдем, что

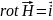
(1.25)

Соотношение (1.25) выражает закон Ампера в дифференциальной форме. Он играет такую же роль в электростатике как и закон Гаусса в электростатике.

Подведем краткий итог предыдущих разделов. В электростатике напряженность электрического поля может быть вычислена из закона Кулона, но такому методу расчета противостоит расчет поля через дифференциальное уравнение Лапласа или Пуассона. Это соответствует замене интегральных соотношений на дифференциальные уравнения в частных производных. Так же обстоит дело и в магнитостатике. Но несмотря на аналогию между электро и магнитостатикой надо иметь ввиду, что она неполная. Например, напряженность магнитного поля H как и электрическая индукция D не являются первичными величинами. Основными величинами в микроскопической теории являются напряженность электрического поля Е и магнитная индукция B, которую и следует считать истинным аналогом напряженности электрического поля. Кроме того, аналогия пропадает при введении магнитного скалярного потенциала, через соотношение B= , что очевидно следует из уравнения rotH=0.

Магнитный скалярный потенциал обладает близкими математическими свойствами к электростатическому потенциалу, но как показано в магнитостатике он многозначен. При пересечении поверхности ограниченной контуром с током, потенциал претерпевает разрыв на величину тока. Таким образом B нельзя выразить через скалярный магнитный потенциал при исследовании полей в области токов.

2. Переменные во времени поля

2.1 Закон индукции Фарадея.

Явление электростатики и магнитостатики существуют независимо друг от друга. Единственным связующим звеном этих явлений является то обстоятельство, что стационарные токи, порождающие магнитные поля, создаются движущимися зарядами. В переменных во времени полях, независимость электрических и магнитных явлений исчезает: при изменении магнитного поля, появляется электрическое поле, а изменение электрического поля, порождает переменное магнитное поле. Таким образом, переменные магнитные поля, образуют новое явление – электромагнитное поле. Другими словами, электромагнитное поле представляет собой самосогласованный процесс, в котором переменные электрическое и магнитное поля существуют одновременно как единое целое.

Изучение электромагнитного поля как фактически существующего явления и установление первых количественных соотношений, описывающих взаимосвязь переменных электрических и магнитных полей, принадлежит М. Фарадею (1831г.). Фарадей создавал переменное магнитное поле включением и выключением тока в контуре, и перемещением контура в поле постоянного магнита. Он установил факт появления тока в связанном с полем в контуре и в контуре пересекающем поле постоянного магнита. Фарадей интерпретировал эти экспериментально наблюдаемые явления, как следствие изменения магнитного потока пронизывающего контур. По Фарадею, изменение магнитного потока индуцирует в контуре электрическое поле, линейный интеграл от которого по контуру, есть электро движущая сила (ЭДС). Под действием ЭДС в замкнутом контуре течет ток, значение которого определяется законом Ома.

Максвелл ввел поток магнитной индукции

(2.1)

где S –поверхность ограниченная контуром, B – вектор магнитной индукции пронизывающий контур рис.2.1. Изменение потока магнитной индукции, введенной Максвеллом, объединяет все причины, приводящие к индуцированию электрического поля в проводящем контуре, который исследовал Фарадей.

Электродвижущая сила в контуре определяется как линейный интеграл от напряженности электрического поля

(2.2)

где Е – напряженность электрического поля на элементе dl контура L.

Наблюдения Фарадея, Максвелл представил в математической форме в виде

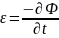
(2.3)

По Максвеллу ЭДС пропорциональна скорости изменения потока пронизывающего контур. Коэффициент K выбирается из системы единиц в которой определяется поток и ЭДС. В МКС коэффициент К=1. Обратим внимание на то, что наблюдения Фарадея и количественные соотношения (2.1) – (2.3) относятся к проводящим замкнутым контурам.