Физическая интерпретация

Пусть движение несжимаемой жидкости единичной плотности в пространстве задано векторным полем скорости течения . Тогда масса жидкости, которая протечёт за единицу времени через поверхность S будет равна потоку векторного поля через поверхность S.

2.4. Ротор (вихрь) векторного поля.

Определение. Ротором векторного поля называется вектор, записанный в виде:

.

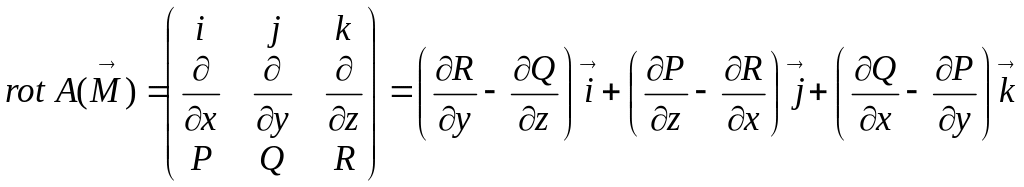Основные свойстваротора:

1. , - произвольные постоянные.

2. .

3.

Показывает, насколько и в каком направлении закручено поле в каждой точке.

Векторное поле, ротор которого равен нулю в любой точке, называется потенциальным (безвихревым).

2.5. Циркуляция

Термин «циркуляция» был первоначально введен в гидродинамике для расчета циркуляции жидкости по замкнутому каналу. Рассмотрим течение идеальной несжимаемой жидкости. Выберем произвольный контур Γ. Мысленно представим, что мы заморозили всю жидкость в объеме, за исключением тонкого канала, включающего в себя контур Γ. Тогда, в зависимости от первоначального характера течения жидкости, она будет либо неподвижной в канале, либо двигаться вдоль контура (циркулировать). В качестве характеристики такого движения берут величину равную произведению скорости движения жидкости по каналу v' на длину контура l. C = v'l

Так как при затвердевании стенок канала нормальная к контуру компонента скорости будет погашена, жидкость по каналу будет двигаться с тангенциальной составляющей исходной скорости v_τ. Тогда циркуляцию можно представить в виде

где dl — элемент длины контура.

Определение. Циркуляцией векторного поля называется криволинейный интеграл второго рода, взятый по произвольному замкнутому контуру Γ. По определению , где — векторное поле (или вектор-функция), определенное в некоторой области D, содержащей в себе контур Γ, — бесконечно малое приращение радиус-вектора . Окружность на символе интеграла подчёркивает тот факт, что интегрирование производится по замкнутому контуру.

Свойства циркуляции

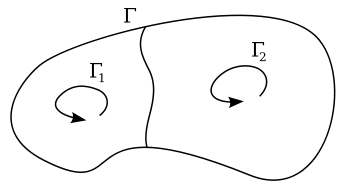
Свойство аддитивности циркуляции: циркуляция по контуру Γ есть сумма циркуляций по контурам Γ₁ и Γ₂, то есть C = C₁ + C₂

Формула Стокса

Циркуляция вектора А по произвольному контуру Г равна потоку вектора через произвольную поверхность S, ограниченную данным контуром.

 — Ротор (вихрь) вектора F.

В случае, если контур плоский, например лежит в плоскости OXY, справедлива формула Грина

,где int Г— плоскость, ограничиваемая контуром

где i, j и k — единичные орты для осей x, y и z соответственно.

Пример 5. Найти циркуляцию вектора по окружности в положительном направлении.

Решение: Циркуляция вектора равна

>> syms t a

>> int(a^2*sin(t)^2+a^2*cos(t)^2,t,0,2*pi)

ans = 2*a^2*pi

3. Оператор Гамильтона и векторные дифференциальные операции второго порядка.

Оператор Гамильтона (Оператор набла) - это векторный дифференциальный оператор, который в декартовых координатах определяется формулой:

Сам вектор не имеет реального значения, он приобретает определённый смысл лишь в комбинации со скалярными или векторными функциями.

Представим grad, div и rot через оператор набла:

1. Произведение вектора на скалярную функцию даёт градиент этой функции

.

2. Скалярное произведение вектора на векторную функцию даёт дивергенцию этой функции

.

3. Векторное произведение вектора на векторную функцию даёт ротор этой функции

.

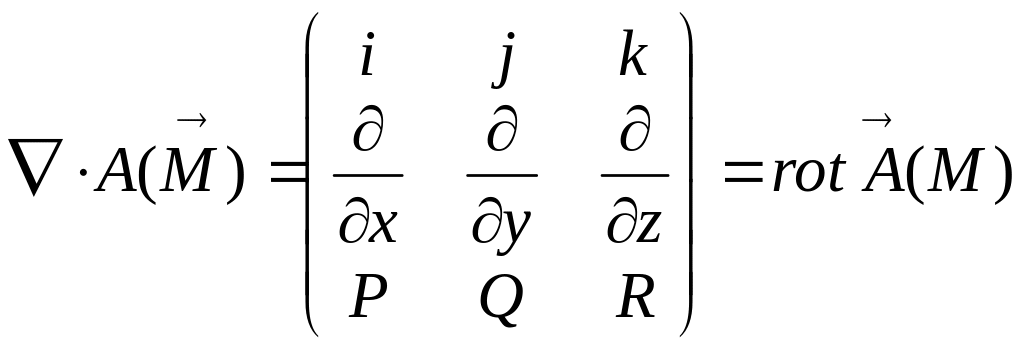Действия взятия градиента, дивергенции, ротора называются векторными дифференциальными операциями первого порядка, т.к. в них участвуют только первые производные.

В приложениях встречаются векторные дифференциальные операции второго порядка.

Оператор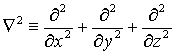 называется оператор Лапласа в декартовых координатах.

Дифференциальные операторы второго порядка: