Графики поля градиентов quiver

Для построения графиков полей градиента служат команды quiver:

• quiver(X.Y.U.V) — строит график поля градиентов в виде стрелок для каждой пары элементов массивов X и Y, причем элементы массивов U и V указывают направление и размер стрелок;

• qui ver(U, V) — строит векторы скорости в равнорасположенных точках на плоскости (х, у);

• quiver(U,V,S) или quiver(X,Y.U,V,S) — автоматически масштабирует стрелки по сетке и затем вытягивает их по значению S. Используйте S=0, чтобы построить стрелки без автоматического масштабирования;

• quiver(...,LINESPEC) — использует для векторов указанный тип линии. Указанные в LINESPEC маркеры рисуются у оснований, а не на концах векторов. Для отмены любого вида маркера используйте спецификацию '.'. Спецификации линий, цветов и маркеров были подробно описаны в разделе, посвященном команде plot;

• H=quiver(...) — строит график и возвращает вектор дескрипторов. Ниже представлен пример применения команды quiver:

Пример 3: Рассмотрим расчет и построение поля направлений для функции F = с использованием функции gradient.

>>[x, y] = meshgrid(-2:.2:2, -2:.2:2);

>>z = x .* exp(-x.^2 - y.^2); >>[px, py] = gradient(z, .2, .2); >>contour(z), hold on, quiver(px, py), hold off

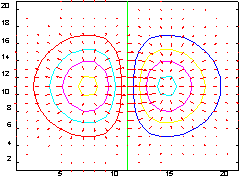
Нетрудно заметить, что представление поля градиентов стрелками дает весьма наглядное представление о 'линиях поля, указывая области, куда эти линии впадают и откуда они исходят.

2. Векторное поле.

Определение: векторным полем называется часть пространства (или всё пространство), в каждой точке которого задана некоторая векторная величина , где - проекции вектора на оси координат, которые зависят от координат точки М(х,у,z). Т.о. задание векторного поля равносильно заданию трёх скалярных полей – проекций векторного поля на направление единичных векторов .

Конкретными физическими примерами векторных полей являются: поле скоростей текущей жидкости, силовые поля (поле тяготения, электрическое и электромагнитное поля).

2.1 Векторные линии.

Определение. Векторной линией векторного поля называется линия, в каждой точке которой касательная совпадает с вектором соответствующим этой точке.

Чтобы изучить определённое векторное поле, изучают расположение векторных линий.

- это система дифференциальных уравнений семейства векторных линий поля .

2.2 Дивергенция (расходимость) векторного поля

Определение. Дивергенцией векторного поля в точке называется скаляр вида .

Основные свойства дивергенции:

1. , - произвольные постоянные.

2. .

3.

Физический смысл:

2.3. Поток вектора.

Пусть векторное поле образовано вектором .

Возьмём в этом поле некоторую двухстороннюю поверхность S и выберем на ней определённую сторону, указав направление нормали к поверхности.

Определение. Потоком (К) вектора через поверхность S называется интеграл по поверхности (S) от скалярного произведения вектора поля на единичный вектор нормали ( ) к поверхности, т.е.

Т.к. , то формулу можно записать

или .

Если S – внешняя сторона замкнутой поверхности , ограничивающей объём V то для вычисления потока можно использовать формулу Остроградского .