Лекция №18 Элементы теории поля

1. Скалярное поле.

Определение. Полем называется часть пространства (или всё пространство), в каждой точке которого поставлено в соответствие определённое значение физической величины «И».

Поле называется скалярным, если «И» скалярная величина. Если выбрана некоторая декартова система координат, то задание скалярного поля эквивалентно заданию функции трёх переменных в пространстве или заданию функции двух переменных на плоскости; в этом случае поле называется плоским полем. Примеры физических полей: поле температур, поле электрического потенциала, поле тяготения масс.

1.2. Поверхности уровня, линии уровня

Множество всех точек М из области V , в которых выполняется равенство , где С – некоторая постоянная, называется поверхностью уровня, соответствующей числу С. Семейство поверхностей уровня скалярного поля в декартовых координатах определяется уравнением , где С - произвольное действительное число.

Замечание: для плоского поля уравнение определяет линии уровня.

Для построения линий уровня соответствующих поверхностей в среде Matlab используются функции contour:

contour(X,Y,Z) – строит линии уровня для поверхности Z =Z(X,Y),

contour(X,Y,Z,n) - то же с указанием числа линий уровня (по умолчанию 10),

contour(X,Y,Z,v) - то же для массива указанных значений ;

contour(Z), contour(Z,n), contour(Z,v) - аналогичные функции без указания диапазонов для аргументов

contour(...,LineSpec) - аналогичные функции c указанием типа и цвета линий (см. plot); [C,h]=contour (...) возвращает массив С и вектор дескрипторов, позволяя тем самым продолжить работу с рисунком (давать оцифровку линий, заголовки и др.).

Функция contourf(...) закрашивает области между линиями уровня, аналогична contour(...) с разницей в формате[C,h, cf]=contour (...), где cf определяет матрицу раскраски.

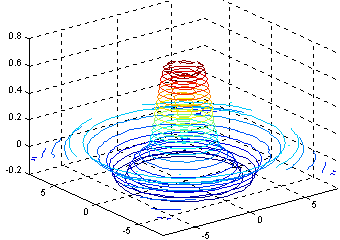
Функция contour3(...) по синтаксису полностью аналогична contour(...),изображает линии уровня в пространственной интерпретации; так команда [c,h]=contour3(x,y,z,20); дает фигуру (рис.3).

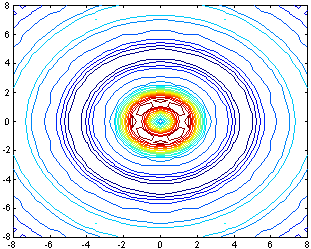
Пример 1: построить линии уровня заданной поверхности

>> [x,y]=meshgrid(-8:0.5:8); >> t=sqrt(x.^2+y.^2)+0.001; >> z=sin(t).^3./t; >> [c,h]=contour(x,y,z,20);	>> [x,y]=meshgrid(-2:0.25:2); >> t=sqrt(x.^2+y.^2)+0.001; >> z=sin(t).^3./t; >> [c,h,cf]=contourf(x,y,z,4);
Рис.1	Рис.2	Рис.3

Для маркировки контурных графиков используются команды группы clabel:

• сlabel(CS, H) – маркирует контурный график с данными в контурной матрице CS и дескрипторами объектов, заданными в массиве Н. Метки вставляются в разрывы контурных линий и ориентируются в соответствии с направлением линий;

• сlabel(CS, H, V) – маркирует только те уровни, которые указаны в векторе V. По умолчанию маркируются все контуры. Позиции меток располагаются случайным образом;

• сlabel(CS, H, ‘manual’) – маркирует контурные графики с установкой положения маркеров с помощью мыши. Нажатие клавиши Enter или кнопки мыши завершает установку маркера. При отсутствии мыши для перехода от одной линии уровня к другой используется клавиша пробела, а для перемещении надписи используются клавиши перемещения курсора;

• сlabel(CS), сlabel(CS, V), сlabel(CS, H, ‘manual’) – дополнительные возможности маркировки контурных графиков.

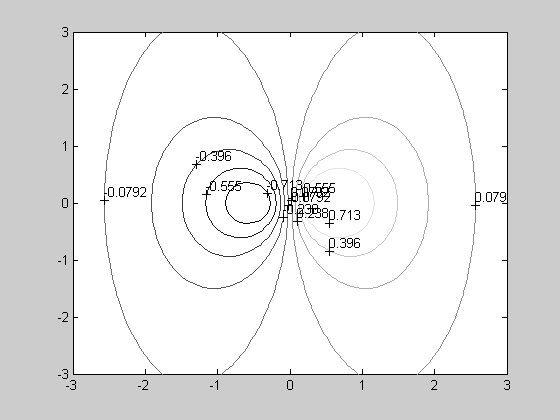
Пример использования функции сlabel

>> [X,Y]=meshgrid([-3:0.1:3]); >> Z=sin(X)./(X.^2+Y.^2+0.3;) >> Z=sin(X)./(X.^2+Y.^2+0.3); >> C=contour(X,Y,Z,10); >> colormap(gray) >> clabel(C)