Вступ

Початок розвитку теорії ймовірностей і математичної статистики пов'язаний з європейськими математиками XVII століття. Завдяки роботам швейцарського математика Якоба Бернуллі теорія ймовірностей набула важливого значення в практичній діяльності. Він побудував математичну модель для опису серії незалежних випробувань, довів теорему, яка є частковим випадком закону великих чисел (теорему Бернуллі), що має основне значення в теорії ймовірностей і її застосування до математичної статистики. В XVIII столітті англійський математик Томас Байес поставив і вирішив одну з основних задач елементарної теорії ймовірностей - теорему гіпотез, відому за назвою «формула Бейєса».

В XIX столітті теорія ймовірностей сформувалась як злагоджена математична дисципліна в завдяки видатним роботам російського математика П.Л. Чебишева і його учнів Ляпунова О.М. і Маркова А.А. Чебишев П.Л. довів загальні форми закону великих чисел. Марков Андрій Андрійович збагатив теорію ймовірностей важливими відкриттями й методами. Він розвив метод моментів Чебишева настільки, що став можливим доказ центральної граничної теореми; істотно розширив сферу застосування закону великих чисел і центральної граничної теореми, поширивши їх не тільки на незалежні, але й на залежні досліди; заклав основи однієї із загальних схем природних процесів, що згодом назвали ланцюгами Маркова. Це привело до розвитку нового розділу теорії ймовірностей - теорії випадкових процесів. У математичній статистиці А.А.Марков вивів принцип, еквівалентний поняттям незміщених і ефективних статистик. Наукова і практична діяльність Ляпунова Олександра Михайловича пов’язана з роботою у Харківському університеті. Він зробив важливий внесок у теорію ймовірностей, давши простий і строгий доказ центральної граничної теореми в більш загальній формі порівнюючи з підходами Чебишева і Маркова. З цією метою для доведення він розробив метод характеристичних функцій, що широко застосовується в сучасній теорії ймовірностей.

Застосування імовірнісних і статистичних методів дає можливість вивчати на науковій основі як діяльність окремих підприємств, так і соціально-економічні процеси в суспільстві в цілому.

1 Статистичне дослідження залежностей

При дослідженні систем випадкових величин варто розглянути питання про їх взаємозалежність або незалежність. Зокрема, залежність однієї випадкової величини від значень іншої називають кореляційною.

Якщо випадкові величини X і Y лише стохастично залежні, то виникає завдання наближеного подання Y ≈ f(X) однієї величини через іншу. Самим зручним і загальноприйнятним є наближення по методу найменших квадратів.

Величина f (X) називається найкращим (у сенсі методу найменших квадратів) наближенням для Y , якщо 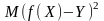набуває найменш можливе значення. У цьому випадку величина f (X) − середня квадратична регресія Y на X .

Якщо параметри регресії визначають за результатами спостережень, регресію називають емпіричною, або вибіркової. Дані спостережень у випадку системи двох випадкових величин X і Y записують у вигляді кореляційної таблиці 1.1.В даній курсовій роботі

Таблиця 1.1 – Кореляційна таблиця.

		Х
	Х Y			…
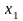
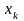
Y				…
				…
	…	…	…	…	…	…
				…
				…

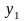
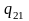
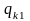
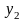
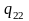
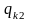
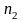
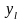
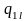
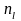
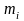
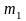
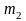
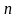
де m_i − число спостережень X = x_i , n_i − число спостережень Y = y_i ,

q_ij−число спостережень пари (x_i; y_i), .

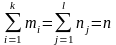Доведено, що рівняння лінійної регресії можна записати у вигляді:

y=Ax+B, (1.1)

де A = rσ(Y)/σX; . Найбільш популярною оцінкою наближення Y лінійною регресією є емпіричний коефіцієнт кореляції, який обчислюється за формулою:

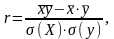(1.2)

де величина 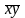має назву змішаного середнього і обчислюється за формулою:

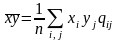(1.3)

ЗАДАЧА 1

Результати дослідження залежності об’єму досліджуваного газу Y від температури X для 166 рівноточних вимірювань наведені кореляційній таблиці

		Х
	(X,Y)	10	17	24	31	38	45
Y	16	6	7					13
	22		13	19	11			43
	28			29	44			73
	34				20	8	9	37
		6	20	48	75	8	9	166

Потрібно:

1) побудувати емпіричну ламану регресії Y на X ;

2) вибрати вид рівняння регресії;

3) оцінити залежність між Y і X емпіричним коефіцієнтом кореляції;

4) скласти емпіричне рівнянні регресії;

5) накреслити графік лінії регресії (у системі координат,

використовуваної для побудови емпіричної ламаної).

Розв’язок: 1) Для побудови емпіричної ламаної регресії Y на X обчислимо середнє значення об’єму досліджуваного газу при кожному значенні температури:

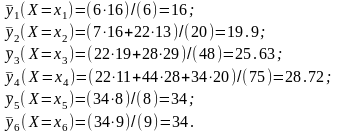
Потім наносимо точки на площину в системі координат XОY і з'єднуємо їх відрізками прямих (рис.1).

2) Розташування точок на площині ХОY дозволяє припустити наявність прямолінійної кореляційної залежності між Y і X .

3) Обчислюємо коефіцієнт кореляції і параметри рівняння регресії:

Порівняно невелике значення r , яке за позначенням r [-1,1], підтверджує припущення про лінійну кореляційну залежність між Y і X .

4) Емпіричне рівняння регресії має вигляд: y= 0.55x+11.8 .

5) Накреслимо графік лінії регресії (рис.1).

Взаємне розташування на рисунку емпіричної ламаної і емпіричної прямої регресії свідчить про те, що припущення про лінійну регресію згідно з результатами спостережень.

Аналітично це питання вирішується за допомогою перевірки гіпотези про значимість коефіцієнта кореляції.

Висновок: кореляційний зв‘язок прямий і тісний.