3.4. Выбор и расчет технических средств сау

Горение соответствует процессу окисления — соединению кислорода с горючими элементами топлива, происходящему с большой скоростью с выделением тепла и света. Для возникновения горения необходимо, чтобы реагирующие вещества — горючее и кислород — были доведены до температуры воспламенения, т. е. до температуры, при которой может происходить реакция горения

При расчете горения топлива определяют количество расходуемого при сжигании воздуха, количество и состав образующихся продуктов горения. Эти расчеты могут быть выполнены по данным элементарного состава топлива на основе уравнений горения. При этом, по предложению французского ученого Дюлонга, считают, что весь кислород, находящийся в топливе, соединен с водородом. Поэтому количество водорода, находящегося в топливе, при определении потребного количества кислорода

уменьшают на величину.

В связи с тем что расчет горения топлива по элементарному составу трудоемок и зачастую при производстве теплотехнических расчетов отсутствует полный анализ его, для технических расчетов обычно пользуются формулами приближенного расчета горения

4. Расчёт и анализ системы автоматического управления параметром

4.1. Математическое описание объекта управления

С целью получения модели исследуемого объекта управления, с дальнейшим ее использованием при синтезе системы управления, а также при ее расчете, был использован активный экспериментальный метод моделирования. То есть на вход исследуемого объекта подавались сигналы определенного вида (ступенчатые воздействия), и фиксировались изменения выходных переменных. Также была проведена аппроксимация экспериментальных кривых, и были получены следующие модели объектов.

Берем за основу разгонную характеристику котла Buderus Logano S825, как объекта регулирования температуры воды на выходе из котла при управляющем воздействии – увеличение подачи топлива.

1. Модель объекта по каналу управления (контур температуры котловой воды): зависимость температуры воды от расхода газа.

Изменение расхода газа:

Параметры входного воздействия (расход газа):

значение входного воздействия до эксперимента = 0 м³ /час

значение входного воздействия после эксперимента = 151,29 м³ /час.

Экспериментальная кривая температуры воды представлена на рис.3.1.1.

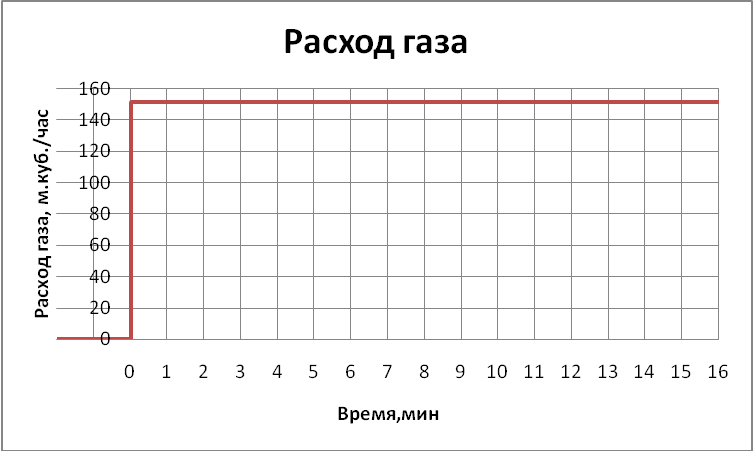
Рис.3.1.1.

Параметры выходного сигнала объекта (температура воды):

среднее значение выходного сигнала до опыта = 56,5 ºС

установившееся среднее значение выходного сигнала после

эксперимента 75,2 ºС

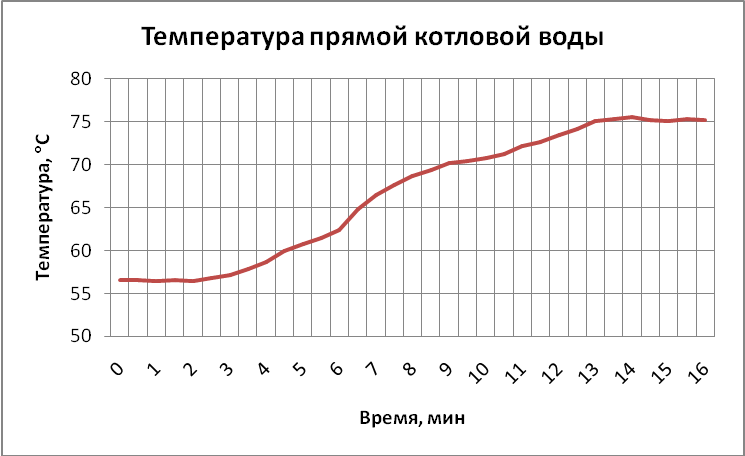
Рис.3.1.2. График изменения температуры котловой воды

Рис. 3.1.2. Переходная характеристика температуры воды.

Аппроксимация экспериментальной кривой была проведена методом моментов переходных функций, с использованием программы IDEN. В таблице 3.1 представлены значения, вводимые в программу.

Таблица 3.1. Значения экспериментальной аппроксимируемой кривой.

Время, мин

Температура, ºС

Время, мин

Температура, ºС

0
0,5
1
1,5
2
2,5
3
3,5
4
4,5
5
5,5
6
6,5
7
7,5

56,5
56,5
56,4
56,5
56,4
56,8
57,1
57,8
58,6
59,9
60,8
61,5
62,4
64,8
66,4
67,6

8
8,5
9
9,5
10
10,5
11
11,5
12
12,5
13
13,5
14
14,5
15
15,5
16

68,6
69,4
70,2
70,4
70,8
71,2
72,2
72,6
73,4
74,1
75
75,3
75,5
75,2
75,1
75,3
75,2

ПЕРЕДАТОЧНАЯ ФУНКЦИЯ АППРОКСИМИРУЮЩЕЙ МОДЕЛИ

K * Exp(-Tau*P)

W(P) = ----------------- .

1 + T*P

ПАРАМЕТРЫ МОДЕЛИ ОБЪЕКТА :

Коэффициент передачи K = 0.374

Постоянная времени T = 2.951 с

Запаздывание Tau = 4.450 с

НОРМИРОВАННЫЕ ПЕРЕХОДНЫЕ ФУНКЦИИ ОБЪЕКТА И МОДЕЛИ

Врем Объект Модель

0.000 0.000 0.000

0.500 0.000 0.000

1.000 -0.005 0.000

1.500 0.000 0.000

2.000 -0.005 0.000

2.500 0.016 0.000

3.000 0.032 0.000

3.500 0.070 0.000

4.000 0.112 0.000

4.500 0.182 0.017

5.000 0.230 0.170

5.500 0.267 0.299

6.000 0.316 0.409

6.500 0.444 0.501

7.000 0.529 0.579

7.500 0.594 0.644

8.000 0.647 0.700

8.500 0.690 0.746

9.000 0.733 0.786

9.500 0.743 0.819

10.000 0.765 0.848

10.500 0.786 0.871

11.000 0.840 0.891

11.500 0.861 0.908

12.000 0.904 0.923

12.500 0.941 0.935

13.000 0.989 0.945

13.500 1.005 0.953

14.000 1.016 0.961

14.500 1.000 0.967

15.000 0.995 0.972

15.500 1.005 0.976

16.000 1.000 0.980

ДИСПЕРСИЯ АДЕКВАТНОСТИ ДАННОЙ МОДЕЛИ ² = 0.003505

На рис.3.1.4 представлены графики нормированных переходных функций объекта и аппроксимирующей модели, а их значения сведены в таблицу.

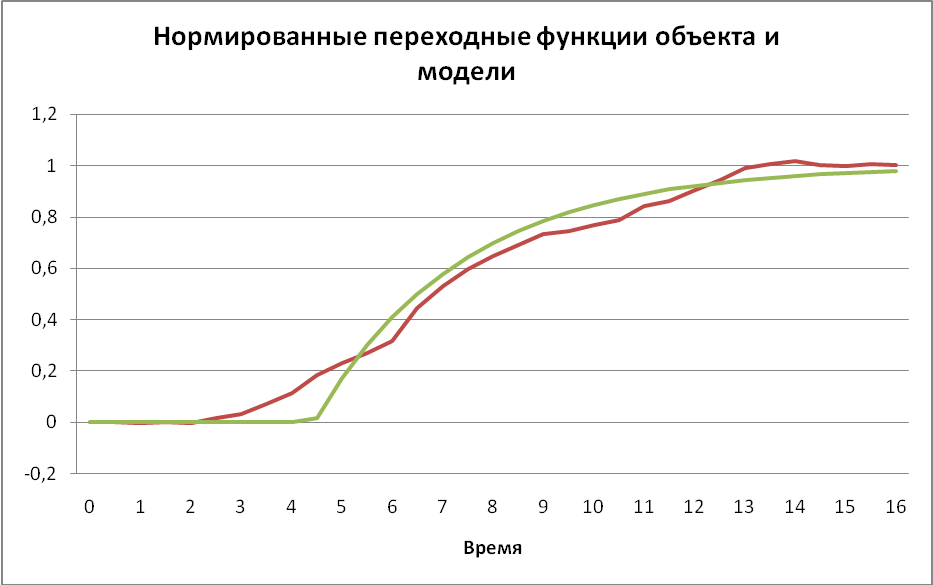
Рис.3.1.4. Переходные функции модели и объекта

2.Модель объекта по каналу возмущения (контур температуры обратной воды): зависимость температуры обратной воды от расхода газа. График входного возмущающего воздействия (температуры обратной воды) представлен на рис.3.1.5..

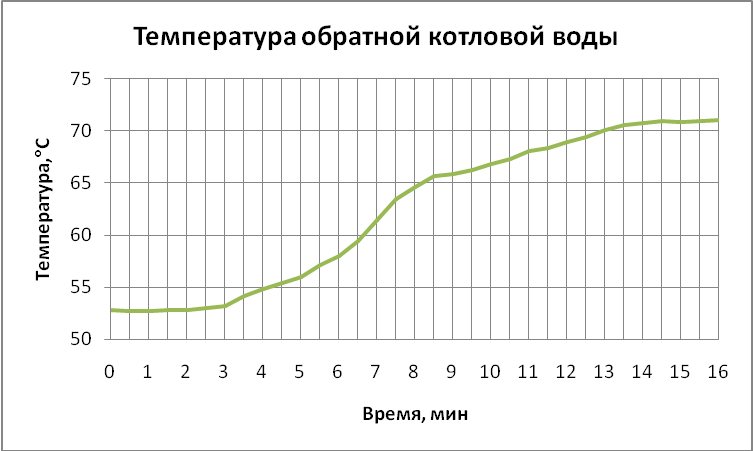
Рис.3.1.5. График изменения температуры обратной котловой воды

Параметры входного воздействия (расход газа) (рис.3.1.6):

значение входного воздействия до эксперимента = 0 м.куб/час

значение входного воздействия после эксперимента = 151,29 м.куб/час.

Рис.3.1.6

Параметры выходного сигнала объекта (температура воды):

среднее значение выходного сигнала до опыта = 52,8 ºС

установившееся среднее значение выходного сигнала после

эксперимента 70,9 ºС

Аппроксимация экспериментальной кривой была проведена также методом моментов переходных функций, с использованием программы IDEN. В таблице представлены значения, вводимые в программу.

Таблица . Значения экспериментальной аппроксимируемой кривой.

Время, мин

Температура, ºС

Время, мин

Температура, ºС

0
0,5
1
1,5
2
2,5
3
3,5
4
4,5
5
5,5
6
6,5
7
7,5

52,8
52,7
52,7
52,8
52,8
53
53,2
54,1
54,8
55,4
56
57,1
58
59,4
61,4
63,4

8
8,5
9
9,5
10
10,5
11
11,5
12
12,5
13
13,5
14
14,5
15
15,5
16

64,6
65,6
65,8
66,2
66,8
67,3
68
68,3
68,9
69,4
70,1
70,5
70,7
70,9
70,8
70,9
71

ПЕРЕДАТОЧНАЯ ФУНКЦИЯ АППРОКСИМИРУЮЩЕЙ МОДЕЛИ

K * Exp(-Tau*P)

W(P) = ----------------- .

1 + T*P

ПАРАМЕТРЫ МОДЕЛИ ОБЪЕКТА :

Коэффициент передачи K = 0.362

Постоянная времени T = 2.969

Запаздывание Tau = 4.629

ДИСПЕРСИЯ АДЕКВАТНОСТИ ДАННОЙ МОДЕЛИ = 0.002941

Таблица. Значения нормированных переходных функций объекта и модели.

Врем Объект Модель

0.000 0.000 0.000

0.500 -0.006 0.000

1.000 -0.006 0.000

1.500 0.000 0.000

2.000 0.000 0.000

2.500 0.011 0.000

3.000 0.022 0.000

3.500 0.072 0.000

4.000 0.110 0.000

4.500 0.144 0.000

5.000 0.177 0.118

5.500 0.238 0.254

6.000 0.287 0.370

6.500 0.365 0.468

7.000 0.475 0.550

7.500 0.580 0.620

8.000 0.652 0.679

8.500 0.707 0.729

9.000 0.718 0.771

9.500 0.740 0.806

10.000 0.773 0.836

10.500 0.801 0.862

11.000 0.840 0.883

11.500 0.856 0.901

12.000 0.890 0.916

12.500 0.917 0.929

13.000 0.956 0.940

13.500 0.978 0.950

14.000 0.989 0.957

14.500 1.000 0.964

15.000 1.011 0.970

15.500 1.000 0.974

16.000 1.006 0.978

На рис.3.1.7 представлены графики нормированных переходных функций объекта (котла) и аппроксимирующей модели, а их значения сведены в таблицу.

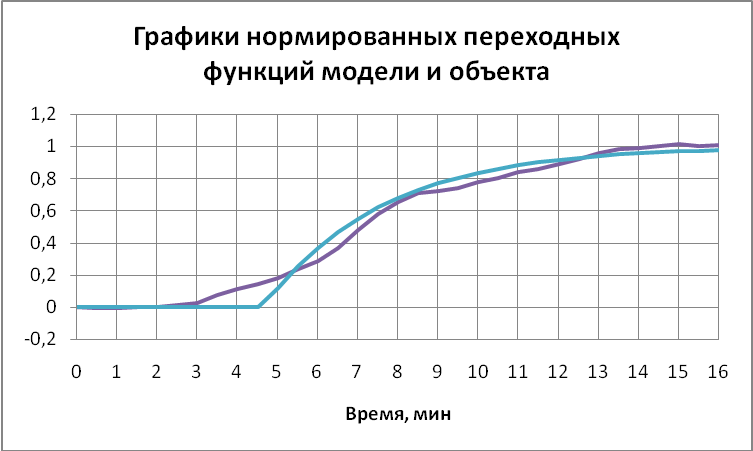
Рис. 3.1.6. Графики нормированных передаточных функций модели и объекта