Практикалық жұмыс №4.

MS Excel көмегімен берілген дифференциалдық теңдеу шешімін табу.

y¹=y/(e^-x+y^2), (x0=1, y0=1, [0,1], h=0.1);

Физикалық процесстердің математикалық модельдері көбіне дифференциалдық теңдеулер түрінде беріледі:

Y¹=f(x,y) [a,b] аралығында ; y(a)=y₀

Дифференциалдық теңдеуді шешудің негізгі екі әдісі қарастырылады:

1.Эйлер әдісі.

y_i+1=f(x_i,y_i)h+y_i[a,b] аралығында; у(а)=у₀ формуласы бойынша

2.Рунге-Кутта әдісі.

y_i+1=y_i+h/6(k₁+2k₂+2k₃+k₄), i=0,1,2, формуласы бойынша.

Мұндағы

k₁=f(x_i,y_i); k₂=f(x_i+h/2,y_i+h₁k₁/2);

k₃=f(x_i+h/2, y_i+hk₂/2); k₄=f(x_i+h, y_i+hk₃);

1.Эйлер әдісі.

у¹=y/(e^-x+y^2), (у0=1,[0,1],h=0.1);

Есепті шешу үшін Эйлер формуласы пайдаланылады:

f(x,y)=y/(e^-x+y^2)

y_i+1=(√e^-x+yi)h+y_i

[0.1] аралығында; y(a)=y₀;

A3:A12 ұяшықтарына 0.1 қадамымен х мәндері енгізіледі. B3 ұяшығына бастапқы шарты енгізіледі; B4 ұяшығына Эйлер формуласы енгізіледі- B4(=0.1*(1+A3^2+B3)^(1/2)+B3);

y1=y/e^-x+y^2
x	y	h
1	1	0,01
1,01	7,1
1,02	-23,3
1,03	128,8
1,04	-631,6
1,05	3170,5
1,06	-15839,9
1,07	79212,2
1,08	-396048
1,09	1980254
1,1	-9901257

2.Рунге-Кутта әдісі.

y_i+1=y_i+h/6(k₁+2k₂+2k₃+k₄), i=0,1,2, формуласын қолданамыз.

Мұндағы

k₁=f(x_i,y_i); k₂=f(x_i+h/2, y_i+hk₁/2);

k₃=f(x_i+h/2, y_i+hk₂/2); k₄=f(x_i+h, y_i+hk₃);

A25:A34 ұяшықтарына 0.1 қадаммен х-тің мәндерін енгіземіз. B25 ұяшығына бастапқы шарты енгізіледі. Ары қарай көршілес ұяшықтарға k₁,k₂,k₃,k₄ мәндерін есептейтін формулалар жазылады. Соңында сол мәндерді қолданып у мәнін есептей аламыз.

					4.2 Tapsirma
x	y	k1	k2	k3	k4	h	h/2
1	2	#ДЕЛ/0!	#ДЕЛ/0!	#ДЕЛ/0!	#ДЕЛ/0!	0,05	0,025
1,01	#ДЕЛ/0!	#ДЕЛ/0!	#ДЕЛ/0!	#ДЕЛ/0!	#ДЕЛ/0!	0,05	0,025
1,03	3,8	-64,2693	-20,4724	-30,6927	-14,7031	0,05	0,025
1,04	0,586535	-7,47545	-3,17099	-4,02483	-2,2327	0,05	0,025
1,05	0,212763	-2,17952	-1,0933	-1,28088	-0,779	0,05	0,025
1,06	0,103787	-0,89008	-0,49917	-0,559	-0,36268	0,05	0,025
1,07	0,059283	-0,43777	-0,26595	-0,28958	-0,19725	0,05	0,025
1,08	0,037394	-0,2427	-0,15662	-0,16738	-0,11845	0,05	0,025
1,09	0,025259	-0,14637	-0,09902	-0,10445	-0,07624	0,05	0,025
1,1	0,017941	-0,09397	-0,06603	-0,06899	-0,05167	0,05	0,025

Практикалық жұмыс №5

конус формуласымен берілген бетті тұрғызу. Жұмыс мақсаты: MS Excel- де бетті тұрғызуды үйрену. Бетті тұрғызу үшін келесі әрекеттерді орындау керек:

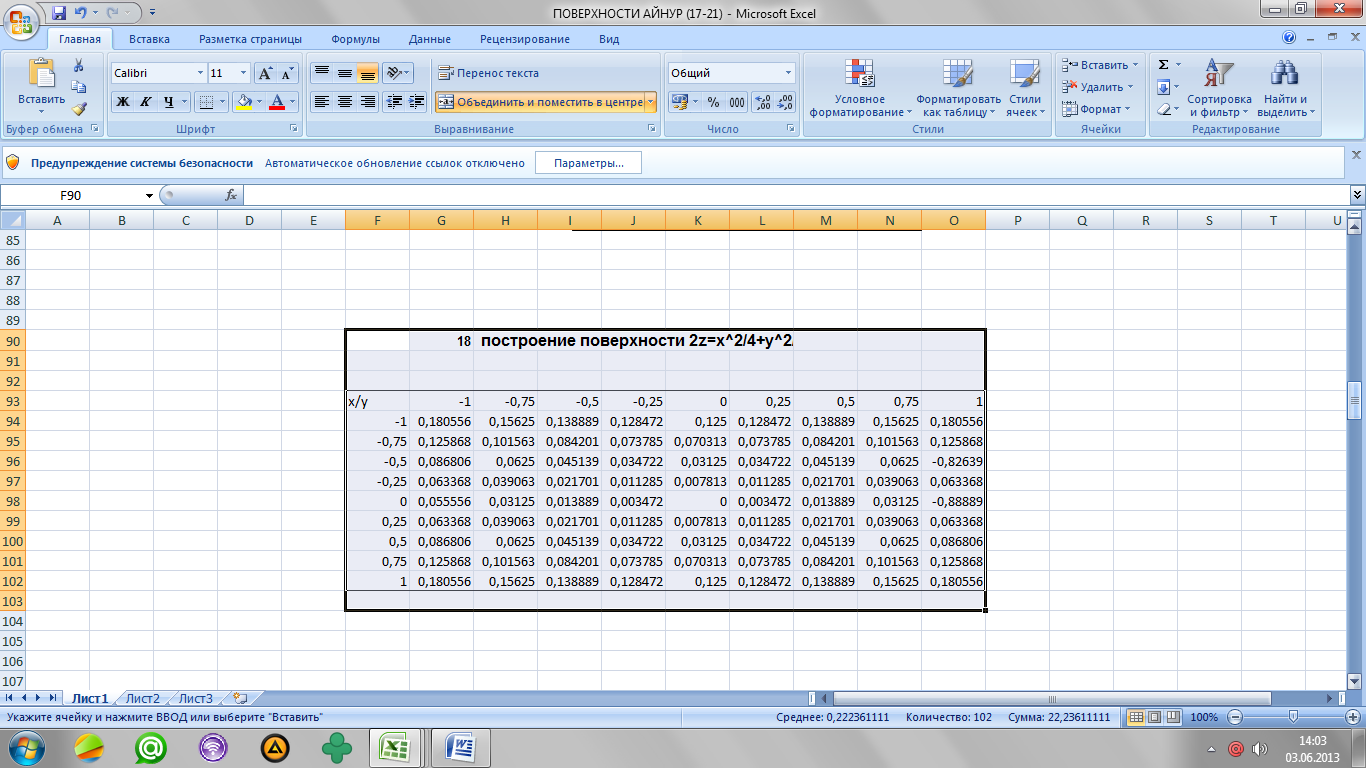
1.Екі координатасын өзгеруін біреуін дол бойынша, біреуін баған бойынша бір диапазонға жазу керек.

2.Координаталардың қиылысуында орналасқан ұяшыққа беттің формуласын енгізіп, автозаполнение командасы арқылы кестені толтырамыз.

3.Алынған мәліметтерді ерекшелеп алып, (тип диаграммы -Поверхность) бетті тұрғызамыз.

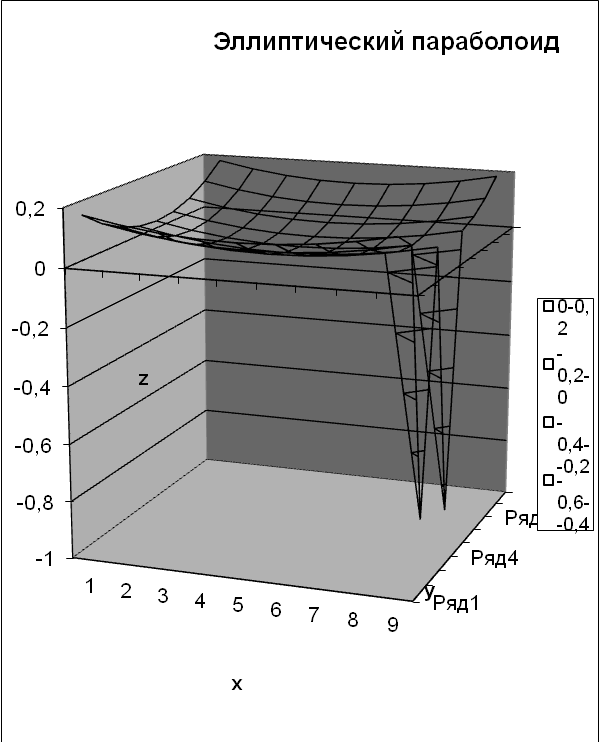
Практикалық жұмыс №6

Надстройка-Поиск решения көмегімен оптимизациялық тапсырманы орындау. Сызықтық программалаудың тапсырмасын келесі түрде көрсетуге болады:

Мақсат функцияның экстремумын табу:

F=c1x1+c2x2….+cnxn->max (min)

Айнымалылары шектелген теңдеу түрінде:

a11x1+a12x2+……..+a1n xn=b1;

………………………………….

an 1 xn+an2x2+……..+ann xn=bn;

Айнымалылары шектелген теңсіздік түрінде:

a11x1+a12x2+………+a1n xn <b1;

……………………………………

an1xn+an2x2+……….+ann xn<bn;