Алматы энергетика және байланыс университеті

Инженерлік кибернетика кафедрасы

Оқу- үйрену практикасы

№ 18 нұсқа

Орындаған: БАУк-12-3 тобының

студенті Уарбеков Б.Б

Тексерген: Калышев Н.Н

Алматы 2013

Мазмұны

Кіріспе....................................................................................................................3

1. Тапсырма. Теңдеулер шешімін табу.........................................................4

2. Тапсырма. Интегралды есептеу әдістері..................................................7

3. Тапсырма. Ең кіші квадрат әдісі...............................................................9

4. Тапсырма. MS Excel көмегімен дифференциалдық теңдеуді шешу әдістері.......................................................................................................11

5. Тапсырма. Беттерді тұрғызу....................................................................13

6. Тапсырма. Надстройки-Поиск решения көмегімен оптимизациялық тапсырманы орындау…...........................................................................14

7. Тапсырма. Ссылки и массивы функциясымен жұмыс істеу.................15

Қолданылған әдебиеттер тізімі..........................................................................19

Кіріспе.

Студенттер практика кезінде инженерлік есептерді шешудің әр түрлі әдістерін интегралды есептеу, дифференциалдық теңдеулерді есептеу меңгереді. Есептерді түрлі әдіспен шеше отырып MS Excel-дің математикалық, экономикалық есептерді шешудегі мүмкіндіктерін үйренеді. Студент әрбір тапсырмаға жазбаша есеп(отчет) береді. Есеп(отчет) төмендегідей болады:

Тапсырманың берілгені;

Әдістің түсіндірмесі;

Шешімнің кестелік түрі;

Жауабы;

Кейбір есептерді шешуде MS Excelмен қатар басқа алгоритмдік тілді қолдану қажет болады.

Практикалық жұмыс №1.

Берілген x⁴+cos x -2=0 теңдеуінің шешімін берілген әдістермен табу:

а) График көмегімен;

ә) Сандық итерация әдісімен;

б) Поиск решения құрылымының көмегімен;

с) С++ тілінде қақ бөлу әдісімен;

1. Графиктік әдісті қолданғанда теңдеудің алғашқы, барлық мүшелері бір жақта орналасқан түрін қолданған ыңғайлы.

Теңдік мынатүрде берілген

f (x)=x⁴+cos x -2

Электрондық кесте бағанына берілген 0<=x<=2 интервалындағы х-тің мәндерін енгіземіз, содан соң әрбір х мәні үшін f(x) мәні есептеледі. f(x) фунциясының графигі тұрғызылады.

1.1 - График арқылы түбірлерін іздеу

Графиктен көріп тұрғанымыздай, түбір x=1.1 нүктесінің маңында орналасқан. Бұл әдісті қолданғанда біз онша дәл шешім ала алмаймыз.

2) Жоғары дәлдікке ие болу үшін біз сандық итерация әдісін қолдана аламыз. Бұл әдісті қолданғанда біз алғашқы мән ретінде графиктік әдіс шешімін қолдана аламыз.

Сандық итерация әдісінің мәні алдыңғы қадамдағы мәнді келесі итерация үшін жорамал мән қолдануымызда жатыр. Бұл үшін біз теңдеудің алғашқы түрін x=(-cosx+2)^1/3 түріне келтіреміз.

Сол жақта тұрған мән есептелінетін мән деп аталады. Оны біз х_в деп белгілейміз. Оң жағындағы х жорамал мән деп аталады. x_n деп белгіленеді.

Xв=(-cosx+2)^1/3

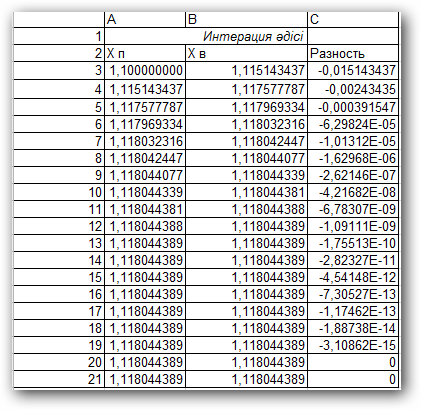
1.2 – Интерация әдісі

кестеден қарапайым итерация әдісі көмегімен х=1,118044389 түбірін бірнеше қадам ғана жасап тез табылғаны көрінеді

Қарапайым итерация әдісінің артықшылығы – ол электрондық кестеде оңай іске асырылады.Кемшілігі: кейде әдіс қиылыспайды – оның көмегімен барлық түбірлер табыла алмайды.

3) Поиск решения

Поиск решения надстройкасын іске қосу үшін Сервис-Надстройки-Поиск решения жолына түрткі қою керек.

надстройка поиск решения
бастапқы мән			1,118044389
формула			-1,6575E-09

1.3 – Поиск решения

Поиск решения көмегімен 1,11804458-ге тең түбір табылды

Поиск решения артықшылығы: қолдануы қарапайым және теңдеудің барлық түбірлерін табуға мүмкіндік береді

4.Қақ бөлу әдісі.

Қақ бөлу әдісінің [0,2] (a=0,b=2) интервалындағы f (x)=x⁴+cos x -2

функциясы үшін Turbo C++ программалау тіліндегі программа мәтіні.

#include<iostream.h>

#include<math.h>

#include<conio.h>

float f(float x)

{ float ff;

ff=pow(x,4)+cos(x)-2;

return ff;}

void main()

{ float a,b,c,fa,fc,eps; int n=0;

clrscr();

cin>>a>>b>>eps;

fa=f(a);

do

{ c=(a+b)/2;

fc=f(c);

if(fa*fc<0) b=c;

else

{ a=c; fa=fc;

} cout<<c<<endl; n=n+1;

} while (b-a>eps);

cout<<a<<endl;

cout<<n<<endl;}