1.3 Опцион на фьючерс
Теперь
в качестве базового актива для опциона
рассмотрим фьючерс.
Опционы на фьючерсы удобнее, чем опционы
на непосредственно базовые активы тех
же фьючерсов, потому что для работы с
ними отсутствует необходимость
прогнозировать дивиденды, оценивать
зарубежные процентные ставки и стоимость
хранения сырья/товаров. Фьючерсный
контракт: договор, заключенный в момент
времени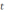 
о
поставке актива в будущем (время 
)
по цене 
.
Спотовая цена на не платящую дивиденды
акцию связана с фьючерсной ценой
следующим отношением:
Фьючерсную
цену в момент исполнения (время
)
можно выразить через цену фьючерса
,
известную во время
:
Соответственно формула теоретической цены европейского опциона Call и Put:
1.4 Опцион на маржируемый фьючерс
Расчеты по маржируемым опционам осуществляются по такой же схеме как по фьючерсам. Покупатель опциона не платит продавцу цену опциона при заключении сделки, вместо этого клиринговая палата биржи блокирует на его счету средства в размере гарантийного обеспечения (маржа). Продавец опциона также выставляет гарантийное обеспечение. По результатам каждого торгового дня алгоритмы клиринговой палаты определяют «расчетную цену». Положительная разница между сегодняшней и вчерашней расчетными маржируемого опциона начисляется на счет покупателя опциона и списывается со счета продавца. Отрицательная разница – наоборот.
В сущности, маржируемый опцион на фьючерс сам является является фьючерсным контрактом на прибыль от обычного опциона на фьючерс. Соответственно, теоретические цены для маржируемых европейских коллов и путов на фьючерсы определяются как:
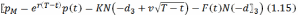
На
основе этих основополагающих допущений,
модель Блэка-Шоуза говорит, что цена
опциона является функцией текущей цены
базового актива(акции 
,
фьючерса
),
цены исполнения 
,
безрисковой процентной ставки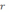 
,
времени до экспирации
,
волатильности цены базового актива
.
Все переменные не зависят от предпочтений
трейдеров к риску. Таким образом, модель
Блэка-Шоуза требует мало информации,
для вычисления цены опциона, и следовательно
не требует высоких вычислительных
мощностей для обработки модели.
Относительная простота применения
модели является причиной популярности
ее использования.
2.Улыбки волатильности
2.1 Подразумеваемая волатильность
Все параметры в модели Блэка-Шоуза, за исключением волатильности базового актива, можно непосредственно получить либо из рыночных данных либо из условий, предусмотренных опционным контрактом.
Таким образом, используя рыночную цену конкретного опциона можно легко получить рыночную оценку подразумеваемой волатильности его базового актива путем использования численных методов и «обращения» формулы Блэка-Шоуза. Подставляя подразумеваемую волатильность в модель Блэка-Шоуза, мы получаем цену опциона равную его рыночной стоимости.
2.2 Улыбка волатильности
Улыбка волатильности отражает связь между изменением подразумеваемой волатильности и изменением страйка опциона при фиксированной дате экспирации. Улыбка волатильности стала неким показателем ошибочности предположения модели Блэка-Шоуза о независимости волатильности от цены страйк.
Рассмотрим
фундаментальное предположение модели
Блэка-Шоуза о том, что базовый актив
имеет постоянную волатильность, и
следовательно, подразумеваемая
волатильность полученная численным
обращением формулы Блэка-Шоулза должна
быть одинаковой для опционов с одинаковыми
сроками экспирации, но с разными
страйками. Таким образом, если модель
Блэка-Шоуза права, то улыбка подразумеваемой
волатильности должна быть плоской. Эта
гипотеза подтверждалась некоторыми
эмпирическими данными. Подобная картина
была характерна до определенного времени
для опционов на индекс S&P 500 с одинаковыми
сроками экспирации и разными страйками,
то есть улыбка волатильности была
плоской, но подобная картина наблюдалась
только до краха 1987 года.
График 2.1.Улыбка волатильности
http://www.investopedia.com/terms/v/volatilitysmile.asp
Первые наблюдения эффекта подразумеваемой волатильности на рынке ценных бумаг показывали, что улыбка волатильности, как правило, была U-образной формы. Отметим тот факт, что уровень волатильности является относительно более низким для опционов при деньгах(около денег), и становится все более высоким для опционов в деньгах или вне денег.