1.2 Опцион на акции без дивидендов

Для начала рассмотрим формулу Блэка-Шоулза-Мертона для оценки европейских опционов колл и пут на акции, по которым не выплачиваются дивиденды. Мы предполагаем, что цены активов меняются непрерывно. Это значит, что даже за бесконечно малый промежуток времени они претерпевают изменения. Бесконечно малый промежуток времени обозначается как (дифференциал времени), соответствующее изменение цены актива обозначается как 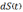. Поскольку мы рассматриваем акции (по которым не платятся дивиденды), логично предположить, что у них есть ожидаемая доходность – то есть что котировки на рынке формируются таким образом, чтобы держатель длинной позиции в акции ожидал получать от этой позиции средний доход в годовых. Мы предполагаем, что средняя доходность акции – это константа. Этот параметр также известен как дрифт акции.

Если бы акция была безрисковым инструментом (то есть если бы изменение цены не имело случайного компонента), то капитал держателя акции рос бы как банковский депозит с непрерывно начисляемыми процентами по ставке годовых.

Динамика цены акции описывалась бы дифференциальным уравнением , а значение цены акции в момент времени t определялось бы функцией .

Риск акций заключается в том, что фактическая доходность, которую они дают, практически всегда отличается от ожидаемой инвесторами. В половине случаев она оказывется больше ожидаемой, в половине – меньше. То, насколько сильно фактическая доходность может отличаться от ожидаемой, определяется параметром волатильность, которая обозначается буквой и равна стандартному отклонению логарифмической годовой доходности акции .

Мы предполагаем, что волатильность акции – это константа.

Соответственно, стохастическое дифференциальное уравнение динамики имеет вид:

Второе слагаемое этого уравнения, – это случайная величина, являющаяся с вероятностями 50/50 отклонением вверх или вниз, где размер отклонения составляет долларов. Где это дифференциал стохастического процесса Броуновского движения, обозначаемого как функция

Стохастическое дифференциальное уравнение, описывающее динамику цены акц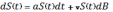ии имеет решение – функцию стохастического процесса цены акции

Блэк, Шоулз и Мертон доказали, что если мы предполагаем, что цена акции изменяется по описанному выше закону, то ее ожидаемая доходность не влияет на стоимость опциона. Следствием из этого заключения является необходимость находить ожидаемую стоимость опциона используя риск-нейтральное вероятностное распределение.

Сущность риск-нейтрального вероятностного распределения заключается в том, что мы считаем мат ожидание стоимости опциона так, как будто ожидаемая доходность акции (параметр ) равна безрисковой процентной ставке (параметр ). Риск-нейтральный подход также подразумевает, что ожидаемая будущая стоимость опциона должна дисконтироваться по безрисковой ставке, каким бы рискованным этот опцион ни был.

Далее приведем формулу теоретической цены европейского опциона Call:

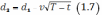
где  нормальная кумулятивная функция плотности вероятности, то есть вероятность того, что отклонение будет меньше в условиях стандартного нормального распределения (таким образом, и ограничивают область значений для функции стандартного нормального распределения).

Искомая формула теоретической цены европейского опциона Put: