2. Метод Лагранжа (метод вариации произвольных постоянных)

Пусть дано неоднородное линейное уравнение n-го порядка

y ⁽ⁿ⁾ + p₁ (x) y ^{(n – 1)} + … + p_{n – 1} (x) y ' + p_n (x) y = f (x),

где коэффициенты p₁ (x), …, p_n (x) и правая часть f (x) суть функции от x

непрерывные в некотором интервале (a, b).

Рассмотрим соответствующее однородное уравнение

z ⁽ⁿ⁾ + p₁ (x) z ^{(n – 1)} + … + p_{n – 1} (x) z ' + p_n (x) z = 0 (17)

Пусть z₁, z₂, …, z_n — фундаментальная система решений этого уравнения. Тогда

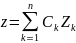
есть общее решение уравне ния (17)z ⁽ⁿ⁾ + p₁ (x) z ^{(n – 1)} + … + p_{n – 1} (x) z ' + p_n (x) z = 0. Решение данного неоднородного уравнения ищется в виде

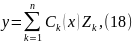
где функции C_k (x) определяются из системы уравнений

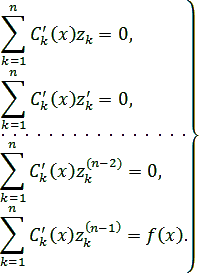
Решая эту систему относительно (k = 1, 2, …, n), находим

= φ_k(x) (k = 1, 2, …, n), откуда

C_k(x) = + C_k (k = 1, 2, …, n).

Подставляя найденные значения C_k (x) в формулу (18)y = C_k(x)z_k, получаем

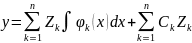
Это и есть общее решение уравнения. Все решения заведомо определены в интервале (a, b).

Рассмотрим пример на применение выше изложенного метода.

В примерах 1-3 найти общее решение неоднородного дифференциального уравнения.

Пример 1. [1, стр. 160], у''+4у' – 5у=х .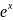

Характеристическое уравнение соответствующего однородного уравнения: k² + 4 k - 5 = 0. Его корни k₁= -5, k₂=1. Фундаментальная система решений y₁ = e ^-5x, y₂ = e ^x, y = C₁ e ^-5x + C₂ e^x. Ищем решение исходного уравнения в виде y(x) = C₁(x) e ^-5x + C₂(x)e^x. В соответствии с методом вариации система для нахождения

Будет 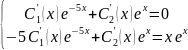, откуда

=

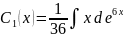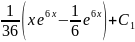
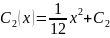
Общее решение у= 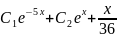(3х+1)

(константы в окончательном ответе переобозначены).

Решим примеры на применение метода Лагранжа.

Пример 2. [1, стр. 160], у'' – у= .

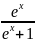Рассмотрим однородное уравнение у'' – у=0, характеристическое уравнение примет вид k² – k=0, корни которого k_1,2= ±1. Тогда у= С₁ е^х+С₂ е^-х.

= ,

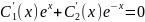
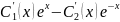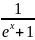Найдем (х)=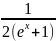

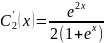
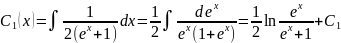
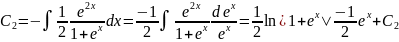
Общее решение уравнения будет

у= .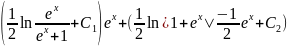

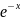Пример 3. [3, cтр. 155], у'' +у = .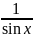

Рассмотрим однородное уравнение у'' +у'=0, характеристическое уравнение k²+1=0, корни которого k_1,2=±i, y=C₁ сos x +C₂ sin x.

Тогда

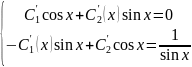, то С₁(х)= - х+С₁, С₂(х)=ln |sin x| +C₂.

Общее решение уравнения у= (С₁ – х) cos х+ (ln |sin x| +C₂) sin x.

Заключение

Дифференциальные уравнения занимают особое место в математике и имеют многочисленные приложения в большом спектре наук. Исследования природных процессов и изучение закономерностей общественных процессов приводят к построению математических моделей, основой которых являются дифференциальные уравнения.

В данной курсовой работе были изучены методы решения дифференциальных уравнений высших порядков с постоянными коэффициентами. В практической части работы были разобраны примеры на применение метода Эйлера, метода неопределенных коэффициентов, метода Лагранжа.

Была использована литература следующих авторов: П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова, Н.М. Матвеев, О.А. Олейник (статья), Н.П. Климова (статья) и электронные ресурсы.