4. Линейная зависимость функций

Рассмотрим уравнение

L(y) ≡ y ⁽ⁿ⁾ + а₁ (x) y ^{(n – 1)} + … + а_{n – 1} (x) y ' + а_n (x) y

Зная n частных решений y₁, y₂, …, y_n можно построить семейство решений, зависящее от n произвольных постоянных:

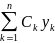
Это решение будет общим решением, если частные решения y₁, y₂, …, y_n обладают одним дополнительным свойством, относящимся к характеру зависимости между ними.

Прежде чем сформулировать это свойство, введем понятие о линейной независимости функций.

Пусть даны m функций от x:

y₁, y₂, …, y_m (a < x < b) (8)

Составим их линейную комбинацию с постоянными коэффициентами

a₁ y₁+a₂y₂+… +a_my_m.

Если эта линейная комбинация тождественно равна нулю в интервале (a, b): a₁ y₁+a₂y₂+… +a_my_m=0 (a < x < b), т. е. при нулевых значениях коэффициентов α₁, α₂, …, α_m то функции (8)y₁, y₂, …, y_m (a < x < b) называются линейно независимыми в интервале (a, b). В противном случае функции (8)y₁, y₂, …, y_m (a < x < b) называются линейно зависимыми в этом интервале. Две функции y₁ и y₂ линейно независимы в интервале (a, b), если

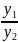≠ const   (a < x < b).

Теорема 1. Если функции (8)y₁, y₂, …, y_m (a < x < b) линейно зависимы в интервале (a, b), то одна из них является линейной комбинацией остальных.

Совокупность n решений

α₁, α₂, …, α_n (a < x < b) (9)

однородного линейного уравнения L(y) = 0, линейно независимых в интервале (a, b), называется фундаментальной системой решений этого уравнения в интервале (a, b). (Теорему примем без доказательства.)

Дадим признак линейной независимости n частных решений α₁, α₂, …, α_n   (a < x < b) однородного линейного уравнения n-го порядка. С этой целью введем в рассмотрение определитель, составленный из данных частных решений и их производных до порядка (n – 1) включительно:

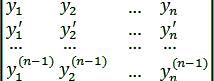
Этот определитель называется определителем Вронского решений y₁, y₂, …, y_n и обозначается W(x).

Теорема 2. Для того чтобы решения (9)α₁, α₂, …, α_n   (a < x < b) были линейно независимы в (a, b), т. е. в интервале непрерывности коэффициентов уравнения L(y) = 0, необходимо и достаточно, чтобы W(x) не обращался в нуль ни в одной точке из (a, b). (Теорему примем без доказательства.)

Значение определителя Вронского n решений однородного линейного уравнения L(y) = 0 тесно связано с самим уравнением, а именно: имеет место следующая формула Остроградского—Лиувилля:

W(x) = W(x₀) (10)

Из формулы (10)W(x) = W(x₀) видно, что определитель Вронского n решений уравнения L(y) = 0 обладает двумя замечательными свойствами:

1. Если W(x) обращается в нуль в одной точке из интервала (a, b), то он равен нулю во всех точках этого интервала.

2. Если W(x) не равен нулю в одной точке из интервала (a, b), то он отличен от нуля во всех точках этого интервала.

Таким образом, для того, чтобы n решений (10)α₁, α₂, …, α_n   (a < x < b) составляли фундаментальную систему решений уравнения L(y) = 0 в интервале (a, b), достаточно, чтобы их определитель Вронского был отличен от нуля в одной точке x₀ ∈ (a, b). [4]