
Вариант 9
№ |
Задание |
Оценка в баллах |
|
|
Найти
частные производные и полный дифференциал
функции z
= sin |
1 |
|
|
Исследовать
данную функцию на экстремум z
=
|
3 |
|
|
. Написать уравнения касательной плоскости и нормали к заданной поверхности x(y+z)(xy-z) = 8 в точке M0(2,1,3). |
1 |
|
|
Найдите прямоугольник периметра 12 см, который вращением вокруг одной из сторон образует тело наибольшего объема. |
3 |
|
|
Найти производную функции z = y2- 3x –y в точке М (1, -1) в направлении градиента функции z. |
1 |
|
|
Оцените
абсолютную и относительную погрешность
при вычислении значения функции z
=
|
1 |
Вариант 10
№ |
Задание |
Оценка в баллах |
|
|
Найти
частные производные и полный дифференциал
функции z
= arccos |
1 |
|
|
Исследовать
данную функцию на экстремум z
=
|
3 |
|
|
. Написать уравнения касательной плоскости и нормали к заданной поверхности z
=
|
1 |
|
|
В прямой круговой конус радиусом основа-ния 6 и высотой 10 впишите прямоугольный параллелепипед наибольшего объема. |
3 |
|
|
Найти производную функции z = 5x2 – 2y + 4 в точке М (1, -2) в направлении градиента функции z. |
1 |
|
|
Оцените
абсолютную и относительную погрешность
при вычислении значения функции z
=
|
1 |
Вариант 11
№ |
Задание |
Оценка в баллах |
|
|
Найти
частные производные и полный дифференциал
функции z
= x2·sin |
1 |
|
|
Исследовать данную функцию на экстремум z =1- . |
3 |
|
|
. Написать уравнения касательной плоскости и нормали к заданной поверхности
|
1 |
|
|
В шар радиуса 10 впишите цилиндр наибольшего объема. |
3 |
|
|
Найти производную функции z = x2- 2x – 4y в точке М (1, 0) в направлении градиента функции z. |
1 |
|
|
Оцените
абсолютную и относительную погрешность
при вычислении значения функции z
=
|
1 |
Вариант 12
№ |
Задание |
Оценка в баллах |
|
|
Найти
частные производные и полный дифференциал
функции z
=
|
1 |
|
|
Исследовать
данную функцию на экстремум z
= |
3 |
|
|
. Написать уравнения касательной плоскости и нормали к заданной поверхности
|
1 |
|
|
Найти стороны прямоугольного треуголь-ника, имеющего при данной площади 8 наименьший периметр. |
3 |
|
|
Найти производную функции z = x- 2y – 2y2 в точке М (2, -2) в направлении градиента функции z. |
1 |
|
|
Оцените
абсолютную и относительную погрешность
при вычислении значения функции z
=
|
1 |

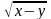 .
. .
.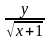 в точке x=3,05,
y=2,02.
в точке x=3,05,
y=2,02.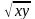 .
.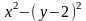 .
. в точке M0(1,2,5).
в точке M0(1,2,5). в точке x=
в точке x=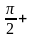 0,01,
y=
0,01,
y= 0,03.
0,03.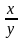 .
. в
точке M0
(1,1,1).
в
точке M0
(1,1,1).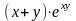 в точке x=1,02,
y=1,2.
в точке x=1,02,
y=1,2. .
. .
.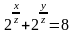 в
точке M0
(2,2,1).
в
точке M0
(2,2,1). в точке x=1,02,
y=e+0,1.
в точке x=1,02,
y=e+0,1.