
Вариант 1
№ |
Задание |
Оценка в баллах |
|
|
Найти
частные производные и полный дифференциал
функции z
= - |
1 |
|
|
Исследовать
данную функцию на экстремум z
=
|
3 |
|
|
.
Написать уравнения касательной
плоскости и нормали к заданной
поверхности z
=
|
1 |
|
|
Найти наибольший объем параллелепипеда при данной сумме 12 всех его ребер. |
3 |
|
|
Найти производную функции z = 5x2 - 3x – y в точке М (2, 1) в направлении градиента функции z. |
1 |
|
|
Оцените
абсолютную и относительную погрешность
при вычислении значения функции z
=
|
1 |
Вариант 2
№ |
Задание |
Оценка в баллах |
|
|
Найти
частные производные и полный дифференциал
функции z
= z= |
1 |
|
|
Исследовать
данную функцию на экстремум z
= |
3 |
|
|
. Написать уравнения касательной плоскости и нормали к заданной поверхности z
=
|
1 |
|
|
При каких размерах открытая прямоугольная ванна вместимостью 4 м3 имеет наименьшую поверхность? |
3 |
|
|
Найти производную функции z = 2x2- 3x – 6y в точке М (1, 2) в направлении градиента функции z. |
1 |
|
|
Оцените
абсолютную и относительную погрешность
при вычислении значения функции z
=
|
1 |
Вариант 3
№ |
Задание |
Оценка в баллах |
|
|
Найти
частные производные и полный дифференциал
функции z
= arcsin |
1 |
|
|
Исследовать
данную функцию на экстремум z
=
|
3 |
|
|
.
Написать уравнения касательной
плоскости и нормали к заданной
поверхности z
=
|
1 |
|
|
В полушар радиуса 5 впишите прямоуголь-ный параллелепипед наибольшего объема. |
3 |
|
|
Найти производную функции z = 5y2- 3x – 2y в точке М (1, 1) в направлении градиента функции z. |
1 |
|
|
Оцените
абсолютную и относительную погрешность
при вычислении значения функции z
=
|
1 |
Вариант 4
№ |
Задание |
Оценка в баллах |
|
|
Найти
частные производные и полный дифференциал
функции z
=
|
1 |
|
|
Исследовать
данную функцию на экстремум z
= |
3 |
|
|
. Написать уравнения касательной плоскости и нормали к заданной поверхности z
=
|
1 |
|
|
Найдите прямоугольный параллелепипед с длиной диагонали 12, имеющий наибольший объем. |
3 |
|
|
Найти производную функции z = 2y2- x – 4y в точке М (3, 2) в направлении градиента функции z. |
1 |
|
|
Оцените
абсолютную и относительную погрешность
при вычислении значения функции z
=
|
1 |

 arccos
arccos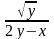 .
.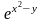 (5
- 2x
- y),
x
> 0, y
> 0.
(5
- 2x
- y),
x
> 0, y
> 0.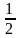 arctg
arctg в точке M0
(1, 1,
в точке M0
(1, 1,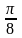 ).
). в точке x=1,02,
y=0,97.
в точке x=1,02,
y=0,97.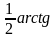
 .
.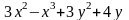 .
.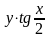 в
точке M0
(
в
точке M0
( ,
2, 2).
,
2, 2). в точке x=2,02,
y=3,03.
в точке x=2,02,
y=3,03. .
.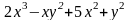 .
. в точке M0(
в точке M0( ,
,
).
,
,
). в точке x=3,1,
y=4,2.
в точке x=3,1,
y=4,2.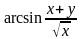 .
. .
.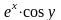 в
точке M0
(1,
в
точке M0
(1,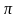 ,
, ).
). в точке x=4,01,
y=10,98.
в точке x=4,01,
y=10,98.