
- •Уравнение Мещерского -
- •Период колебаний пружинного маятника - зависит от жёсткости пружины: с увеличением коэффициента жёсткости пружины период колебания маятника уменьшается
- •21.Первый закон термодинамики.
- •22.Термодинамика изопроцессов.
- •26.Уравнение Ван дер вальса.
- •27. Фазовые переходы первго и второго рода.
Период колебаний пружинного маятника - зависит от жёсткости пружины: с увеличением коэффициента жёсткости пружины период колебания маятника уменьшается
![]() Пружинный
маятник — это груз, колеблющийся на
пружине. Он совершает возвратно-поступательное
движение. Пружинный маятник подчиняется
законам движения, по которым можно
определить период его колебаний, зная
массу груза и жесткость пружины. Период
колебаний пружинного маятника не зависит
от места его расположения и амплитуды
колебаний.
Период
колебаний математического маятника
Математический
маятник –
материальная точка, подвешенная на
невесомой нерастяжимой нити (физическая
модель).
Пружинный
маятник — это груз, колеблющийся на
пружине. Он совершает возвратно-поступательное
движение. Пружинный маятник подчиняется
законам движения, по которым можно
определить период его колебаний, зная
массу груза и жесткость пружины. Период
колебаний пружинного маятника не зависит
от места его расположения и амплитуды
колебаний.
Период
колебаний математического маятника
Математический
маятник –
материальная точка, подвешенная на
невесомой нерастяжимой нити (физическая
модель).
Период
колебаний
|
|
Важнейший вывод: период колебаний математического маятника не зависит от массы тела! |
|
Период колебаний физического маятника - Физическим маятником называется твердое тело, которое может качаться вокруг неподвижной оси.
при
малых колебаниях физический маятник
совершает гармонические колебания с
циклической частотой ω0 и
периодом
![]() Кинетическая
и потенциальная энергии колебательной
системы - При
свободных механических колебаниях
кинетическая и потенциальная энергии
изменяются периодически. При максимальном
отклонении тела от положения равновесия
его скорость, а следовательно, и
кинетическая энергия обращаются в нуль.
В этом положении потенциальная энергия
колеблющегося тела достигает максимального
значения. Для груза на горизонтально
расположенной пружине потенциальная
энергия – это энергия упругих деформаций
пружины. Для математического маятника
– это энергия в поле тяготения Земли.Когда
тело при своем движении проходит через
положение равновесия, его скорость
максимальна. В этот момент оно обладает
максимальной кинетической и минимальной
потенциальной энергией. Увеличение
кинетической энергии происходит за
счет уменьшения потенциальной энергии.
При дальнейшем движении начинает
увеличиваться потенциальная энергия
за счет убыли кинетической энергии и
т. д.Таким образом, при
гармонических колебаниях происходит
периодическое превращение кинетической
энергии в потенциальную и наоборот.Закон
сохранения при колебательном движении-
Когда
маятник отклоняют на высоту h,
его потенциальная
энергия максимальная.
Когда маятник опускается, потенциальная
энергия переходит в кинетическую.
Причем в нижней точке, где потенциальная
энергия равна нулю, кинетическая энергия
максимальная и равна потенциальной
энергии в верхней точке. Скорость груза
в этой точке максимальная.
Кинетическая
и потенциальная энергии колебательной
системы - При
свободных механических колебаниях
кинетическая и потенциальная энергии
изменяются периодически. При максимальном
отклонении тела от положения равновесия
его скорость, а следовательно, и
кинетическая энергия обращаются в нуль.
В этом положении потенциальная энергия
колеблющегося тела достигает максимального
значения. Для груза на горизонтально
расположенной пружине потенциальная
энергия – это энергия упругих деформаций
пружины. Для математического маятника
– это энергия в поле тяготения Земли.Когда
тело при своем движении проходит через
положение равновесия, его скорость
максимальна. В этот момент оно обладает
максимальной кинетической и минимальной
потенциальной энергией. Увеличение
кинетической энергии происходит за
счет уменьшения потенциальной энергии.
При дальнейшем движении начинает
увеличиваться потенциальная энергия
за счет убыли кинетической энергии и
т. д.Таким образом, при
гармонических колебаниях происходит
периодическое превращение кинетической
энергии в потенциальную и наоборот.Закон
сохранения при колебательном движении-
Когда
маятник отклоняют на высоту h,
его потенциальная
энергия максимальная.
Когда маятник опускается, потенциальная
энергия переходит в кинетическую.
Причем в нижней точке, где потенциальная
энергия равна нулю, кинетическая энергия
максимальная и равна потенциальной
энергии в верхней точке. Скорость груза
в этой точке максимальная.
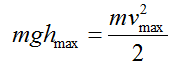
Билет №14
Затухающие колебания – колебания, энергия которых уменьшается с течением времени
Дифференциальное
уравнение свободных затухающих
колебаний линейной
системы задается
в виде
![]() где
s — колеблющаяся величина, описывающая
тот или иной физический процесс,
=const
— коэффициент
затухания, 0 —
циклическая частота
свободных незатухающих колебаний
той же колебательной системы, т. е.
при =0
(при отсутствии потерь энергии)
называется собственной
частотойколебательной
системы.
где
s — колеблющаяся величина, описывающая
тот или иной физический процесс,
=const
— коэффициент
затухания, 0 —
циклическая частота
свободных незатухающих колебаний
той же колебательной системы, т. е.
при =0
(при отсутствии потерь энергии)
называется собственной
частотойколебательной
системы.
Решение уравнения имеет вид:
![]() Периодом
затухающих колебаний называется
минимальный промежуток времени, за
который система проходит дважды положение
равновесия в одном направлении.Период
затухающих колебаний:
Периодом
затухающих колебаний называется
минимальный промежуток времени, за
который система проходит дважды положение
равновесия в одном направлении.Период
затухающих колебаний:
![]() .Смысл,
который вкладывался в понятие периода
для незатухающих колебаний, не подходит
для затухающих колебаний, так как
колебательная система никогда не
возвращается в исходное состояние из-за
потерь колебательной энергии. При
наличии трения колебания идут медленнее:
.Смысл,
который вкладывался в понятие периода
для незатухающих колебаний, не подходит
для затухающих колебаний, так как
колебательная система никогда не
возвращается в исходное состояние из-за
потерь колебательной энергии. При
наличии трения колебания идут медленнее: ![]() .
.
Декремент затухания – характеристика быстроты затухания колебаний: d = ln(A1/A2), где А1 и А2 - амплитуды двухколебаний, следующих друг за другом в одну и ту же сторону. Добротность затухания - Важной характеристикой колебательной системы, совершающей свободные затухающие колебания, является добротность Q. Этот параметр определяется как число N полных колебаний, совершаемых системой за время затухания τ, умноженное на π: Чем медленнее происходит затухание свободных колебаний, тем выше добротность Q колебательной системы
№15Вынужденные колебания - колебания, происходящие под воздействием внешних сил, меняющихся во времени.
Второй закон Ньютона для т осциллятора (маятника) запишется в виде:
![]()
Если
![]()
и заменить ускорение на вторую производную от координаты по времени, то получим следующее дифференциальное уравнение:
![]()
Общее решение однородного уравнения:
![]()
где
A,φ произвольные постоянныеНайдём
частное решение. Подставим в уравнение
решение вида:
![]() и получим значение для константы:
и получим значение для константы:
![]() Тогда
окончательное решение запишется в виде:
Тогда
окончательное решение запишется в виде:
![]()
При совпадении частоты внешней силы и частоты собственных колебаний тела амплитуда вынужденных колебаний резко возрастает. Такое явление называют механическим резонансом.Резона́нс— явление резкого возрастания амплитуды вынужденных колебаний.Увеличение амплитуды — это лишь следствие резонанса, а причина — совпадение внешней частоты с внутренней частотой колебательной системы.Резонансная частота – частота, в которой амплитуда максимальна (немного меньше собственной частоты)
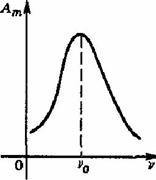 График
зависимости амплитуды вынужденных
колебаний от частоты вынуждающей силы
называется резонансной
кривой.В
зависимости от коэффициента затухания
получаем семейство резонансных кривых,
чем коэффициент, меньше тем кривая
больше и выше.
График
зависимости амплитуды вынужденных
колебаний от частоты вынуждающей силы
называется резонансной
кривой.В
зависимости от коэффициента затухания
получаем семейство резонансных кривых,
чем коэффициент, меньше тем кривая
больше и выше.
Амплитуда зависит от частоты вынужденных колебаний, если частота равняет резонансной частоте, то амплитуда максимальнее. Так же зависит от коэффициента затухания, если он равнее 0, то амплитуда бесконечна.Фа́за колеба́ний — аргумент периодически изменяющейся функции, описывающей колебательный или волновой процесс. ὼ0е+ᵩ
Билет №16
Сложение нескольких гармонических колебаний одного направления и одинаковой частоты становится наглядным, если изображать колебания графически в виде векторов на плоскости. Полученная таким способом схема называется векторной диаграммой.
Рассмотрим сложение двух гармонических колебаний одного направления и одинаковой частоты:
![]()
![]()
Представим
оба колебания с помощью векторов A1и
А2. Построим по правилам сложения векторов
результирующий вектор А, проекция этого
вектора на ось x
равна сумме проекций складываемых
векторов:
![]()
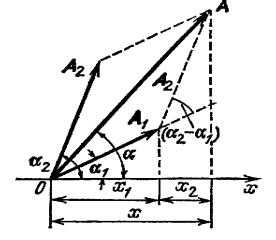
Поэтому, вектор A представляет собой результирующее колебание. Этот вектор вращается с той же угловой скоростью как и векторы А1 и А2, так что сумма x1 и х2 является гармоническим колебанием с такой же частотой, амплитудой и фазой.Используя теорему косинусов получаем, что
![]()
![]() Представление
гармонических колебаний с помощью
векторов позволяет заменить сложение
функций сложением векторов, что
значительно проще.
Представление
гармонических колебаний с помощью
векторов позволяет заменить сложение
функций сложением векторов, что
значительно проще.
При сложении двух гармонических колебаний разной частоты, происходящих в одном направлении, возникает негармоническое колебание.
Сложение колебаний разной частоты
Результирующее
отклонение в каждый момент времени
также равно алгебраической сумме
отклонений составляющих колебаний.
С
другой стороны, любые негармонические
колебания можно рассматривать как
результирующее ряда гармонических
колебаний и разложить его на эти
составляющие. Соответствующий
математический прием носит название
анализа Фурье.Биения
- колебания с периодически меняющейся
амплитудой, возникающие в результате
наложения двух гармонических колебаний
с несколько различными, но близкими
частотами.Сложение
взаимно перпендикулярных колебаний:Колебания
в двух взаимно перпендикулярных
направлениях происходят независимо
друг от друга:![]() Здесь
собственные частоты гармонических
колебаний равны:
Здесь
собственные частоты гармонических
колебаний равны:![]() Рассмотрим траекторию движения грузов:
Рассмотрим траекторию движения грузов:
![]()
в ходе преобразований получим:
![]()
Таким
образом, груз будет совершать периодические
движения по эллиптической траектории.
Направление движения вдоль траектории
и ориентация эллипса относительно осей
зависят от начальной разности фаз
![]()
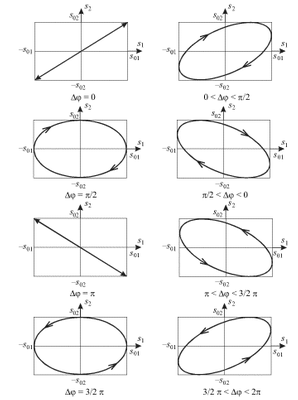
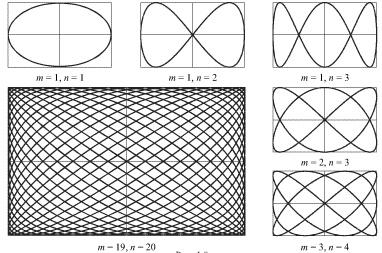
Если частоты двух взаимно-перпендикулярных колебаний не совпадают, но являются кратными, то траектории движения представляют собой замкнутые кривые, называемые фигурами Лиссажу. Отметим, что отношение частот колебаний равно отношению чисел точек касания фигуры Лиссажу к сторонам прямоугольника, в который она вписана.
Билет №17
Понятие потока – объем жидкости, протекающая в единицу времени через некоторую воображаемую площадку.
ΔΦ=VcosαΔS=(V⃗ ⋅n⃗ )ΔS=VnΔS . (2)
где (V⃗ ⋅n⃗ )=Vcosα - скалярное произведение векторов V⃗ и n⃗ ; Vn - нормальная к площадке компонента вектора скорости
Трубка
тока – это
часть жидкости, ограниченная линиями
тока. Частицы жидкости при своём движении
не пересекают стенок трубки тока.
Линии
тока - это
линии, проведённые в движущейся жидкости
так, что касательные к ним в каждой точке
совпадают по направлению с вектором
скорости![]() . Густота
линий тока пропорциональна величине
скорости в данном месте.Под потоком
жидкости понимают
движущуюся массу жидкости, полностью
или частично ограниченную поверхностями.
Поверхности раздела могут быть твердыми
или образованными самой жидкостью на
границе раздела фаз. Из-за сложности
учета влияния всех факторов при движении
потока действительное движение жидкости
заменяют упрощенной моделью. В основе
изучения гидродинамики лежит так
называемая струйчатая
модель движения. Эта
схема предполагает, что поток жидкости
состоит из бесконечно большого числа
элементарных струек. Живым
сечением потока называется
площадь сечения потока, проведенного
перпендикулярно к направлению линий
тока и ограниченного его внешним
контуром. Площадь живого сечения потока
равна сумме площадей живых сечений
элементарных струек. Стационарное
течение идеальной жидкости. Течение
жидкости представляет собой поле
скоростей, изображенное с помощью линий
тока. Если
поле скоростей, то есть форма
и расположение соответствующие
ему линии тока не меняются с течением
времени, то движение жидкости
называется стационарным или установившимся.
. Густота
линий тока пропорциональна величине
скорости в данном месте.Под потоком
жидкости понимают
движущуюся массу жидкости, полностью
или частично ограниченную поверхностями.
Поверхности раздела могут быть твердыми
или образованными самой жидкостью на
границе раздела фаз. Из-за сложности
учета влияния всех факторов при движении
потока действительное движение жидкости
заменяют упрощенной моделью. В основе
изучения гидродинамики лежит так
называемая струйчатая
модель движения. Эта
схема предполагает, что поток жидкости
состоит из бесконечно большого числа
элементарных струек. Живым
сечением потока называется
площадь сечения потока, проведенного
перпендикулярно к направлению линий
тока и ограниченного его внешним
контуром. Площадь живого сечения потока
равна сумме площадей живых сечений
элементарных струек. Стационарное
течение идеальной жидкости. Течение
жидкости представляет собой поле
скоростей, изображенное с помощью линий
тока. Если
поле скоростей, то есть форма
и расположение соответствующие
ему линии тока не меняются с течением
времени, то движение жидкости
называется стационарным или установившимся.
Уравнение
неразрывности бернулли и Стокса:
![]()
Из уравнения Бернулли следует, что при увеличении скорости течения (уменьшении сечения трубы) динамическое давление жидкости возрастает, а ее статическое давление уменьшается. Как видно из его вывода, уравнение Бернулли — выражение закона сохранения энергии применительно к установившемуся течению идеальной жидкости. Оно хорошо выполняется и для реальных жидкостей, внутреннее трение которых не очень велико. Уравнения Навье — Стокса (Шаблон:Lang-en) — система дифференциальных уравнений в частных производных, описывающая движение вязкой жидкости. Уравнения Навье — Стокса являются одними из важнейших в гидродинамике и применяются в математическом моделировании многих природных явлений и технических задач. Названы по имени французского физика Луи Навье и британского математика Джорджа Стокса. Система состоит из двух уравнений: уравнения неразрывности,уравнения движения.В векторном виде для несжимаемой жидкости они записываются следующим образом:
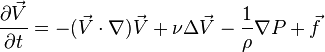
![]() где:
где: ![]() - оператор
Гамильтона, Δ - оператор
Лапласа,
- оператор
Гамильтона, Δ - оператор
Лапласа, ![]() -
вектор скорости, t -
время, ν -
коэффициент кинематической вязкости, ρ -
плотность, P - давление,
-
вектор скорости, t -
время, ν -
коэффициент кинематической вязкости, ρ -
плотность, P - давление, ![]() -
вектор плотности массовых сил.
Ньютоновские жидкости, уравнение –
подчиняются уравнению Ньютона.
-
вектор плотности массовых сил.
Ньютоновские жидкости, уравнение –
подчиняются уравнению Ньютона.
Для них вязкость ( )не зависит от градиента скорости (dv/dx)Примеры: вода, спирт, плазма крови , низкомолекулярные
органические жидкости Простое уравнение, описывающее силы вязкости в ньютоновской жидкости, во многом определяющие ее поведение, основано на сдвиговом течении:
![]() ,где:
,где:![]() — касательное
напряжение,
вызываемое жидкостью, Па;
— касательное
напряжение,
вызываемое жидкостью, Па;![]() —
динамический коэффициент вязкости —
коэффициент
—
динамический коэффициент вязкости —
коэффициент
пропорциональности, Па·с;
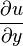 —
производная
скорости в направлении, перпендикулярном
направлению сдвига, с−1.Это
уравнение обычно используют при течении
жидкости в одном направлении, когда
вектор скорости течения можно считать
сонаправленным (параллельным) во всех
точках рассматриваемого объёма жидкости.
Подъемная
сила
- составляющая
полной аэродинамической силы,
перпендикулярная вектору скорости
движения тела в потоке жидкости или
газа, возникающая в результате
несимметричности обтекания тела
потоком.
—
производная
скорости в направлении, перпендикулярном
направлению сдвига, с−1.Это
уравнение обычно используют при течении
жидкости в одном направлении, когда
вектор скорости течения можно считать
сонаправленным (параллельным) во всех
точках рассматриваемого объёма жидкости.
Подъемная
сила
- составляющая
полной аэродинамической силы,
перпендикулярная вектору скорости
движения тела в потоке жидкости или
газа, возникающая в результате
несимметричности обтекания тела
потоком.
Билет
№18Постулаты
СТО [править]В
первую очередь в СТО, как и в классической
механике, предполагается, что пространство
и время однородны,
а пространство также изотропно.
Если быть более точным (современный
подход) инерциальные системы отсчета
собственно и определяются как такие
системы отсчета, в которых пространство
однородно и изотропно, а время однородно.
По сути существование таких систем
отсчета постулируется.Постулат
1 (принцип
относительности Эйнштейна).
Любое физическое явление протекает
одинаково во всех инерциальных системах
отсчёта. Это означает, что форма зависимости
физических законов от пространственно-временных
координат должна быть одинаковой во
всех ИСО, то есть законы инвариантны
относительно переходов между ИСО.
Принцип относительности устанавливает
равноправие всех ИСО.Учитывая второй
закон Ньютона (или уравнения
Эйлера-Лагранжа в лагранжевой
механике)
можно утверждать, что если скорость
некоторого тела в данной ИСО постоянна
(ускорение равно нулю), то она должна
быть постоянна и во всех остальных ИСО.
Иногда это и принимают за определение
ИСО.Формально, принцип относительности
Эйнштейна распространил классический
принцип относительности (Галилея) с
механических на все физические явления.
Однако, если учесть, что во времена
Галилея физика заключалась собственно
в механике, то и классический принцип
тоже можно считать распространяющимся
на все физические явления. В том числе
он должен распространятся и на
электромагнитные явления, описываемые
уравнениями Максвелла. Однако, согласно
последним (и это можно считать эмпирически
установленным, так как уравнения выведены
из эмпирически выявленных закономерностей),
скорость распространения света является
определённой величиной, не зависящей
от скорости источника (по крайней мере
в одной системе отсчёта). Принцип
относительности в таком случае говорит,
что она не должна зависеть от скорости
источника во всех ИСО в силу их
равноправности. А значит, она должны
быть постоянной во всех ИСО. В этом
заключается суть второго постулата:Постулат
2 (принцип
постоянства скорости света).
Скорость света в «покоящейся» системе
отсчёта не зависит от скорости источника.
Поскольку источник имеет разные скорости
в разных ИСО, то это означает, что скорость
света одинакова во всех инерциальных
системах.Принцип
постоянства скорости света противоречит
классической механике, а конкретно -
закону сложения скоростей. При выводе
последнего используется только принцип
относительности Галилея и неявное
допущение одинаковости времени во всех
ИСО. Таким образом, из справедливости
второго постулата следует, что время
должно бытьотносительным -
неодинаковым в разных ИСО. Необходимым
образом отсюда следует и то, что
"расстояния" также должны быть
относительны. В самом деле, если свет
проходит расстояние между двумя точками
за некоторое время, а в другой системе
- за другое время и притом с той же
скоростью, то отсюда непосредственно
следует, что и расстояние в этой системе
должно отличаться.Необходимо отметить,
что световые сигналы, вообще говоря, не
требуются при обосновании СТО. Хотя
неинвариантность уравнений Максвелла
относительно преобразований
Галилеяпривела
к построению СТО, последняя имеет более
общий характер и применима ко всем видам
взаимодействий и физических
процессов. Фундаментальная
константа ![]() ,
возникающая в преобразованиях
Лоренца,
имеет смысл предельной скорости
движения материальных тел. Численно
она совпадает со скоростью света, однако
этот факт, согласно современной квантовой
теории поля (уравнения которой изначально
строятся как релятивистски инвариантные)
связан с безмассовостью электромагнитных
полей. Даже если бы фотонимел
отличную от нуля массу, преобразования
Лоренца от
этого бы не изменились. Поэтому имеет
смысл различать фундаментальную
скорость
и
скорость света
,
возникающая в преобразованиях
Лоренца,
имеет смысл предельной скорости
движения материальных тел. Численно
она совпадает со скоростью света, однако
этот факт, согласно современной квантовой
теории поля (уравнения которой изначально
строятся как релятивистски инвариантные)
связан с безмассовостью электромагнитных
полей. Даже если бы фотонимел
отличную от нуля массу, преобразования
Лоренца от
этого бы не изменились. Поэтому имеет
смысл различать фундаментальную
скорость
и
скорость света ![]() [8].
Первая константа отражает общие свойства
пространства и времени, тогда как вторая
связана со свойствами конкретного взаимодействия.В
связи с этим второй постулат следует
формулировать как существование
предельной (максимальной) скорости
движения.
По своей сути она должна быть одинаковой
во всех ИСО, хотя бы потому, что в противном
случае различные ИСО не будут равноправны,
что противоречит принципу относительности.
Более того, исходя из принципа
"минимальности" аксиом, можно
сформулировать второй постулат просто
как существование
некоторой скорости, одинаковой во всех
ИСО,
а после вывода соответствующих
преобразований - показать, что это
предельная скорость (потому, что
подстановка в эти формулы скоростей
больше этой скорости приводит к мнимости
координат)
Понятие одновременностиРассмотрим
теперь вопрос о сверке часов и об
одновременности событий в разных
системах отсчета с учетом постулатов
Эйнштейна.В механике Ньютона «истинный,
или стандартный, процесс течения
абсолютного времени не подвержен никаким
изменениям» и не зависит « от того,
быстры движения или медленны или их нет
вообще». Считалось, что такие понятия,
как «момент времени», «раньше», «позже»,
«одновременность», имеют сами по себе
смысл, правомерный для всей Вселенной,
и два каких-нибудь события, одновременные
для одной системы, одновременны и во
всех других системах. С точки зрения же
теории относительности Эйнштейна нет
такого понятия, как абсолютная
одновременность, как нет абсолютного
времени.Чтобы решить, одновременно ли
произошли в различных точках два события,
необходимо иметь в каждой из этих точек
точные часы, относительно которых можно
быть уверенным, что они идут синхронно.
Для этого можно перенести эти часы в
одну точку, отрегулировать их так, чтобы
они шли синхронно, и затем снова разнести
их по разным помещениям. Можно также
использовать сигналы времени. Позволяющие
сравнивать показания часов в различных
точках. На практике используют оба
способа. На корабле, например, есть
хронометр, который идет очень точно и
отрегулирован по контрольным часам в
порту отправления. Кроме того, для его
проверки во время плавания используются
сигналы точного времени по радио.Так
всеобщая абсолютная одновременность,
возможность которой подразумевалась
в классической физике, пропадает. Вместо
нее выходит на сцену относительная
одновременность событий, существующая
лишь для какого-то конкретного,
определенным образом движущегося
наблюдателя.Разные наблюдатели могут
устанавливать даже неодинаковую
очередность одних и тех же событий. Но
все это чрезвычайно тонко и возможно
отметить лишь при движении с гигантскими
относительными скоростями, сравнимыми
со скоростью света. Важно, чтобы
наблюдатели успевали заметно сместиться
за то крохотное время, пока световые
вспышки пробегают расстояние между
событиями.Таким образом, согласно теории
относительности в каждой из инерциальных
систем, находящихся в относительном
движении, существует собственное время
системы, которое показывают часы,
покоящиеся в этой системе. Следовательно,
при определении времени событий в
различных инерциальных системах события,
одновременные в одной системе, могут
оказаться неодновременными в другой
системе отсчета. Другими словами, не
существует абсолютной
одновременности.Преобразования
Лоренца −
преобразования координат и времени
какого-либо события при переходе от
одной инерциальной системы отсчёта к
другой. Инерциальная система отсчёта
– система отсчёта, движущаяся прямолинейно
с постоянной скоростью v. Преобразования
Лоренца отражают равноправие всех
инерциальных систем отсчёта в описании
законов природы. Если инерциальная
система отсчёта K' движется относительно
инерциальной системы отсчёта K с
постоянной скоростью v вдоль оси x, то
преобразования Лоренца имеют вид
[8].
Первая константа отражает общие свойства
пространства и времени, тогда как вторая
связана со свойствами конкретного взаимодействия.В
связи с этим второй постулат следует
формулировать как существование
предельной (максимальной) скорости
движения.
По своей сути она должна быть одинаковой
во всех ИСО, хотя бы потому, что в противном
случае различные ИСО не будут равноправны,
что противоречит принципу относительности.
Более того, исходя из принципа
"минимальности" аксиом, можно
сформулировать второй постулат просто
как существование
некоторой скорости, одинаковой во всех
ИСО,
а после вывода соответствующих
преобразований - показать, что это
предельная скорость (потому, что
подстановка в эти формулы скоростей
больше этой скорости приводит к мнимости
координат)
Понятие одновременностиРассмотрим
теперь вопрос о сверке часов и об
одновременности событий в разных
системах отсчета с учетом постулатов
Эйнштейна.В механике Ньютона «истинный,
или стандартный, процесс течения
абсолютного времени не подвержен никаким
изменениям» и не зависит « от того,
быстры движения или медленны или их нет
вообще». Считалось, что такие понятия,
как «момент времени», «раньше», «позже»,
«одновременность», имеют сами по себе
смысл, правомерный для всей Вселенной,
и два каких-нибудь события, одновременные
для одной системы, одновременны и во
всех других системах. С точки зрения же
теории относительности Эйнштейна нет
такого понятия, как абсолютная
одновременность, как нет абсолютного
времени.Чтобы решить, одновременно ли
произошли в различных точках два события,
необходимо иметь в каждой из этих точек
точные часы, относительно которых можно
быть уверенным, что они идут синхронно.
Для этого можно перенести эти часы в
одну точку, отрегулировать их так, чтобы
они шли синхронно, и затем снова разнести
их по разным помещениям. Можно также
использовать сигналы времени. Позволяющие
сравнивать показания часов в различных
точках. На практике используют оба
способа. На корабле, например, есть
хронометр, который идет очень точно и
отрегулирован по контрольным часам в
порту отправления. Кроме того, для его
проверки во время плавания используются
сигналы точного времени по радио.Так
всеобщая абсолютная одновременность,
возможность которой подразумевалась
в классической физике, пропадает. Вместо
нее выходит на сцену относительная
одновременность событий, существующая
лишь для какого-то конкретного,
определенным образом движущегося
наблюдателя.Разные наблюдатели могут
устанавливать даже неодинаковую
очередность одних и тех же событий. Но
все это чрезвычайно тонко и возможно
отметить лишь при движении с гигантскими
относительными скоростями, сравнимыми
со скоростью света. Важно, чтобы
наблюдатели успевали заметно сместиться
за то крохотное время, пока световые
вспышки пробегают расстояние между
событиями.Таким образом, согласно теории
относительности в каждой из инерциальных
систем, находящихся в относительном
движении, существует собственное время
системы, которое показывают часы,
покоящиеся в этой системе. Следовательно,
при определении времени событий в
различных инерциальных системах события,
одновременные в одной системе, могут
оказаться неодновременными в другой
системе отсчета. Другими словами, не
существует абсолютной
одновременности.Преобразования
Лоренца −
преобразования координат и времени
какого-либо события при переходе от
одной инерциальной системы отсчёта к
другой. Инерциальная система отсчёта
– система отсчёта, движущаяся прямолинейно
с постоянной скоростью v. Преобразования
Лоренца отражают равноправие всех
инерциальных систем отсчёта в описании
законов природы. Если инерциальная
система отсчёта K' движется относительно
инерциальной системы отсчёта K с
постоянной скоростью v вдоль оси x, то
преобразования Лоренца имеют вид
|
(1) |
c - скорость света в вакууме, β = v/c. Формулы, выражающие x', y', z', t' через x, y, z, t получаются из соотношения (1) заменой v на -v.
|
Следствия из преобразований ЛоренцаДлина движущегося стержня.Предположим, что стержень расположен вдоль оси х` в системе k` и движется вместе с системой k` со скоростью v.Разность между координатами конца и начала отрезка в системе отсчета, в которой он неподвижен, называется собственной длиной отрезка. В нашем случае l0 = х2` - х1`, где х2` - координата конца отрезка в системе k` и х/ - координата начала. Относительно системы k стержень движется. Длиной движущегося стержня принимают разность между координатами конца и начала стержня в один и тот же момент времени по часам системы k.
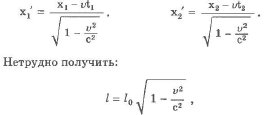
где l - длина движущегося стержня, l0 - собственная длина стержня. Длина движущегося стержня меньше собственной длины.
Темп хода движущихся часов.Пусть в точке х0` движущейся системы координат k` происходит последовательно два события в моменты t/ и t2. В неподвижной системе координат k эти события происходят в разных точках в моменты t1 и t2. Интервал времени между этими событиями в движущейся системе координат равен дельта t` = t2` - t1`, а в покоящейся дельта t = t2 - t1.На основании преобразования Лоренца получим:
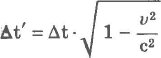 Интервал
времени дельта t` между событиями,
измеренный движущимися часами, меньше,
чем интервал времени дельта t между теми
же событиями, измеренный покоящимися
часами. Это означает, что темп хода
движущихся часов замедле относительно
неподвижных.Время, которое измеряется
по часам, связанным с движущейся точкой,
называется собственным
временем этой
точки.Относительность одновременности.
Интервал
времени дельта t` между событиями,
измеренный движущимися часами, меньше,
чем интервал времени дельта t между теми
же событиями, измеренный покоящимися
часами. Это означает, что темп хода
движущихся часов замедле относительно
неподвижных.Время, которое измеряется
по часам, связанным с движущейся точкой,
называется собственным
временем этой
точки.Относительность одновременности.
Из преобразований Лоренца следует, что если в системе k в точке с координатами x1 и х2 происходили два события одновременно (t1 = t2 = t0), то в системе k` интервал
![]()
понятие одновременности - понятие относительное. События, одновременные в одной системе координат, оказались неодновременными в другой.Относительность одновременности и причинность.Из относительности одновременности следует, что последовательность одних и тех же событий в различных системах координат различна.Не может ли случиться так, что в одной системе координат причина предшествует следствию, а в другой, наоборот, следствие предшествует причине?Чтобы причинно-следственная связь между событиями имела объективный характер и не зависела от системы координат, в которой она рассматривается, необходимо, чтобы никакие материальные воздействия, осуществляющие физическую связь событий, происходящих в различных точках, не могли передаваться со скоростью, большей скорости света.Таким образом, передача физического влияния из одной точки в другую не может происходить со скоростью, большей скорости света. При этом условии причинная связь событий носит абсолютный характер: не существует системы координат, в которой причина и следствие меняются местами.
19.Уравнение
состояния идельного гоза.Макроскопическими
системами называют
системы, содержащие большое количество
физических объектов.Термодинамические
макроскопические системы содержат
большое количество молекул (атомов,
ионов). Различают разные виды
термодинамических систем (ТС): закрытые,
открытые, адиабатные и изолированные
[1-5].Закрытые ТС это
системы, не обменивающиеся веществом
с другими системами.Открытые
ТС это
системы, обменивающиеся веществом и
энергией с другими системами.Адиабатные
ТС это
системы, в которых нет теплообмена с
другими системами.Изолированные
ТС это
системы, не обменивающиеся с другими
системами ни энергией, ни веществом.Идеальный
газ — математическая
модель газа,
в которой предполагается, что:
1) потенциальной
энергией взаимодействия молекул можно
пренебречь по сравнению с их кинетической
энергией;
2) суммарный объем молекул газа пренебрежимо
мал. Между молекулами не действуют силы
притяжения или отталкивания, соударения
частиц между собой и со стенками
сосуда абсолютно
упруги,
а время взаимодействия между молекулами
пренебрежимо мало по сравнению со
средним временем между столкновениями.
В расширенной модели идеального газа
частицы, из которого он состоит, имеют
также форму в виде упругих сфер или эллипсоидов,
что позволяет учитывать энергию не
только поступательного, но и
вращательно-колебательного движения,
а также не только центральные, но и
нецентральные столкновения частиц и
др.Уравнение
состояния идеального газа
![]()
![]() — давление,
— давление,![]() — молярный
объём,
— молярный
объём,![]() — универсальная
газовая постоянная
— универсальная
газовая постоянная![]() — абсолютная
температура,К.
Изопроцессы — термодинамические
процессы,
во время которых количество вещества
и ещё одна из физических величин —
параметров состояния: давление, объём или температура —
остаются неизменными. Так, неизменному
давлению соответствует изобарный
процесс,
объёму — изохорный,
температуре — изотермический, энтропии — изоэнтропийный (например,
обратимый адиабатический
процесс).
— абсолютная
температура,К.
Изопроцессы — термодинамические
процессы,
во время которых количество вещества
и ещё одна из физических величин —
параметров состояния: давление, объём или температура —
остаются неизменными. Так, неизменному
давлению соответствует изобарный
процесс,
объёму — изохорный,
температуре — изотермический, энтропии — изоэнтропийный (например,
обратимый адиабатический
процесс).
20.Распределение
молекул идеального газа по
скоростям.Термодинамика —
раздел физики, изучающий общие свойства
макроскопических систем, находящихся
в состоянии термодинамического
равновесия, и процессы перехода между
этими состояниями. Термодинамика не
исследует микропроцессы, лежащие в
основе этих превращений. Этим термодинамический
метод отличается
от статистического. Статисти́ческая
фи́зика —
это раздел теоретической
физики,
посвященный изучению систем с произвольным
(часто — бесконечным или несчетным
числом
степеней
свободы.
Изучаемые системы могут быть
как классическими,
так и квантовыми.
Статистическая физика описывает, как
из движений частиц системы складывается
усреднённая эволюция системы в
целомПло́тность
вероя́тности —
один из способов задания вероятностной
меры на евклидовом
пространстве ![]() .
В случае, когда вероятностная мера
является распределением
случайной величины,
говорят о плотности
случайной
величины.
Распределение молекул идеального газа
по скоростям выражается формулой
.
В случае, когда вероятностная мера
является распределением
случайной величины,
говорят о плотности
случайной
величины.
Распределение молекул идеального газа
по скоростям выражается формулой
![]() Наиболее вероятная скорость молекул
Наиболее вероятная скорость молекул
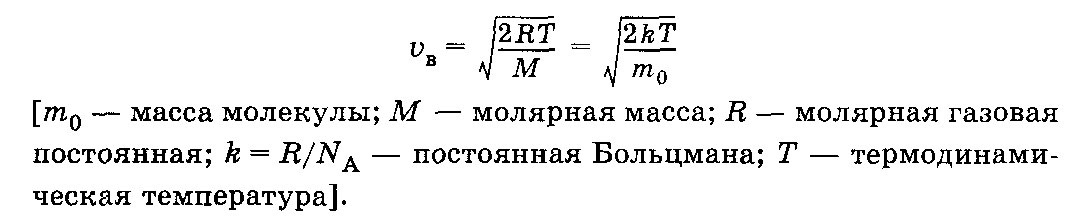 распределение
молекул идеального газа по энергиям
находится по формуле
распределение
молекул идеального газа по энергиям
находится по формуле
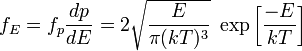 Барометрическая формула —
зависимость давления или плотности
газа от высоты в поле тяжести. Для идеального
газа,
имеющего постоянную температуру
и
находящегося в однородном поле тяжести
Барометрическая формула —
зависимость давления или плотности
газа от высоты в поле тяжести. Для идеального
газа,
имеющего постоянную температуру
и
находящегося в однородном поле тяжести
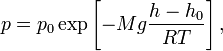 Распределение Больцмана – распределение
по энергиям частиц (атомов, молекул)
идеального газа в условиях термодинамического
равновесия. Закон распределения
Больцмана:
Распределение Больцмана – распределение
по энергиям частиц (атомов, молекул)
идеального газа в условиях термодинамического
равновесия. Закон распределения
Больцмана:
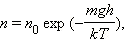 где
n
– концентрация молекул на высоте h,
n0
– концентрация молекул на начальном
уровне h
= 0,
где
n
– концентрация молекул на высоте h,
n0
– концентрация молекул на начальном
уровне h
= 0,
m – масса частиц, g – ускорение свободного падения, k – постоянная Больцмана, T – температура.
Распределение Максвелла-Больцмана:равновесное распределение частиц идеального газа по энергиям (E) во внешнем силовом поле (напр., в поле тяготения); определяется функцией распределения: f ~ e-E/kT где E - сумма кинетической и потенциальной энергий частицы, T - абсолютная температура, k - постоянная Больцмана
21.Основное
уравнение МКТ идеального газа.основное
уравнением молекулярно-кинетической
теории
![]() Средняя
кинетическая энергия поступательного
движения молекулы идеального газа зависит
только от его термодинамической
температуры Т и прямо пропорциональна
этой температуре.
Уравнение
среднеквадратичной скорости молекулы
Средняя
кинетическая энергия поступательного
движения молекулы идеального газа зависит
только от его термодинамической
температуры Т и прямо пропорциональна
этой температуре.
Уравнение
среднеквадратичной скорости молекулы
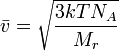 В статистической
физике температура
определяется как производная от энергии
системы по её энтропии:
В статистической
физике температура
определяется как производная от энергии
системы по её энтропии:
![]() где S — энтропия,
E — энергия термодинамической
системы.
где S — энтропия,
E — энергия термодинамической
системы.
Наиболее вероятная скорость молекул

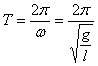 или
или 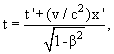
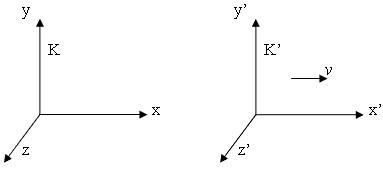 Рис.
Система координат K' движется относительно
неподвижной системы координат K со
скоростью v вдоль оси x.
Рис.
Система координат K' движется относительно
неподвижной системы координат K со
скоростью v вдоль оси x.