Билет 1.

Материальная точка и абсолютно твердое тело. Траектория, путь, перемещение, скорость, ускорение.

ускорение.Материальная точка - тело, размерами которого, в условиях данной задачи, можно принебреч.

Абсолютно твердое тело - тело, деформацией которого можно принебреч, в условиях данной задачи.

Система отсчета-совокупность тела осчета, связаное с ним системы координат и система отсчета времени по отношению к которому рассматривается движение мат. т. Кинематика материальной точки и поступательного движения твердого тела: ?движение в прямоугольной, криволинейной системе координаткак записать в разных системах координат через радиус вектор

Траектория - некоторая линия, описываемая движение мат. точки.

Путь - скалярная величина, характеризующая длинну траектории движения тела.

Перемещение - нравленный отрезок прямой, проведенный из начального положения движущейся точки в ее конечное положение (векторная величина)

Скорость: -векторная величина, характеризующая быстроту пермещения частицы по траектории, в который движется эта частица в каждый момент времени.-производная радиуса вектора частицы по времени.

-производная от перемещения по времени.

Ускорение:-векторная величина, характеризующая быстроту изменения вектора скорости.

-производная от скорости по времени.

Уравнение траектории – можно записать так: y=y(t), z=z(t), s=s(t).

Билет 2.Кинематика материальной точки.Скорость, ускорение.Тангенциальное, нормальное и полное

Тангенциальное ускорение — направлено по касательной к траектории. Является составляющей вектора ускорения a. Характеризует изменение скорости по модулю.

Центростремительное или Нормальное ускорение — возникает при движении точки по окружности. Является составляющей вектора ускорения a. Вектор нормального ускорения всегда направлен к центру окружности.

Полное ускорекние - это корень квадатный из суммы квадратов нормально и тангенцального ускорений.

Принцип относительности – фундаментальный физ. Принцип, один из принципов симетрии, согласно которому все физ. Процессы в инерциальных сист. Отсчета протекают одинакого, независимо от того, неподвижна ли система или она назодится в состоянии равномерного и прямолинейного движения.Суперпозиция движения – результат воздействия на частицу нескольких внешн. сил, есть векторная сумма воздействия этих сил.

Билет3 3Кинематика вращательного движения материальной точки. Угловые величины. Связь между угловыми и линейными величинами.Угловое перемещение - векторная величина, характеризующая изменение угловой координаты в процессе ее движения.

Угловая скорость - отношение угла поворота радиус-вектора точки к промежутку времени, за который произошел этот поворот.(направление вдоль оси вокруг которой вращается тело)

Частота вращения - физическая величина, измеряемая числом полных оборотов, совершаемых точкой в единицу времени при равномерном движении в одном направлении(n)Период вращения - промежуток времени, в течение которого точка совершает полный оборот, двигаясь

по окружности (T)N – число оборотов,совершаемых телом за время t.

Угловое ускорение - величина харатеризующая изменение вектора угловой скорости со временем.

Связь между угловыми и линейными величинами:

связь между линейной и угловой скоростью.

связь между тангенциальным и угловым ускорением.

вязь между нормальным (центростремительным) ускорением, угловой скоростью и линейной скоростью.Уравнение зависимости угла поворота от времени:dᵩ=ὼdt

Билет 4.Динамика материальной точки. Классическая механика, границы ее применимости. Законы Ньютона. Инерциальные системы отсчета.

Первый закон Ньютона (закон инерции):Существуют такие системы отсчёта, относительно которых материальная точка при отсутствии внешних воздействий находится в состоянии покоя или движется равномерно и прямолинейно .Причины изменения скорости – В результате воздействия силы либо несолько сил нескомпенсированы.Инерциальная система отсчета - система отсчёта, в которой справедлив закон инерции: любое тело, на которое не действуют внешние силы или действие этих сил компенсируется, находится в состоянии покоя или равномерного прямолинейного движения.Неинерциальные сист. отсчета – не действует 1-ый закон ньютона; всякаяя система отсчета движущаяся с ускорением или поворачивающаяся относительно инерциальной сист. Принцип относительности Галилея – законы механики во всех инерционных сист. одинаковы.Преобразования Галилея: x’=x-Vt; y’=y; z’=z; t’=t.Масса - количесенная характеристика инертности.

Сила – векторная величина, которая являестя мерой мех. воздействия на тело со стороны других тел или полей, в результате чего преобретают ускорение или деформируются.И мпульс тела – количество движения P: P=mv.

Второй закон Ньютона:В инерциальной системе отсчета произведение массы тела на его ускорение равное действующей на тело силе.

a=(сумма всех сил)F_i/mТретий закон Ньютона:

Силы, с которыми действуют друг на друга взаимодействующие тела, равны по модулю и противоположы по напрвлению.

И нвариантность уравнения движения относительно преобразования галилея - физ. величины, не изменяющиеся при переходе от одной инерциальной системы к другой наз. инвареантными. l’=x₂’-x₁’=x₂-x₁ l’=l

Δt’=t₂’-t₁’=t₂-t₁ Δt’=Δt – Следовательно, отрезки длин l и интервалы времени Δt являются инвариантами ньютоновсой классической механики. invarians – неизменный.

Билет №5.

Классификация сил в природе – влияние одного тела (поля) на другое, вызывающее ускорение (это сила).

- гравитационная, - электромаггнитные, -сильные(ответтвенные за связь частиц в ядрах), -слабые(ответственные за распад частиц).

Закн Всемирного тяготения – силы с которой два тела притягив. друг к другу наз. гравитационной силой(СИЛОЙ ТЯГОТЕНИЯ).F=Y*m₁m₂/r².

Физический смысл гравитационной постоянной состоит в том, что она равна силе G=6,67*10-11H м²/кг², с которой взаимодействуют два тела массами по й кг, которые находятся на расстоянии 1 м друг от друга.

Сила тяжести – сила, с которой тело притягивается к земле под действием поля тяготения земли F_т=G M m/r²

Вес тела – сила, в которой в следствие притяжения к хемле тело действует на вою опору или подвес P=F_т=mg.

Упругие силы – возникают при деформации тела и направлены в сторону обратную смещению.

Закон Гука - относительная деформация ε пропорциональна напряжению σ, где Е- модуль Юнга.

F_x=-kx- для малых деформаций. Уравнение теории упругости, связывающее напряжение и деформацию упругой среды.

Сила трения – один из видов взаимодействия тел, возникает при взаимодействии двух тел.

Сила сопротивления – сила трения покоя.

С ложение сил – нахождение равнодействующей нескольких сил.R= F₁²+ F₂²+2F₁F₂cosα, модуль равнодействузей силы (нахождение).

билет №6 Неинерциальные системы отсчета – это система отсчета,в которой наблюдается ускорение движения тел при отсутствии действия на них сил со стороны других тел Силы инерции – силы обусловленные ускоренным движением неинерциальной системы отсчета относительно инерциальной системы отсчета Сила Кореолиса – одна из сил инерции, существующая в неинерциальной системе отсчета из за вращения и законов инерции, проявляющаяся при движении в направлении под углом оси вращения.

Уравнение движения в неинерциальных системах отсчета , где   — масса тела,  ,   — ускорение и скорость тела относительно неинерциальной системы отсчёта,   — сумма всех внешних сил, действующих на тело,   — переносное ускорение тела,   — кориолисово ускорение тела,   — угловая скорость вращательного движения неинерциальной системы отсчёта вокруг мгновенной оси, проходящей через начало координат,   — скорость движения начала координат неинерциальной системы отсчёта относительно какой-либо инерциальной системы отсчёта.

Принцип эквивалентности- утверждение согласно которому поле тяготения в небольшой области пространства и времени по своему проявлению тождественно ускоренной системе отсчета.

Границы применимости Ньютоновской механики- она объясняет множество физич. явлений и процессов в земных и внезимных условиях, составляет основу для многих технических достижений. На ее фундаменте формировались многие методы научных иследований в различных отрослях.

Билет№ 7 Механическая система и ее состояние- совокупность множества материальных частиц образуют систему материальных точек. Если система материальных частиц такова , что движение каждой ее точки зависит от положения остальных ее точек, то она назыв. механич. системой. Независимые координаты и скорости (или импульсы) системы в произвольный момент времени, определяют механическое состояние системы.

Внутренние силы- назыв. силы взаимодействия между отдельными точками системы(F_i)

Внешние силы- это силы действующие на движущуюся механическую систему извне и ей не принадлежит (F_e).

Замкнутая система – представляет собой систему, в которой отсутствует обмен веществом и энергии и информации с внешней средой или окружением.

Импульс системы – N материальных точек называется векторная сумма ипульсов отдельных материальных точек образующих данную систему: P=(сумма импульсов)m_kv_k

Закон сохранения импульсов – любые силы действующие внутризамкнутой системы мат. точек, не могут изменить состояние центра масс системы(его покоя или равномерного прямолинейного движения)(P₁’)+(P₂’)=(P₁)+(P₂) –закон сохранения импульсов для двух тел.

Центр масс – точка, характеризующая распределение масс в теле или механической системе.

Способ нахождения: R_ц.м.=(сумма)m_ir_i/(сумма)m_i Уравнение движения центр масс - Положение центра масс определяется его радиус-вектором 

Реактивное движение – движение тела, возникающее при отделении некоторой его части с определенной скоростью относительно тела, например при истечении продуктв сгорания из сопла реактивного летательного аппарата.

Уравнение Мещерского -

где:  — масса материальной точки переменной массы, изменяющаяся за счет обмена частицами с окружающей средой;  — скорость движения материальной точки переменной массы;

 — внешние силы, действующие на материальную точку переменной массы со стороны её внешнего окружения (в том числе, если такое имеет место, и со стороны среды, с которой она обменивается частицами, например электромагнитные силы — в случае массообмена с магнитной средой, сопротивление среды движению и т. п.);  — относительная скорость присоединяющихся частиц;  — относительная скорость отделяющихся частиц;

Формула Циалковсого:  — масса материальной точки переменной массы, изменяющаяся за счет обмена частицами с окружающей средой;  — скорость движения материальной точки переменной массы;

•  — внешние силы, действующие на материальную точку переменной массы со стороны её внешнего окружения (в том числе, если такое имеет место, и со стороны среды, с которой она обменивается частицами, например электромагнитные силы — в случае массообмена с магнитной средой, сопротивление среды движению и т. п.);

•  — относительная скорость присоединяющихся частиц;

•  — относительная скорость отделяющихся частиц;

Билет 5. Центр масс (инерции) тела. Импульс материальной точки и твердого тела. Закон сохранения импульса. Движение центра масс.

Центр масс системы материальный точек - точка, положения которой характеризует распеределение массы системы в пространстве.

распеределение масс в системе координат.

Положение центра масс тела зависит от того, как распределяется по обьему тела его масса.

Движение центра масс определяется только внешними силами, действующими на систему.Внутрение силы системы не влияют на положение центра масс.

положение центра масс.

Центр масс замкнутой системы движется прямолинейна и равномерно или остается неподвижным.

Импульс материальной точки - векторная величина равная произведению массы точки на ее скорость.

Импульс тела равен сумме импульсов его отдельных элементов.

Изменение импульса мат. точки пропорционален приложеной силе и имеет такое же направление, как и сила.

Импульс системы мат. точек могут изменить только внешние силы, причем изменение импульса системы пропорционально сумме внешних сил и совпадает с ней по направлению.Внутрение силы, изменяя импульсы отдельных тел системы, не изменяют сумарный импульс системы.

Закон сохранения импульса: если сумма внешних сил, действующих на тело системы, равна нулю, то импульс системы сохраняется.

Билет 8. Работа силы. Энергия. Мощность. Кинетическая и потенциальная энергия. Силы в природе.

Работа - физическая величина, характеризуюая результат действия силы и числено равная скалярному произведнию вектора силы и вектора перемещения, совершенно под действием этой силы.

A = F · S ·cosа (а-угол между направлением силы и направлением перемещения)Джоуль

Мощность- физическая величина, характеризующаяскорость совершения работы и числено равная отношению работы к интервалу, за который работа совершена.

средняя мощность; мгновенная мощность.Ватт

Работа силы тяжести:

Работа силы упругости:

работа, совершаемая силой упругости при изменении деформации пружины от некоторого начального значения x1 до конечного значения x2

Работа силы трения:Сила трения возникает при посредственном соприкосновении тел и всегда направлена вдоль поверхности соприкосновения.

Если сила не достаточно велика, то тело остаётся в покое, следовательно на него действует сила равная по модулю силе тяги и направленна в противоположную ей сторону – это и есть сила трения покоя. Fтр=MN

M- коэффициент  трения.Если сила тяги больше силы трения, тело получает ускорение и двигается с места.Сила трения скольжения всегда направлена противоположно скорости движения тела.Полная механическая энергия системы - энергия механического движения и взаимодействия:  E=T+P  т. е. равна сумме кинетической и потенциальной энергий.

Механическая энергия - это величина характеризующая движение и взаимодействие тел и являющаяся функцией скоростей и взаимного расположения тел.  Механическая энергия — это энергия, связанная с движением объекта или его положением, способность совершать механическую работу.

Закон сохранения механической энергии:Если в замкнутой системе не действуют силы, трения и силы сопротивления, то сумма кинетической и потенциальной энергии всех тел системы остается величиной постоянной.

Энергией - это скалярная физическая величина, являющаяся единой мерой различных форм движения материи и мерой перехода движения материи из одних форм в другие.Физическая величина, равная половине произведения массы тела на квадрат его скорости, называется кинетической энергией тела.Кинетическая энергия-энергия движения.

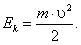
A = Ek2 – Ek1

Физическую величину, равную произведению массы тела на модуль ускорения свободного падения и на высоту, на которую поднято тело над поверхностью Земли, называют потенциальной энергией взаимодействия тела и Земли.

Потенциальная энергия-энергия взаимодействия.

Ep = m∙g∙h.

А= – (Ер2 – Ер1).

Билет 7.

Консервативные и диссипативные силы. Закон сохранения механичсекой энергии. Условие равновесия механической системы.

Консервати́вные си́лы (потенциальные силы) — силы, работа которых не зависит от формы траектории (зависит только от начальной и конечной точки приложения сил) Консервативные силы — такие силы, работа по любой замкнутой траектории которых равна 0.

работа консервативных сил по произвольному замкнутому контуру равна 0;

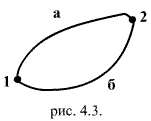
Силу , действующую на материальную точку, называют консервативной или потенциальной, если работа , совершаемая этой силой при перемещении этой точки из произвольного положения 1 в другое 2, не зависит от того, по какой траектории это перемещение произошло:

Изменение направления движения точки вдоль траектории на противоположное вызывает изменение знака консервативной силы, так как величина меняет знак. Поэтому при перемещении материальной точки вдоль замкнутой траектории , например , работа консервативной силы равна нулю .

Примером консервативных сил могут служить силы всемирного тяготения, силы упругости, силы электростатического взаимодействия заряженных тел. Поле, работа сил которого по перемещению материальной точки вдоль произвольной замкнутой траектории равна нулю, называется потенциальным.

Диссипативные силы - силы, при действии которых на движущуюся механическую систему её полная механическая энергия убывает, переходя в другие, немеханические формы энергии, например в теплоту.

пример диссипативных сил: сила вязкого или сухого трения.

Закон сохранения механичсекой энергии:

Сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему и взаимодействующих между собой посредством сил тяготения и сил упругости, остается неизменной.

Ek1 + Ep1 = Ek2 + Ep2

Замкнутая система- это система, на которую не действуют внешнии силы или из действие скомпенсировано.

Условие равновесия механической системы:

Статика - раздел механики, изучающмй условия равновесия тел.

Чтобы невращающееся тело находилось в равновесии, необходимо, чтобы равнодействующая всех сил, приложенных к телу, была равна нулю.

Если тело может вращаться относительно некоторой оси, то для его равновесия недостаточно равенства нулю равнодействующей всех сил.

Правило моментов: тело, имеющее неподвижную ось вращения, находится в равновесии, если алгебраическая сумма моментов всех приложенных к телу сил относительно этой оси равна нулю: M1 + M2 + ... = 0.

Длина перпендикуляра, проведенного от оси вращения до линии действия силы, называется плечом силы.

Произведение модуля силы F на плечо d называется моментом силы M. Положительными считаются моменты тех сил, которые стремятся повернуть тело против часовой стрелки.

Билет 8.Кинематика вращательно движения твердого тела. Угловое перемещение, угловая скорость, угловое ускорение. Связь между линейными и угловыми характеристиками. Кинетическая энергия вращательного движения.

+Билет 3.

Для кинематического описания вращения твердого тела удобно использовать угловые величины: угловое перемещение Δφ, угловую скорость ω

В этих формулах углы выражаются в радианах. При вращении твердого тела относительно неподвижной оси все его точки движутся с одинаковыми угловыми скоростями и одинаковыми угловыми ускорениями. За положительное направление вращения обычно принимают направление против часовой стрелки.

Вращательно движение твердого тела :

1) вокруг оси - движение, при котором все точки тела, лежащие на оси вращения, неподвижны, а остальные точки тела описывают окружности с центрами на оси;2) вокруг точки - движение тела, при котором одна его точка О неподвижна, а все другие движутся по поверхностям сфер с центром в точке О.

Кинетическая энергия вращательного движения.

Кинетическая энергия вращательного движения – энергия тела связанная с его вращением.

Разобьем вращающееся тело на малые элементы Δmi. Расстояния до оси вращения обозначим через ri, модули линейных скоростей – через υi. Тогда кинетическую энергию вращающегося тела можно записать в виде:

Физическая величина зависит от распределения масс вращающегося тела относительно оси вращения. Она называется моментом инерции I тела относительно данной оси:

В пределе при Δm → 0 эта сумма переходит в интеграл.

Таким образом, кинетическую энергию твердого тела, вращающегося относительно неподвижной оси, можно представить в виде:

Кинетическая энергия вращательного движения определяется моментом инерции тела относительно оси вращения и его угловой скоростью.

Билет 9.

Динамика вращательного движения. Момент силы. Момент инерции. Теорема Штейнера.

Момент силы - величина, характеризующая вращательный эффект силы при действии её на твёрдое тело. Различают Момент силы относительно центра (точки) и относительно оси.

1.Момент силы относительно центра О величина векторная. Его модуль Mo = Fh, где F - модуль силы, a h - плечо (длина перпендикуляра, опущенного из О на линию действия силы)

С помощью векторного произведения момент силы выражается равенством Mo = [rF], где r - радиус-вектор, проведённый из О в точку приложения силы.

2.Момент силы относительно оси величина алгебраическая, равная проекции на эту ось.

Момент силы (крутящий момент; вращательный момент; вращающий момент) — векторная физическая величина, равная произведению радиус-вектора, проведенного от оси вращения к точке приложения силы, на вектор этой силы.

это выражение является вторым законом Ньютона для вращательного движения.

Оно справедливо только тогда: а) если под моментом М понимают часть момента внешней силы, под действием которой происходит вращение тела вокруг оси - это тангенциальная составляющая. б) нормальная составляющая из момента силы не участвует во вращательном движении, так как Mn старается сместить точку с траектории, и по определению тождественно равна 0, при r- const Mn=0, а Mz - определяет силу давления на подшипники.

Момент импульса - физическая величина, зависящая от того сколько массы вращается и как она распределена относительно оси вращения и с какой скоростью происходит вращение.

Момент импульса относительно точки — это псевдовектор.

Момент импульса относительно оси — скалярная величина.

Момент импульса L частицы относительно некоторого начала отсчёта определяется векторным произведением ее радиус-вектора и импульса: L=[rP]

r - радиус-вектор частицы относительно выбранного неподвижного в данной системе отсчета начала отсчёта.

P - импульс частицы.

L = rp sinА = p l;

 Пара сил - две равные по величине и противоположные по направлению силы, приложенные к одному телу. Равнодействующая пары сил — нулевой вектор. Кратчайшее расстояние между линиями действия сил, образующих пару сил, называют плечом пары.

Моментом пары наз. величина, равная взятому с соотв. знаком произведению модуля одной из сил пары на ее плечо (Понятие момента силы связано с точкой, относительно к-рой берется момент. Момент пары определяется только ее моментом и плечом; ни с какой точкой плоскости эта величина не связана). Св-ва : сумма моментов сил пары относительно точки не зависит от выбора точки и всегда равняется моменту пары, пара сил не имеет равнодействующей - нельзя уравновесить одной силой.скорость изменения момента импульса системы равна векторной сумме моментов внешних сил M, действующих на части этой системы.

                                     dL/dt = M.

Закон сохранения импульса - момент импульса системы тел сохраняется неизменным при любых взаимодействиях внутри системы, если результирующий момент внешних сил, действующих на нее, равен нулю.

Билет№10Момент импульса относительно оси — скалярная величина.

Для систем, совершающих вращение вокруг одной из осей симметрии (вообще говоря, вокруг так называемых главных осей инерции), справедливо соотношение:

момент импульса тела относительно оси вращения.Момент импульса твердого тела относительно оси есть сумма моментов импульса отдельных частей.Момент инерции - скалярная физическая величина, мера инертности тела во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении.Момент инерции зависит от массы тела и от расположения частиц тела относительно оси вращения. Теорема Штейнера;.

Момент инерции данного тела относительно, какой либо данной оси зависит не только от массы, формы и размеров тела, но также от положения тела по отношению к этой оси.

Согласно теореме Гюйгенса - Штейнера - момент инерции тела J относительно произвольной оси равен сумме:

1)момента инерции этого тела Jо, относительно оси, проходящий через центр масс этого тела, и параллельной рассматриваемой оси,

2) произведения массы тела на квадрат расстояния между осями.

Уравнение динамики твердого тела вращающегося вокруг неподвижной оси - Момент инерции системы материальных точек относительно оси вращения равен сумме произведений масс материальных точек системы на квадраты их расстояний до оси вращения:

Кинетическая энергия вращательного движения — энергия тела, связанная с его вращением.Основные кинематические характеристики вращательного движения тела — его угловая скорость ( ) и угловое ускорение. Основные динамические характеристики вращательного движения — момент импульса относительно оси вращения z:

и кинетическая энергия

где I_z — момент инерции тела относительно оси вращения.

Работа внешних сил при вращении твердого тела -  работа при вращении тела  равна произведению момента действующей силы на угол поворот

Билет №11

Момент инерции сложных тел - Момент инерции сложной фигуры равен сумме моментов инерции ее составных частей  Это непостредственно следует из свойств определенного инетеграла  где А = А1 + А2 + ...

Таким образом, для вычисления момента инерции сложной фигуры надо разбить ее на ряд простых фигур, вычислить моменты инерции этих фигур и затем просуммировать эти моменты инерции.Понятие о степени свободы твердых тел - Числом степеней свободы твердого тела называется число независимых параметров, которые однозначно определяют положение тела в пространстве относительно рассматриваемой системы отсчета. Движение твердого тела во многом зависит от числа его степеней свободы.Вращение тела относительно свободной оси Для того чтобы сохранить положение оси вращения твердого тела с течением време­ни неизменным, используют подшипники, в которых она удерживается. Однако существуют такие оси вращения тел, кото­рые не изменяют своей ориентации в про­странстве без действия на нее внешних сил. Эти оси называются свободными ося­ми (или осями свободного вращения). Можно доказать, что в любом теле су­ществуют три взаимно перпендикулярные оси, проходящие через центр масс тела, которые могут служить свободными осями (они называются главными осями инерции тела). Например, главные оси инерции однородного прямоугольного параллеле­пипеда проходят через центры противопо­ложных граней (рис. 30). Для однородно­го цилиндра одной из главных осей инер­ции является его геометрическая ось, а в качестве остальных осей могут быть две любые взаимно перпендикулярные оси, проведенные через центр масс в плоско­сти, перпендикулярной геометрической оси цилиндра. Главными осями инерции шараявляются любые три взаимно перпендику­лярные оси, проходящие через центр масс.Для устойчивости вращения большое значение имеет, какая именно из свобод­ных осей служит осью вращения.Можно показать, что вращение во­круг главных осей с наибольшим и наи­меньшим моментами инерции оказывается устойчивым, а вращение около оси со средним моментом — неустойчивым. Так, если подбросить тело, имеющее форму параллелепипеда, приведя его одновре­менно во вращение, то оно, падая, будет устойчиво вращаться вокруг осей 1 и 2(рис. 30).Если, например, палочку подвесить за один конец нити, а другой конец, закреп­ленный к шпинделю центробежной маши­ны, привести в быстрое вращение, то па­лочка будет вращаться в горизонтальной плоскости около вертикальной оси, пер­пендикулярной оси палочки и проходящей через ее середину (рис.31). Это и есть свободная ось вращения (момент инерции при этом положении палочки максималь­ный). Если теперь палочку, вращающуюся вокруг свободной оси, освободить от внеш­них связей (аккуратно снять верхний ко­нец нити с крючка шпинделя), то положе­ние оси вращения в пространстве в тече­ние некоторого времени сохраняется. Свойство свободных осей сохранять свое положение в пространстве широко при­меняется в технике. Вращение тела относительно указанной точки - Моментом инерции материальной точки относительно оси вращения называется физическая величина, численно равная произведению массы точки на квадрат расстояния точки до оси вращения (Рисунок 10).I = mr² Момент инерции - величина скалярная.Моментом инерции механической системы относительно неподвижной оси называется физическая величина, равная сумме произведений масс всех точек системы на квадраты их расстояний до оси вращения.

I =   m_i∙ r_i²

Гироскопический эффект - Гироскопическим эффектом называется явление сохранения неизменности своего направления в пространстве быстровращающимся осесимметричным твердым телом.Гироскопический эффект свойственен небесным телам, артиллерийским снарядам, роторам турбин, устанавливаемых на судах, винтам самолетов и т.п.Для обеспечение свободного вращения гироскопического тела (гироскопа) в пространстве его обычно закрепляют на кольцах так называемого карданного подвеса (рис. 1) в котором оси внутренних и внешних колец и ось гироскопа пересекаются в одной точке, называемой центром подвеса.Прецессия гироскопа - называется движение по окружности конца оси гироскопа относительно некоторой оси, сориентированной вдоль вектора внешней силы, происходящее под действием этой силы. Вычислим угловую скорость прецессии гироскопа _п, ось которого смещена относительно горизонтальной плоскости на угол . Прецессия обусловлена действием внешней силы F, создающей момент M._п = d/dt;

d = dL/(L·cos()) = M·dt/(L·cos());  _п = M/(L·cos()) = M/(I··cos()),                           где L·cos() - проекция момента импульса на плоскость вращения гироскопа (плоскость, в которой располагаются вектора dL).

Билет №12

Колебательные движения тела – это движения, повторяющиеся через определенный промежуток времени.

Условия возникновения механических колебаний 1. Хотя бы одна сила должна зависеть от координат. 2. При выведении тела из положения устойчивого равновесия возникает равнодействующая, направленная к положению равновесия. С энергетической точки зрения это значит, что возникают условия для постоянного перехода кинетической энергии в потенциальную и обратно. 3. Силы трения в системе малы.
Для возникновения колебания тело необходимо вывести из положения равновесия, сообщив либо кинетическую энергию (удар, толчок), либо – потенциальную (отклонение тела).

Уравнение гармонического колебания — колебания, при которых физическая (или любая другая) величина изменяется с течением времени по синусоидальному или косинусоидальному закону. Кинематическое уравнение гармонических колебаний имеет вид

или

,

Амплитуда – это наибольшее отклонение колеблющегося тела от положения равновесия.

Измеряется в метрах, сантиметрах и т.п.

Частота колебаний – это число колебаний, совершаемых в единицу времени. За единицу частоты принято одно колебание в секунду. Название этой единицы – герц (Гц).

Частота колебаний обозначается буквой ν («ню»).

Период колебаний – это промежуток времени, в течение которого тело совершает одно полное колебание.

Период колебаний обычно измеряется в секундах.Обозначается буквой Т.Фаза колебаний — это величина, которая определяет положение колебательной системы в любой момент времени. Обозначается φ. Измеряется в радианах.Если колебания происходят по закону синуса и косинуса, т. е. при гармонических колебаниях, то фаза колебаний является аргументом функции cos (ωt +φ_o), где ω — циклическая частота колебаний,t — время,φ_o — начальная фаза колебаний, т. е. фаза в начальный момент времени.

Скорость и ускорение м. т. при гармонических колебаниях - Найдем, как зависит от времени скорость и ускорение тела, совершающего гармонические колебания по закону x = x_maxcosωt. (3)  вдоль координатной оси OX. Скорость υ_x движения тела определяется выражением υ_x = ∆ x/∆t.   Более строго проекция скорости поступательного движения тела на ось ОХ определяется как производная координаты x по времени: υ_x = x’(t) = – x_maxωsinωt = x_maxωcos(ωt+π/2) (4)   Для определения проекции ускорения движения тела в любой момент времени необходимо найти производную от проекции скорости υ_x по времени t: a_x = υ_x’(t) = – x_maxω²cosωt = x_max ω²cos(ωt+π) (5) Дифференциальное уравнение гармонических колебаний - Обобщенное гармоническое колебание в дифференциальном виде

Билет №13

Квазиупругая сила, направленная к центру О сила F, величина которой пропорциональна расстоянию rот центра О до точки приложения силы; численно F = cr, где с — постоянный коэффициент. Тело, находящееся под действием К. с., обладает потенциальной энергией П = ¹/₂cr². Название "К. с." связано с тем, что аналогичным свойством обладают силы, возникающие при малых деформациях упругих тел (так называемые силы упругости). Для материальной точки, находящейся под действием К. с., центр О является положением устойчивого равновесия. Выведенная из этого положения точка будет совершать около О линейные гармонические колебания или описывать эллипс (в частности, окружность).