
- •Лекция №6 расчет прочности изгибаемых элементов
- •§ 4.1. Виды изгибаемых элементов и их конструктивные особенности
- •Ненапрягаемая продольная арматура
- •Расчет прочности по нормальным сечениям
- •§ 4.3. Расчет прочности по наклонным сечениям
- •Расчет элементов прямоугольного сечения на действие изгибающего момента по наклонной трещине.
Расчет элементов прямоугольного сечения на действие изгибающего момента по наклонной трещине.
Расчет наклонных сечений на действие изгибающего момента заключается в проверке их прочности при известном количестве и расположении продольной арматуры, определенных из расчета прочности по нормальным сечениям. Прочность сечения будет обеспечена, если расчетный момент внешних сил М0 относительно точки О (приложения равнодействующей усилий в сжатой зоне) не превысит суммы моментов расчетных усилий в продольной арматуре, хомутах и отогнутых стержнях относительно той же точки (см. рис. 4.7):
![]() ,
(4.45)
,
(4.45)
г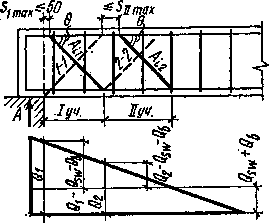 де
де
![]() ,
,
![]() ,
,
![]() —
расстояния от центров тяжести сечений
соответственно продольной арматуры,
хомутов и отгибов
до моментной точки А.
—
расстояния от центров тяжести сечений
соответственно продольной арматуры,
хомутов и отгибов
до моментной точки А.
При
этом высоту сжатой зоны
бетона определяют из условий
равновесия проекций
усилии в бетоне и арматуре
в рассматриваемом сечении
на продольную ось элемента.
Поскольку, напряжение
в продольной арматуре
у торцов элементов возрастает
от нуля у начала стержня
до
в конце зоны анкеровки (см. § 3.3), вводимое
в расчет сопротивление
арматуры умножают на коэффициент
условий работы,
численно равный отношению
![]() .
.
На действие изгибающего момента рассчитывают наклонные сечения, которые проходят через ослабленные участки элемента: в местах обрыва или отгиба продольной арматуры в пролете, у грани крайней свободной опоры балок и у свободного конца консолей при отсутствии у продольной арматуры специальных анкеров, а также в местах резкого изменения конфигурации элементов.
В
целях экономии металла часть продольной
арматуры
(до 50 % максимальной расчетной площади)
может не
доводиться до опоры и обрываться в
пролете там, где она
не требуется по расчету. В этом случае
растянутые стержни
должны заводиться за точку теоретического
обрыва
(т.е. за сечение 1-1,
в
котором эти стержни не требуются по
расчету) на длину не менее
![]() (
(![]() —
диаметр обрываемого стержня) и не
менее
,
на протяжении которой в наклонных
сечениях (3
—
3)
отсутствие
обрываемых
стержней компенсируется поперечной
арматурой:
—
диаметр обрываемого стержня) и не
менее
,
на протяжении которой в наклонных
сечениях (3
—
3)
отсутствие
обрываемых
стержней компенсируется поперечной
арматурой:![]() , (4.46)
, (4.46)
где
![]() —
расчетная поперечная сила и усилие,
воспринимаемое
поперечными стержнями в месте
теоретического
обрыва;
—
расчетная поперечная сила и усилие,
воспринимаемое
поперечными стержнями в месте
теоретического
обрыва;
![]() —
расстояние, на котором обрываемый
стержень включается в работу, начиная
с сечения 2
—
2
(рис. 4.9, б).
—
расстояние, на котором обрываемый
стержень включается в работу, начиная
с сечения 2
—
2
(рис. 4.9, б).
Места
теоретического обрыва
стержней устанавливают
графоаналитическим способом. С этой
целью на эпюру
изгибающих моментов от внешней нагрузки
(рис.
4.9, в)
наносят
в том же масштабе эпюру моментов,
воспринимаемых
сечением элемента с фактически имеющейся
растянутой арматурой. Пусть, например,
в балке по наибольшему
моменту подобрана арматура из четырех
стержней
1, 2, 3, 4
(рис.
4.9, б).
Два из, них 1, 2
доводят
до опоры, стержни 3,
4
обрывают
в пролете. Для определения
места их теоретического обрыва на
графике (рис.
4.9, в) в принятом масштабе откладывают
момент, воспринимаемый
сечением, армированным стержнями 1,
2
с
площадью
![]() и
проводят
и
проводят
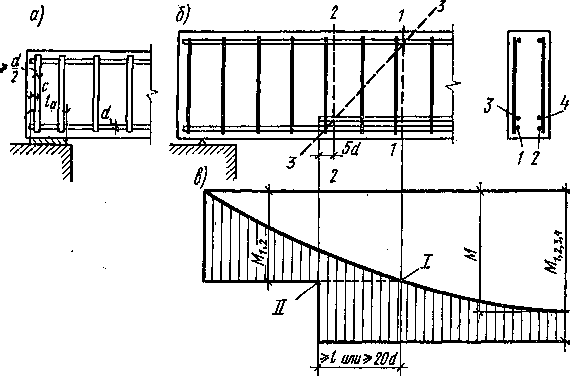
Рис. 4.9. Обеспечение анкеровки арматуры на опоре (а) и в пролете (б); построение эпюры арматуры (в):
I — место теоретического обрыва продольных стержней; II — то же, фактического
горизонтальную линию, параллельную оси. Место пересечения этой линии с эпюрой изгибающих моментов (сечение II) и будет местом теоретического обрыва.
■ Расчет элементов без поперечной арматуры.
В
некоторых типах железобетонных
конструкций (сплошных
плитах, балках высотой до 15 см,
многопустотных сборных
плитах высотой
![]() см
и т.п.) допускается не
устанавливать поперечную арматуру. В
этом случае расчет
прочности по наклонным сечениям
производят по уравнению
(4.34) при
см
и т.п.) допускается не
устанавливать поперечную арматуру. В
этом случае расчет
прочности по наклонным сечениям
производят по уравнению
(4.34) при
![]() .
.
С учетом опытных данных условия прочности будут иметь вид
![]() , (4.47)
, (4.47)
но
не более
![]() и
не менее
,
где
и
не менее
,
где
![]() — поперечная сила в наклонном сечении;
— поперечная сила в наклонном сечении;
![]() —
коэффициент, для тяжелого бетона
= 1,5; с
—
длина проекции
наклонного сечения; при расчете задаются
рядом значений
—
коэффициент, для тяжелого бетона
= 1,5; с
—
длина проекции
наклонного сечения; при расчете задаются
рядом значений
![]() с
целью определения наиневыгоднейшего.
с
целью определения наиневыгоднейшего.
