§ 4.3. Расчет прочности по наклонным сечениям

При поперечном изгибе балки вследствие совместного действия поперечной силы и изгибающего момента возникают главные растягивающие и главные сжимающие напряжения.

Разрушение может произойти вследствие достижения главными растягивающими напряжениями значения или главными сжимающими напряжениями . Проч­ность такого элемента при действии главных сжимающих и главных растягивающих напряжений будет обеспечена при

. (4.31)

Эти условия используются в качестве основы для по­лучения зависимостей, оценивающих максимальную и ми­нимальную несущую способность железобетонных эле­ментов по наклонным сечениям.

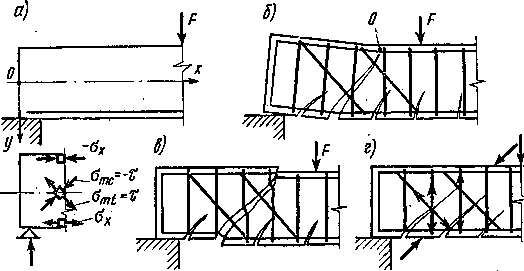
Рис. 4.6. Схемы действия главных напряжений (а) и разруше­ния изгибаемого элемента по наклонному сечению (б...г)

Для обеспечения прочности наклонных сечений изгибаемых элементов расчет должен производиться: а) на сжатие в полосе бетона стенки балки между наклонными трещинами (рис. 4.6, г);

б) по наклонной трещине на действие поперечной силы;

в) по наклонной трещине на действие изгибающего момента;

г) для элементов без поперечной арматуры — из условия, ограничивающего раз­витие наклонных трещин.

■ Расчет на сжатие в полосе бетона стенки балки между наклонными трещинами. При образовании на­клонных трещин бетон между ними испытывает действие главных сжимающих напряжений и одновременно растягивающих усилий от поперечной арматуры (см. рис. 4.6, г), т. е. находится в условиях двухосного напряжен­ного состояния (сжатие — растяжение). Прочность бето­на в этом случае будет ниже, чем при одноосном напряженном состоянии. Вследствие этого, а также других факторов для обеспечения прочности бетона на сжатие в полосе между наклонными трещинами (в элементе с по­перечной арматурой) должно соблюдаться условие (4.32), полученное с учетом формулы (4.31) и экспери­ментальных данных:

, (4.32)

где — коэффициент, учитывающий влияние попереч­ной арматуры, при хомутах, нормальных к оси элемента ; ; ; — площадь сечения одного хомута; n — число хомутов в сечении элемента; s — расстояние между хомутами; — для тяжелого бетона.

Если условие (4.32) не выполняется, необходимо уве­личить размеры сечения или повысить класс бетона.

■ Расчет элементов прямоугольного сечения по на­клонной трещине на действие поперечной силы. На­клонная трещина в элементе не образуется (см. форму­лу (4.31), если . Для железобетонных конструк­ций этому условию соответствует приближенная опытная зависимость

(4.33)

где — коэффициент, для тяжелого бетона . Таким образом, при соблюдении условия (4.33) рас­чет наклонных сечений по поперечной силе не требуется, и арматура может быть назначена по конструктивным соображениям. Если , то прочность сечения нужно обеспечить постановкой поперечной, а иногда и наклонной арматуры в соответствии с расчетом.

Р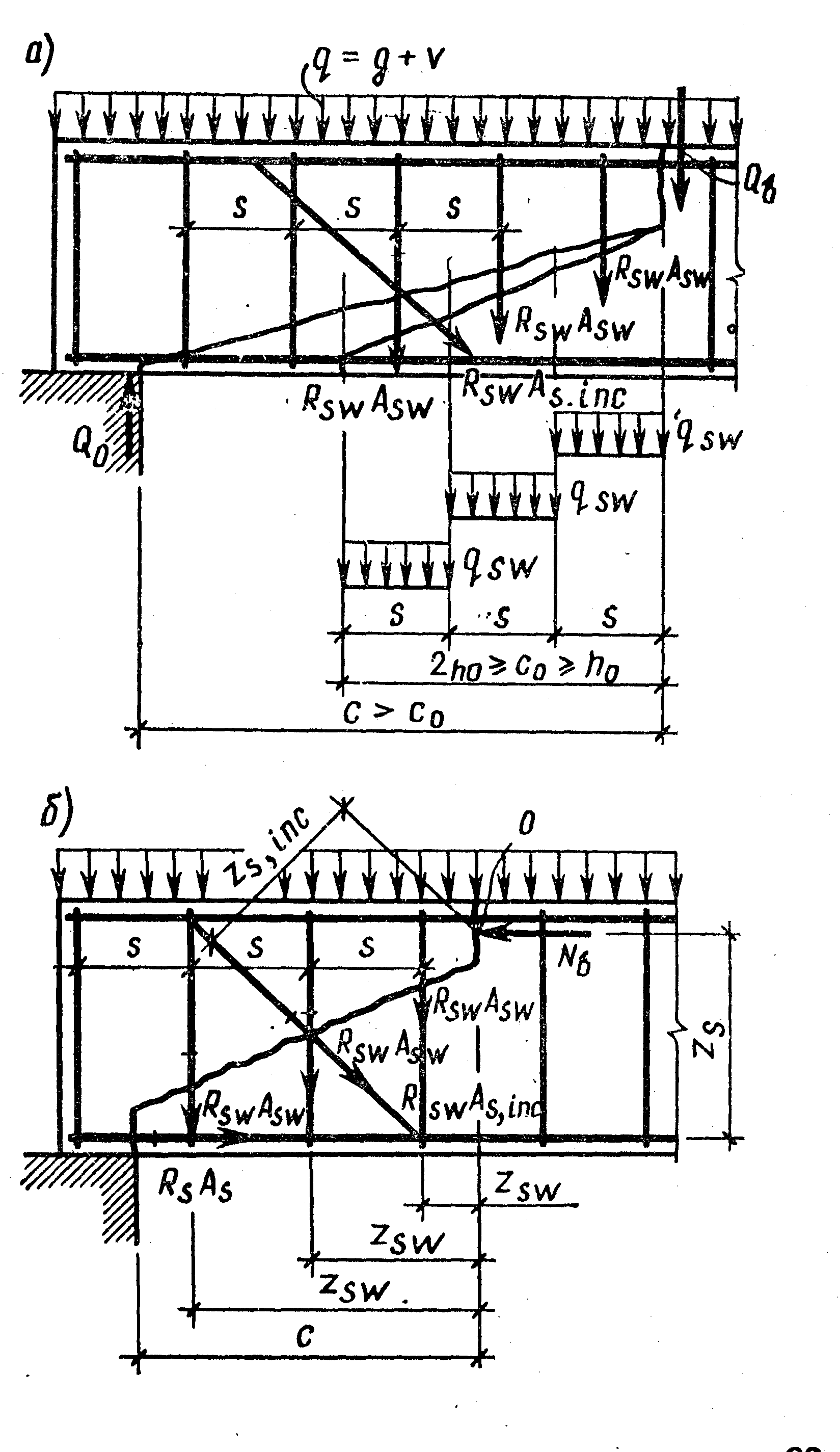 ис. 4.7. Схема расчетных усилий в наклонном се­чении:

а — при расчете на действие поперечной силы; б — на действие изгибающего момента.

Расчет хомутов. В практике проектирования наиболее распространено поперечное армирование только хомутами (без отгибов). В этом случае выражение (4.34) примет вид

, (4.35)

Поперечная сила, воспринимаемая бетоном над наклонной трещиной, определяется по эмпирической формуле

, (4.36)

но принимается не менее , где с — длина проекции наклонного сечения, представляющая собой расстояние от вершины наклонной трещины до опоры; и — коэффициенты, для тяжелого бетона , ; — коэффициент, учитывающий влияние про­дольных сил от внешних нагрузок и предварительного обжатия; для изгибаемых элементов без предваритель­ного напряжения .

Усилия, воспринимаемые хомутами, заменяются равномерно распределенными усилиями (рис. 4.7): , (4.37)

тогда , (4.38)

где — длина проекции наклонного сечения, на которой учитывается работа хомутов. Величина принимается не более .

Опыты показывают, что величина одновременно с ростом возрастает, но до определенного предела, от­вечающего минимуму . При этом значение оп­ределяют по формуле

(4.39)

и принимают в пределах .

При определении расчетной поперечной силы (см. рис. 4.7) нагрузку уменьшающую внешнюю поперечную силу, нужно полностью учитывать, лишь когда она безусловно действует (давление воды, грунта и т. п.). При ее учете

. (4.40)

Подставляя (4.36), (4.38) и (4.40) в (4.35) получают

. (4.4 1)

При проверке условия (4.41) задаются рядом наклонных сечений при различных значениях , не превышаю­щих расстояния от опоры до сечения с максимальным изгибающим моментом, и учитывают наиболее неблагоприятный результат.

Для исключения возможности образования трещин между двумя соседними хомутами необходимо, чтобы поперечная сила воспринималась только бетоном, в этом случае условие (4.36) примет вид . Тогда, приняв и вводя коэффициент 0,75, учитывающий неточности при установке хомутов, получим

. (4.42)

В соответствии с нормами [1] расстояние между поперечными стержнями в элементах, не имеющих отогнутой арматуры, в случаях, когда они ставятся по расчету или по конструктивным соображениям, принимают: а) на приопорных участках (равных при равномерной нагрузке пролета) для балок 450 мм — не более и не бо­лее 150 мм, а для балок мм — не более и не более 500 мм; б) на остальной части пролета при мм — не более и не более 500мм.