II. Решение типичных задач

Пример 0*. Найдите модуль и аргумент комплексного числа и запишите z в тригонометрической форме.

Решение. Модуль комплексного числа определяется по формуле . Значит, .

Так как , то точка лежит во II квадранте. Поэтому главное значение аргумента дается формулой [4, с.14] . Следовательно,

Все значения аргумента находятся по формуле

Тригонометрическая форма комплексного числа z имеет вид , где , argz. Значит,

Пример 1*. Вычислите все значения степенной функции в точке .

Решение. Степенная функция определяется соотношением [2, с.182] . Все значения логарифмической функции даются формулой [2, с.178] В нашем случае Так как точка лежит в третьем квадранте, то Значит,

Теперь получаем

Пример 2*. Найдите аналитическую функцию f(z) по заданной действительной части

Решение. Заданная функция u(x,y) является гармонической во всей плоскости, т.к.

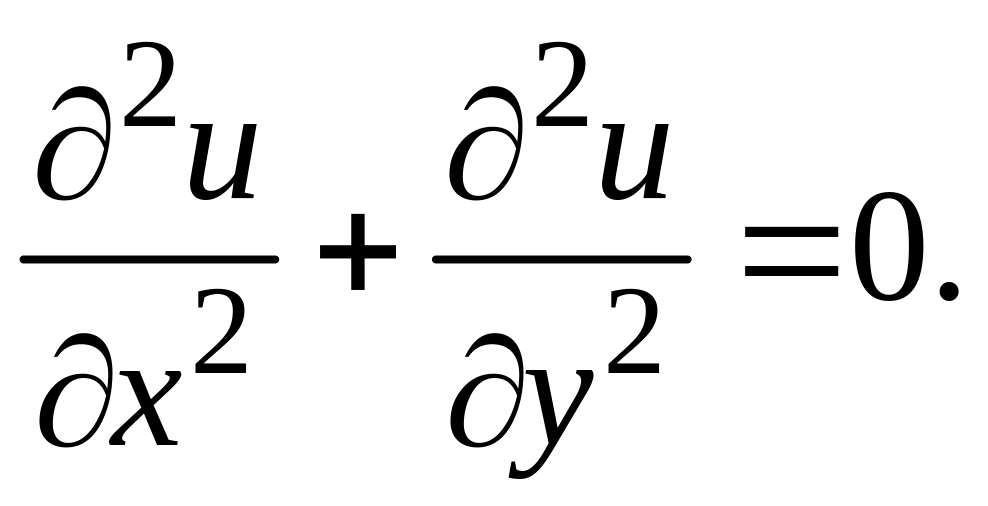
Для того, чтобы найти аналитическую функцию f(z), необходимо определить гармоническую функцию v(x,y)=Imf(z), сопряженную с заданной функцией u(x,y). Функции u(x,y) и v(x,y) связаны между собой условиями Коши-Римана (5). T.к. 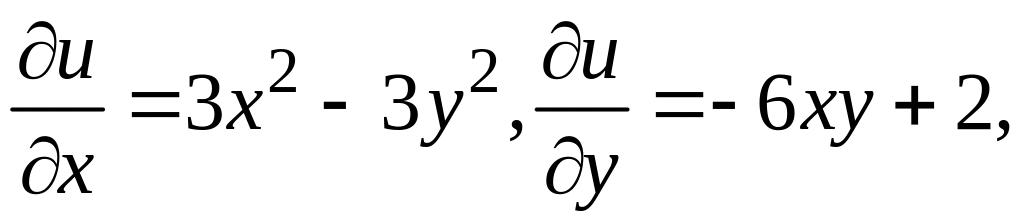то искомая функция v(x,y) является решением системы дифференциальных уравнений

Из первого уравнения находим

где c(x) – некоторая функция переменной x. Подставляя значение v(x,y) во второе уравнение системы, получим соотношение для определения c(x): Значит, и

Подставляя в это равенство значения и , где - число, комплексно сопряженное числу , окончательно найдем

Пример 3*. Найдите образ области при отображении функцией .

Решение. Заданная область E есть круг радиуса 2 с центром в начале координат. Его границей является окружность . Так как дробно-линейная функция конформно отображает расширенную комплексную плоскость на , то по принципу соответствия границ [2, с.128] граница области E отображается в границу * образа с сохранением ориентации.

Найдем образ окружности при отображении . Так как окружность не проходит через точку , то ее образом будет окружность. Поскольку , то окружность * проходит через точки и 2. Коэффициенты заданной дробно-линейной функции действительные числа, поэтому при отображении действительная ось переходит в действительную ось. Окружность ортогональна действительной оси на плоскости z. Следовательно, в силу конформности дробно-линейных отображений окружность * также будет ортогональна действительной оси на плоскости w. Значит отрезок будет диаметром окружности *, т.е. *= . Так как точка z=0, принадлежащая E, переходит в точку w(0)=0, лежащую внутри окружности *, то образом E при отображении будет круг .

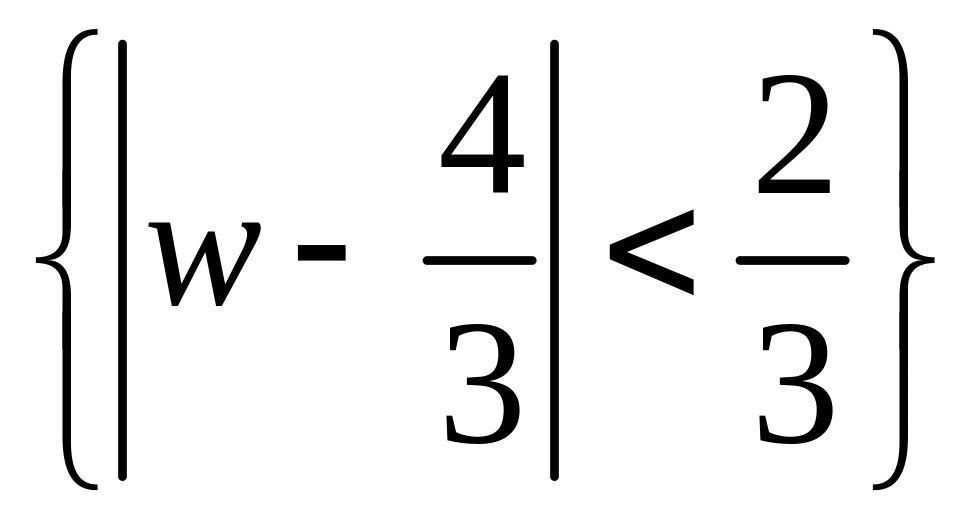Пример 4*. Найти дробно-линейное отображение, переводящее точки соответственно в точки

Решение. Используем общий вид дробно-линейного преобразования, переводящего три заданные точки в три другие заданные точки [2, с.53]:

Подставляя в эту формулу заданные значения и заменяя множители, содержащие , единицами, получим

Выражая w через z, имеем

Непосредственной проверкой легко убедиться в том, что эта функция удовлетворяет заданным условиям.

Пример 5*. Отобразить круг на верхнюю полуплоскость так, чтобы центр круга перешел в точку и

Решение. Для решения удобно воспользоваться общим видом отображения, переводящего верхнюю полуплоскость на круг . Так как искомое отображение является дробно-линейным, то точки, симметричные относительно действительной оси, должны перейти в точки, симметричные относительно окружности . Таким образом, должны выполняться условия Общий вид такого отображения дает формула

из которой имеем

Выражая w через z, получим

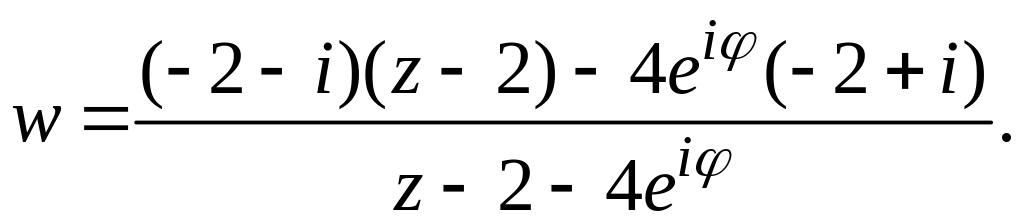
Вычислим значение Так как

то

По условию , следовательно, или Таким образом, искомое отображение имеет вид

Пример 6*. Отобразить круг на круг так, чтобы и w(-2)=0.

Решение. Так как искомое отображение дробно-линейное, то точка , симметричная точке относительно окружности , должна перейти в точку , симметричную точке относительно окружности . Поскольку точка , симметричная точке относительно окружности дается формулой [2, с.51]:

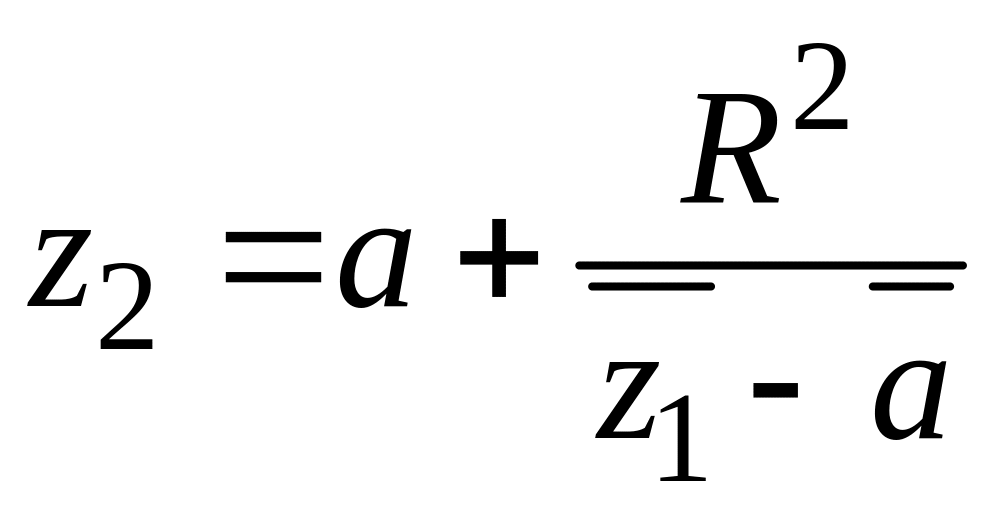, то

Строя по заданным точкам дробно-линейное отображение, получаем

Выражая w через z, находим искомое отображение

Непосредственной проверкой легко убедиться в том, что оно удовлетворяет заданным условиям.

Пример 7*. Отобразить внутренность круга с разрезом по отрезку на верхнюю полуплоскость.

Решение. Решим задачу поэтапно. Вначале повернем круг на угол : Отрезок перейдет в отрезок . К полученной области применим функцию Жуковского:

Единичная окружность перейдет в разрез по отрезку [-1,1], разрез по отрезку - в разрез по отрезку . Таким образом, круг с разрезом по отрезку отобразится на плоскость с разрезом по отрезку .

На следующем этапе дробно-линейной функцией отобразим полученную область на плоскость с разрезом по положительной полуоси. Это отображение построим по трем парам точек, переводя в в в

Отсюда Остается применить отображение , переводящее плоскость с разрезом по положительной полуоси на верхнюю полуплоскость.

Выражая последовательно все отображения через z, получим

.

Таким образом, искомое отображение определяется формулой

Пример 8*. Отобразить внешность касающихся кругов и на верхнюю полуплоскость.

Решение. Решим задачу поэтапно. Заметим, что точка z=0 одновременно принадлежит окружностям и действительной оси. Поэтому, если построить дробно-линейное отображение, переводящее z=0 в , то в силу кругового свойства образами указанных окружностей и действительной оси будут прямые (как обобщенные окружности, проходящие через точку ). Это отображение конформно, поэтому образы касающихся окружностей – параллельные прямые, а образ действительной оси – прямая, им перпендикулярная. При этом рассматриваемая область отобразится на полосу.

Зададим соответствие точек и построим по этим точкам дробно-линейную функцию

Выражая w через z, получим Так как по этой формуле действительным значениям z соответствуют чисто мнимые значения , то эта функция переводит действительную ось в мнимую ось. Тогда окружность переходит в прямую , а окружность - в прямую , которые перпендикулярны мнимой оси. При этом внешность окружности отобразится на полосу шириной , заключенную между указанными прямыми. Остается применить функцию переводящую данную горизонтальную полосу на верхнюю полуплоскость. Выражая последовательно все примененные функции через z, получим искомое отображение в виде

Пример 9*. Вычислить интеграл если , а L - парабола , соединяющая точки a=0, b=1+i.

Решение. Так как , то по формуле (8) получаем

.

Вычисляя криволинейные интегралы второго рода, получим

Пример 10*. Найти радиус сходимости степенного ряда

Решение. Чтобы воспользоваться формулой Коши-Адамара вычислим предел

.

Значит

Пример 11*. Разложить в ряд Тейлора в окрестности точки z=0 функцию

Решение. Понижая степень, преобразуем заданную функцию к виду

= .

Отсюда, используя ряд Тейлора функции , имеем

.

Пример 12*. Разложить в ряд Лорана функцию

в областях а)

Решение. Представим функцию f(z) в виде суммы простых дробей

(16)

что можно сделать, пользуясь методом неопределенных коэффициентов.

Если , то, используя формулу суммы геометрической прогрессии, получим

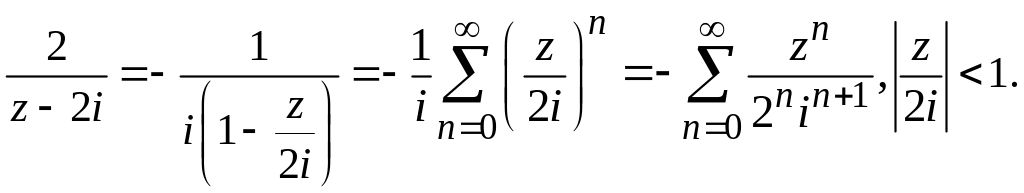(17)

Если , то, преобразуя исходное выражение к виду, где можно применить формулу суммы геометрической прогрессии, имеем

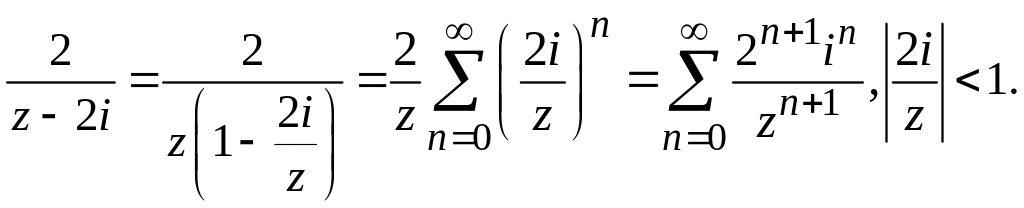(18)

Аналогично при имеем разложение

(19)

а если , то

(20)

а) В области в силу формул (16), (17), (19) функция f(z) разлагается в ряд Лорана

Этот ряд есть ряд Тейлора.

b) В области разложение функции f(z) в ряд Лорана в силу формул (16), (18), (19) имеет вид

Этот ряд содержит как положительные, так и отрицательные степени z.

c) В области в силу формул (16), (18), (20) функция f(z) представляется рядом Лорана, содержащим только отрицательные степени z.

Пример 13*. Найдите изолированные особые точки функции выясните их характер и исследуйте поведение функции на бесконечности.

Решение. Для функции точки являются нулями соответственно первого, второго и третьего порядков. Следовательно, для функции f(z) точки являются полюсами соответственно первого, второго и третьего порядков.

Точка является существенно особой для функции так как главная часть ряда Лорана этой функции в окрестности точки содержит бесконечное число членов: 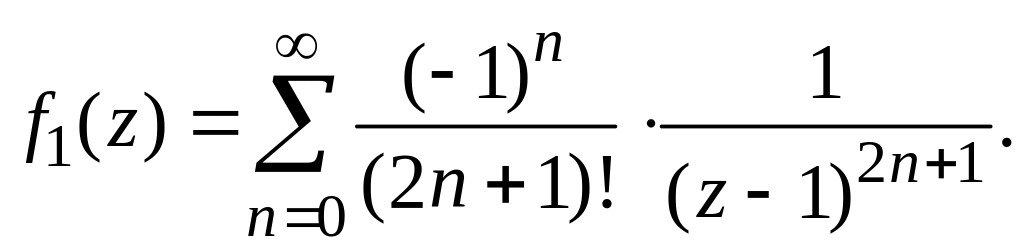Отсюда вытекает, что является существенно особой точкой и для функции f(z). Действительно, предполагаем противное: - устранимая особая точка или полюс. Тогда существует предел где если устранимая особая точка, и если - полюс. Отсюда следует, что

т.е. является устранимой особой точкой или полюсом для функции что приводит к противоречию. Поэтому - существенно особая точка для функции f(z).

При имеем

Поэтому получаем Следовательно, - полюс третьего порядка для функции f(z).

Пример 14*. Вычислить вычеты функции во всех изолированных особых точках.

Решение. Приравнивая нулю знаменатель, находим особые точки заданной функции

При этом - полюс второго порядка, а - полюсы первого порядка. Поэтому [2, с.226,227]

Пример 15*. Вычислить интеграл где C – положительно ориентированная окружность .

Решение. Способ I. Функция имеет в круге две особые точки: являющиеся полюсами второго порядка. Следовательно, по основной теореме о вычетах [2, с.145]

Вычисляя вычеты f(z) в указанных точках по формуле [2,с.147], имеем

Следовательно,

Способ II. Так как [2, с.148]

то

Поскольку при то точка является нулем первого порядка функции f(z) и

Следовательно,

Пример 16*. Вычислить интеграл от рациональной функции.

Решение. Функция имеет в верхней полуплоскости два полюса первого порядка в точках и Так как при то применяя формулу [3, с. 274] имеем

Поскольку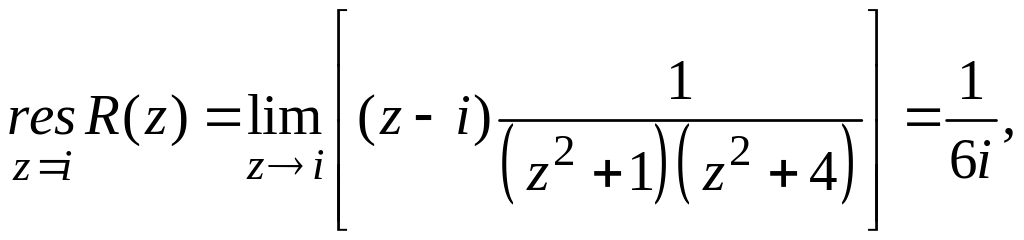 то

Пример 17*. Используя лемму Жордана вычислить интеграл

Решение. Так как при , то функция F(z) удовлетворяет условиям леммы Жордана. Поэтому [1,с.241]