Белорусский государственный университет Механико-математический факультет Кафедра теории функций

Теория функций комплексной переменной

Методическое пособие для студентов заочного отделения

механико-математического факультета

Минск, 2005

Предисловие

Теория функций комплексной переменной (ТФКП) называется также теорией аналитических функций или комплексным анализом. В учебной литературе, рекомендованной для изучения ТФКП, имеется много содержательных учебников [2-5, 7, 8]. Однако, они недостаточно приспособлены как по объему, так и по выбору материала к учебной программе по ТФКП для математических факультетов университетов Беларуси, в особенности для студентов заочных отделений.

Для комплексного анализа характерна относительная простота теоретических построений, однако овладение его конкретными методами вызывает обычно значительные трудности. Поэтому во время самостоятельного изучения комплексного анализа студентам рекомендуется большое внимание уделять решению задач. Указанные обстоятельства приняты во внимание авторами при написании данного пособия.

Пособие состоит из трех частей. В первой части приведена программа дисциплины «Теория функций комплексной переменной» и даны краткие теоретические сведения по всем ее разделам. Во второй части даны решения основных типичных задач указанного курса. В третьей части содержатся условия 10 вариантов контрольных работ №1, №2 по ТФКП для студентов-заочников.

Пособие предназначено для студентов заочного отделения механико-математического факультета Белорусского госуниверситета. Оно может быть использовано при проведении лабораторных и контрольных работ для студентов очной формы обучения отделений «математическая электроника», «компьютерная математика», «математическая экономика», «механика», а так же для студентов других факультетов.

I.Методические указания

Теория функций комплексной переменной (ТФКП) называется также теорией аналитических функций или комплексным анализом. Программа этого курса приводится в настоящем пособии. Объем теоретического материала, охватываемый этой программой, примерно соответствует содержанию учебников [1]-[4].

Для комплексного анализа характерна относительная простота теоретических построений, однако, овладение конкретными методами комплексного анализа вызывает обычно значительные трудности. В связи с этим во время самостоятельного изучения комплексного анализа студентам рекомендуется больше внимания уделять решению задач.

Программа дисциплины «Теория функций комплексной переменной»

1.Введение. Предмет ТФКП. Краткий обзор развития ТФКП и ее роль в математике и приложениях.

2.Комплексные числа. Комплексное число, его изображение на плоскости, модуль и аргумент комплексного числа. Последовательности и пределы, ряды. Расширенная комплексная плоскость, сфера Римана.

3.Функции комплексной переменной. Функция, ее действительная и мнимая части. Предел функции, непрерывность.

4.Дифференцируемые функции. Производная. Дифференцируемость по комплексной переменной; условия Коши-Римана. Аналитические (голоморфные) функции. Геометрический смысл аргумента и модуля производной. Понятие о конформных отображениях.

5.Элементарные функции и конформные отображения. Линейная и дробно-линейная функции, показательная функция и логарифм, степень с произвольным показателем, функция Жуковского. Понятие об однолистности, о многозначных аналитических функциях и римановых поверхностях. Применение элементарных функций к конформным отображениям.

6.Интеграл. Интеграл по комплексной переменной. Первообразная, формула Ньютона-Лейбница. Интегральная теорема Коши для простого и составного контуров.

7.Интегральная формула Коши. Интегральная формула Коши. Интеграл типа Коши. Бесконечная дифференцируемость аналитических функций, формулы Коши для производных аналитических функций. Теорема Морера.

8.Последовательности и ряды аналитических функций. Функциональные последовательности и ряды. Теорема Вейерштрасса о последовательностях и рядах аналитических функций.

9.Степенной ряд. Степенной ряд. Радиус сходимости. Формула Коши-Адамара. Аналитичность суммы степенного ряда. Разложение аналитической функции в степенной ряд, единственность разложения, ряд Тейлора. Действия над степенными рядами.

10.Ряд Лорана. Ряд Лорана, область его сходимости. Разложение аналитической функции в ряд Лорана, единственность разложения. Формулы для коэффициентов разложения, неравенства Коши. Теорема об устранимой особой точке и теорема Лиувилля.

11.Теорема единственности и принцип максимума. Нули аналитических функций, порядок нуля. Теорема единственности для аналитических функций. Принцип максимума модуля. Лемма Шварца.

12.Изолированные особые точки однозначного характера. Классификация изолированных особых точек однозначного характера. Полюс и существенно особая точка, различные их определения. Случай бесконечно удаленной точки. Теорема Сохоцкого. Понятие о теореме Пикара.

13.Вычеты. Принцип аргумента. Определение вычета. Теорема о вычетах. Формулы для вычисления вычетов. Применение к вычислению интегралов. Логарифмический вычет; принцип аргумента. Теорема Руше.

14.Аналитическое продолжение. Аналитический элемент и его продолжение. Аналитическое продолжение через границу области. Принцип симметрии.

15.Отображения посредством аналитических функций. Принцип сохранения области. Достаточное условие однолистности. Конформные отображения. Понятие о теореме Римана и о соответствии границ при конформном отображении.

16.Целые и мероморфные функции. Порядок и тип целой функции. Понятие о теореме Вейерштрасса. Мероморфные функции.

17.Гармонические функции. Гармонические функции, их связь с аналитическими. Принцип максимума, теорема единственности. Теорема о среднем. Интегралы Пуассона и Шварца.

18.Гидромеханическое истолкование аналитических функций. Плоскопараллельный поток идеальной несжимаемой жидкости без источников, стоков и вихрей. Потенциал скоростей, функция тока, характеристическая функция потока.

Дадим методические указания по изучению основных вопросов программы ТФКП.

1.Введение. Этот материал приведен в предисловии к учебнику [2] и во введении к [3].

2.Комплексные числа. Этот материал имеется во всех учебниках. Комплексные числа можно определить, например, как числа вида , где , . Множество всех комплексных чисел является полем, содержащим множество всех вещественных чисел в качестве подполя.

Каждое комплексное число изображается точкой (x,y) плоскости или радиус-вектором этой точки. Длина радиус-вектора точки z называется модулем, а угол его наклона к оси Ox – аргументом комплексного числа z. Обозначения: и Arg z соответственно.

Рис.1

Из рис.1видно, что , а Arg z удовлетворяет системе уравнений

(1)

В связи с этим комплексное число представляется в различных формах: алгебраической и тригонометрической , каждая из которых обладает своими преимуществами.

Понятие последовательности комплексных чисел, ее предела, ряда с комплексными членами, его суммы в принципе не отличаются от соответствующих понятий в вещественном случае.

Добавляя к элемент (бесконечно удаленную точку), получим расширенную комплексную плоскость .

3.Функции комплексной переменной. Согласно [1,§4] - это отображения вида , где A- некоторое подмножество . Обычно в качестве A берется область, т.е. открытое и связное подмножество .

Для наглядного изображения функции комплексной переменной берутся две комплексные плоскости. На плоскости переменной z рисуют некоторые геометрические объекты (например, сетки координатных линий), а на плоскости w – образы этих геометрических объектов. Понятия предела и непрерывности функций комплексной переменной определяются так же, как и для функций вещественной переменной. Остаются справедливыми и основные факты теории пределов и непрерывности, кроме тех, которые связывают эти понятия с отношением >.

Полагая , где перепишем уравнение в виде равносильной системы

(2)

Таким образом, функцию комплексной переменной можно задать в равносильном виде (2), т.е. как отображение из в . Понятия предела и непрерывности отображения (2) равносильны соответствующим понятиям для функции .

4.Дифференцируемые функции. Производная.[1,§7]. Для целей дифференциального исчисления удобно предполагать, что рассматриваемая функция определена в области.

Функция называется -дифференцируемой в точке z, если существует такая постоянная , что

, . (3)

Производная в точке z от функции определяется тем же соотношением, что и для функции вещественной переменной:

. (4)

Отсюда и из того, что операции над комплексными числами подчиняются тем же законам, что и операции над вещественными числами, следует, что вся техника вычисления производных от функций комплексной переменной такая же, как и для функций вещественной переменной.

Различие между понятиями производной для функций вещественной и комплексной переменной заключается в том, что стремление к нулю приращения h происходит по-разному. В вещественном случае по одномерному множеству, а в комплексном – по двумерному. Это различие ведет к следующему факту.

Существование конечной производной (4) в точке z равносильно -дифференцируемости функции f в этой точке. Полагая f=u+iv, запишем условия -дифференцируемости функции f в виде

, (5)

где дифференцируемы как функции двух действительных переменных. Напомним, что для дифференцируемости достаточно существования и непрерывности частных производных первого порядка этих функций.

Соотношения (5) называются условиями Коши-Римана. С понятием -дифференцируемости связано важнейшее в ТФКП понятие аналитической функции. Функция называется аналитической в точке z, если она -дифференцируема в некоторой окрестности точки z. Если функция - аналитическая в точке , то в окрестности точки имеет место приближенное равенство

, (6)

которое тем точнее, чем меньше .

Рассматривая функцию как преобразование (отображение в себя) плоскости z, из (6) при заключаем, что в малой окрестности точки отображение f ведет себя как преобразование подобия. Вытекающие из (6) равенства

,

выражают геометрический смысл модуля и аргумента производной (модуль производной – коэффициент растяжения, аргумент производной – угол поворота окрестности точки ).

Отображение называется конформным в точке , если его дифференциал как функция от h отличен от тождественного нуля и сводится к композиции растяжения и поворота. Устанавливается, что конформность отображения в точке равносильна условию . Конформные отображения в области определяются как конформные в каждой точке области. Тем самым устанавливается, что конформные в области отображения могут реализоваться только аналитическими функциями.

5.Элементарные функции и конформные отображения. [2,§3,4]. Аналитические функции и , где называются соответственно линейной и дробно-линейной. Линейная функция, очевидно, является частным случаем дробно-линейной при .

Отметим важнейшие свойства дробно-линейных функций.

1.Любая дробно-линейная функция реализует конформный гомеоморфизм на .

2.Дробно-линейная функция отображает любую -окружность на некоторую -окружность. (Под -окружностью понимается либо обычная окружность, либо прямая линия, к которой присоединена точка .)

3.Дробно-линейная функция любую пару точек, симметричных относительно -окружности отображает на пару точек, симметричных относительно образа этой -окружности.

Экспонента комплексной переменной определяется равенством

. (7)

Эта функция аналитична на , что устанавливается непосредственно проверкой условий Коши-Римана (5).

Кроме очевидных свойств и экспонента обладает свойством периодичности с чисто мнимым периодом, целократным числу .

Областью однолистности экспоненты является горизонтальная полоса шириной не большей . Образом полосы при отображении (7) будет угол .

В частности, образом полосы является плоскость с разрезом по положительному лучу действительной оси.

Логарифмическая функция комплексной переменной определяется как функция, обратная к экспоненте (7), откуда вытекает ее аналитичность. Полагая , где , имеем:

,

т.е. функция Lnz бесконечнозначная. При она реализует конформное отображение угла на полосу .

Функцией Жуковского называется рациональная функция . Она аналитична всюду на , кроме точки z=0, реализует конформное отображение круга и его внешности на плоскость с разрезом по прямолинейному отрезку [-1,1].

Тригонометрические и гиперболические функции определяются соотношениями:

, , , .

Эти функции представимы в виде композиций уже известных функций (линейной, экспоненты, функции Жуковского). Отсюда следует их аналитичность, а также характер реализуемых ими конформных отображений.

Общая степенная функция вводится соотношением и является бесконечнозначной функцией при .

6.Интеграл. [1, §9]. Криволинейный интеграл по комплексной переменной – это по существу хорошо известный из вещественного анализа криволинейный интеграл второго рода.

Полагая , определяем:

. (8)

При дополнительном предположении непрерывности частных производных условия Коши-Римана (5) выражают известные из анализа условия независимости интеграла (8) от пути. Это и есть одна из форм центральной теоремы курса – интегральной теоремы Коши.

Если контур интегрирования замкнут и лежит в односвязной области D, где функция f аналитична, то

.

7.Интегральная формула Коши. [1, §10]. Пусть D - область с кусочно-гладким краем . Стандартная ориентация края выбирается так, что при движении точки вдоль края в положительном направлении область D остается слева. Если , функция f аналитична в D и непрерывна на , то

(9)

Это и есть интегральная формула Коши или интеграл Коши. Если - произвольная непрерывная функция, то функция

называется интегралом типа Коши. При интеграл типа Коши является аналитической функцией переменной z. Формулы для производных от аналитической функции f(z) получаются путем дифференцирования под знаком интеграла Коши (9). Теорему Мореры можно рассматривать как теорему, обратную к интегральной теореме Коши.

8.Последовательности и ряды аналитических функций. Виды сходимости функциональных последовательностей и рядов (поточечная, равномерная, в среднем) изучаются в курсе вещественного анализа. Характерной для комплексного анализа является сходимость равномерная внутри области D, т.е. сходимость равномерная на любом компакте K, содержащемся в области D. Теорема Вейерштрасса об аналитичности суммы равномерно сходящегося на компакте K ряда аналитических функций, изложены в [1, п.2,3].

9.Степенной ряд. [1, §11]. Степенным рядом называется функциональный ряд вида

(10)

где - числовая последовательность. Для любого степенного ряда существует радиус сходимости , вычисляемый по формуле Коши- Адамара

Открытый круг называется кругом сходимости степенного ряда (10). Степенной ряд сходится абсолютно в круге сходимости, сходится равномерно на любом компакте, лежащем в круге сходимости, расходится во всех точках, внешних по отношению к кругу сходимости. Для ответа на вопрос о сходимости ряда (10) на окружности требуются дополнительные исследования.

10.Ряд Лорана. [1, §17]. Если функция f(z) аналитична в кольцевой области , то она представима в ней в виде суммы ряда

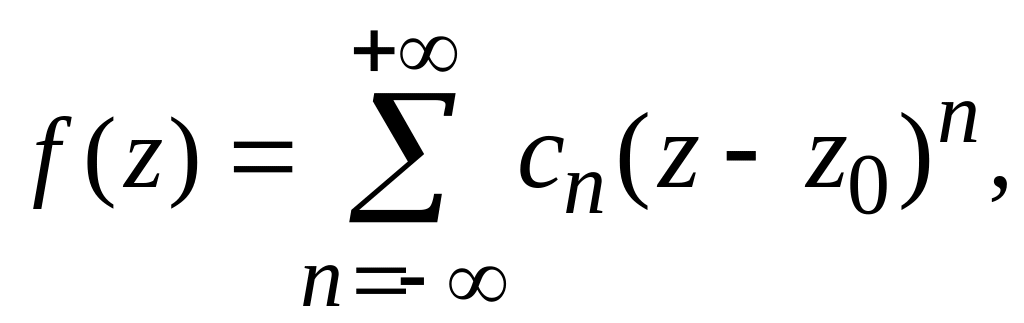(11)

где

(12)

Ряд (11) называется рядом Лорана с центром функции f(z). Если , то ряд Лорана переходит в ряд Тейлора.

11.Теорема единственности и принцип максимума. [1, §14]. Нулем аналитической функции f(z) называется любая точка , в которой . В окрестности точки функция f представима в виде , где , . Число n называется порядком нуля . Теорема единственности утверждает, что если множество нулей функции f имеет предельную точку, лежащую внутри области аналитичности, то . Из теоремы единственности вытекает свойство изолированности нулей аналитической функции, состоящее в том, что в некоторой окрестности нуля аналитической функции нет других нулей.

Принцип максимума заключается в том, что модуль функции , отличный от тождественной постоянной, не может иметь точек максимума внутри области аналитичности .

12.Изолированные особые точки однозначного характера. [1, §18]. Точка называется особой для аналитической функции f, если в точке функция f не является аналитической. Особая точка называется изолированной, если существует окрестность точки такая, что f аналитична всюду в . Изолированные особые точки могут быть классифицированы в зависимости от поведения функции f при .