44. Волновая функция, ее статистический смысл. Соотношение неопределенностей Гейзенберга

Следует говорить о волновой функции, которая описывает микросостояние системы, её волновые свойства.

Де Бройль связал со свободно движущейся частицей плоскую волну. Известно, что плоская волна, распространяющаяся в направлении оси х описывается уравнением

или в экспоненциальной форме

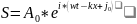
Заменив в соответствии и 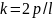через Е и p, уравнение волны де Бройля для свободной частицы пишут в виде

(в квантовой механике показатель экспоненты берут со знаком минус, но поскольку физический смысл имеет 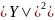, то это несущественно).

Функцию Y называют волновой функций или пси-функцией. Она, как правило, бывает комплексной.

Интепретацию волновой функции дал в 1926 г. Борн: квадрат модуля волновой функции определяет вероятность того , что частица будет обнаружена в пределах объема :

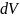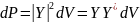
где 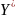- комплексно - сопряженная волновая функция.

Величина 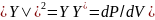- имеет смысл плотности вероятности.

Интеграл, взятый по всему пространству, должен равняться единице (вероятность достоверного события ). 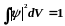(1)

Выражение (1) называют условием нормировки.

Отметим еще раз, что волновая функция описывает микросостояние частицы, ее волновые свойства и она позволяет ответить на все вопросы, которые имеет смысл с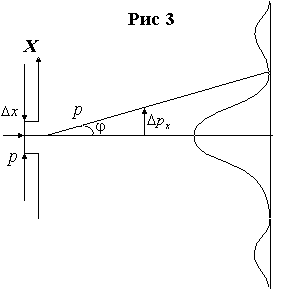 тавить.

Соотношение неопределённостей Гейзенберга.

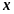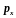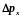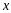Попытаемся определить значение координаты свободно летящей микрочастицы, поставив на ее пути щель шириной , расположенную перпендикулярно к направлению движения частицы. До прохождения частицы через щель имеет точное значение, равное 0, так что неопределенность импульса = 0, зато координата частицы является совершенно неопределенной. В момент прохождениячастицы через щель положение меняется. Вместо полной неопределенности координаты 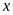появляется неопределенность 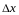, но это достигается ценой утраты определенности значения 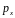. Действительно, в следствии дифракции имеется некоторая вероятность того, что частица будет двигаться в пределах некоторого угла 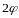, где 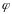- угол, соответствующий первому дифракционному минимуму. Таким образом, появляется неопределенность импульса 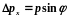. Краю центрального дифракционного максимума (первому минимуму), получающемуся от щели шириной соответствует угол 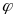, для которого 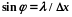.Следовательно 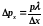.Получаем соотношение : .

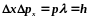В общем случае соотношение называют соотношением неопределенностей Гейзенберга. Из него следует, что чем точнее определена координата (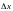 мало, т.е. узкая щель), тем больше неопределенность в импульсе частицы 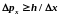. Точность определения импульса будет возрастать с увеличением ширины щел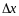и и при 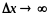не будет наблюдаться дифракционная картина, и поэтому неопределенность импульса 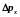будет такой же, как и до прохождения частицы через щель, т.е. 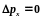. Но в этом случае не определена координата частицы, т.е. . Невозможность одновременно точно определить координату и импульс (скорость) не связана с несовершенством методов измерения или измерительных приборов. Соотношение неопределенности является квантовым ограничением применимости классической механики к микрообъектам.

Выразим в виде 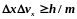. В квантовой механике рассматривается также соотношение неопределенностей между энергией частицы 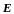и временем 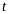нахождения частицы в данном энергетическом состоянии (или времени наблюдения за состоянием частицы). Оно аналогично и имеет вид .

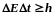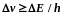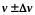Следует, что частота излучения фотона также должна иметь неопределённость , т.е. линии спектра должны характеризоваться частотой . Действительно, опыт показывает, что все спектральные линии размыты.