5. Момент силы, момент импульса материальной точки и системы материальных точек.

В физике момент силы можно понимать как «вращающая сила». В системе СИ единицами измерения для момента силы является ньютон-метр, Символ момента силы M . Момент силы иногда называют моментом пары сил. Вращающиеся аналоги силы, массы и ускорения есть момент силы, момент инерции и угловое ускорение соответственно. Сила, приложенная к рычагу, умноженная на расстояние до оси вращения рычага, есть момент силы. Более точно, момент силы частицы определяется как векторное произведени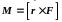е: , где  — сила, действующая на частицу, а  — радиус-вектор частицы.

Моментом силы F относительно некоторой точки О (расположенной на оси вращения) называют физическую векторную величину, численно равную произведению модуля этой силы и длины перпендикуляра (плеча), проведённого из данной точки на линию действия силы, т. е. M(F)=Fd.

Вектор момента силы направлен вдоль оси вращения. Его направление определяется по правилу буравчика, согласно которого, если ручка буравчика поворачивается в направлении вращения, то его остриё движется в направлении вектора момента силы.

Моме́нт и́мпульса характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение.

Момент импульса частицы относительно некоторого начала отсчёта определяется векторным произведением ее радиус-вектора и импульса:

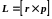
где  — радиус-вектор частицы относительно выбранного неподвижного в данной системе отсчёта начала отсчёта,  — импульс частицы.

В системе СИ момент импульса измеряется в единицах джоуль-секунда; Дж·с.

Из определения момента импульса следует его аддитивность. Так, для системы частиц выполняется выражение:

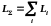
Таким образом, 2 закон Ньютона в случае вращательного движения можно сформулировать следующим образом:

В инерциальной системе отсчёта изменение момента импульса тела равно импульсу момента равнодействующей всех сил, действующих на это тело, относительно оси вращения.

6. Осевой момент инерции материальной точки и системы материальных точек. Теорема Штейнера

Момент инерции — скалярная физическая величина, мера инертности тела во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).Единица измерения СИ: кг·м².Обозначение: I или J.

Различают несколько моментов инерции — в зависимости от многообразия, от которого отсчитывается расстояние точек.

Осевой момент инерции. Осевые моменты инерции некоторых тел.

Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина Ja, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси: 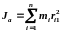, где: m_i — масса i-й точки, r_i — расстояние от i-й точки до оси.

Осевой момент инерции тела Ja является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности в поступательном движении.

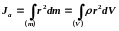где: dm = ρdV — масса малого элемента объёма тела dV, ρ — плотность, r — расстояние от элемента dV до оси a.

Если тело однородно, то есть его плотность всюду одинакова, то

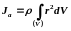
Теорема Гюйгенса-Штейнер

Момент инерции твёрдого тела относительно какой-либо оси зависит не только от массы, формы и размеров тела, но также от положения тела по отношению к этой оси. Согласно теореме Штейнера (теореме Гюйгенса-Штейнера), момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела Jc относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями: 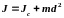. Если — момент инерции тела относительно оси, проходящей через центр масс тела, то момент инерции относительно параллельной оси, расположенной на расстоянии от неё, равен 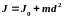,где 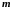— полная масса тела.

Например, момент инерции стержня относительно оси, проходящей через его конец, равен:

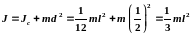
7. Основное уравнение динамики вращательного движения

Динамика вращательного движения материальной точки.

Основные параметры: момент силы, момент импульса, момент инерций. Основной закон динамики вращательного движения.

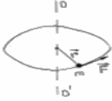
а) Пусть материальная точка массы m вращается относительно оси ОО΄. Обозначим r - радиус-вектор, проведенный от оси вращения до точки приложения силы F (Рисунок 10).Моментом силы F относительно оси вращения называется вектор M, равный векторному произведению радиус-вектора на вектор силы M = [r∙F] и направленный по оси вращения в сторону, определяемую по правилу правого буравчика. Модуль вектора момента силы равен M = F∙r∙sinα, где α - угол между векторами r и F.

Момент инерции.

При изучении вращения твердого тела пользуются понятием момента инерции. Моментом инерции системы (тела) относительно оси вращения называется физическая величина, равная сумме произведений масс n материальных точек системы на квадраты их расстояний до рассматриваемой оси: 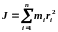. В случае непрерывного распределения масс эта сумма сводится к интегралу , где интегрирование производится по всему объему тела.

Величина r в этом случае есть функция положения точки с координатами x, y, z.

Для тела, которое вращается вокруг оси, 2 закон Ньютона формулируется следующим образом: В инерциальной системе отсчёта момент равнодействующей всех сил, приложенных к телу, относительно оси вращения равен произведению момента инерции этого тела и сообщаемого ему углового ускор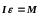ения: – это выражение называется основным уравнением динамики вращательного движения.