84.8 Где интегрирование можно производить вдоль любой линии, соединяющей начальную и конечную точки, так как работа сил электростатического поля не зависит от траек­тории перемещения.

Если перемещать заряд Q₀ из произвольной точки за пределы поля, т. е. в бесконеч­ность, где, по условию, потенциал равен нулю, то работа сил электростатического поля, согласно (84.6), A_=Q₀, откуда 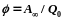84.9

Таким образом, потенциал — физическая величина, определяемая работой по переме­щению единичного положительного заряда при удалении его из данной точки поля в бесконечность. Эта работа численно равна работе, совершаемой внешними силами (против сил электростатического поля) по перемещению единичного положительного заряда из бесконечности в данную точку поля.

Из выражения (84.4) следует, что единица потенциала — вольт (В): 1 В есть потен­циал такой точки поля, в которой заряд в 1 Кл обладает потенциальной энергией 1 Дж (1 В = 1 Дж/Кл). Учитывая размерность вольта, можно показать, что введенная единица напряженности электростатического поля действительно равна 1 В/м: 1 Н/Кл=1 Нм/(Клм)=1 Дж/(Клм)=1 В/м.

Из формул (84.3) и (84.4) вытекает, что если поле создается несколькими зарядами, то потенциал поля системы зарядов равен алгебраической сумме потенциалов полей всех этих зарядов:

22. Электрический диполь. Потенциал и напряженность поля диполя

Принцип суперпозиции применим для расчета электростатического поля элект­рического диполя. Электрический диполь — система двух равных по модулю разноименных точечных зарядов (+Q,–Q), расстояние l между которыми значительно меньше расстояния до рассматриваемых точек поля. Вектор, направленный по оси диполя (прямой, проходящей через оба заряда) от отрицательного заряда к положи­тельному и равный расстоянию между ними, называется плечом диполя 1. Вектор 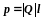(80.3) совпадающий по направлению с плечом диполя и равный произведению заряда |Q| на плечо l, называется электрическим моментом диполя или дипольным моментом.

Согласно принципу суперпозиции (80.2), напряженность Е поля диполя в произ­вольной точке 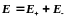_, где Е₊ и Е_– — напряженности полей, создаваемых соответственно положительным и отрицательным зарядами. Воспользовавшись этой формулой, рассчитаем напряжен­ность поля в произвольной точке на продолжении оси диполя и на перпендикуляре к середине его оси.

1. Напряженность поля на продолжении оси диполя в точке а. Как видно из рисунка, напряженность поля диполя в точке а направлена по оси диполя и по модулю равна

Обозначив расстояние от точки А до середины оси диполя через r, на основании формулы (79.2) для вакуума можно записать

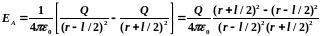
Согласно определению диполя, l/2<<r, поэтому

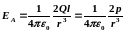
2. Напряженность поля на перпендикуляре, восставленном к оси из его середины, в точке в (рис. 123). Точка в равноудалена от зарядов, поэтому

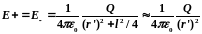(80.4)

где r' — расстояние от точки В до середины плеча диполя. Из подобия равнобедренных треугольников, опирающихся на плечо диполя и вектор Е_B, получим

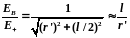
откуда 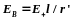(80.5)

Подставив в выражение (80.5) значение (80.4), получим

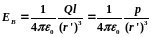
Вектор Е_B имеет направление, противоположное вектору электрического момента диполя (вектор р направлен от отрицательного заряда к положительному).