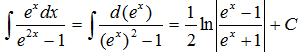29. Найти одз и точки разрыва функции.

• Найти точки пересечения графика функции с осями координат.

• Провести исследование функции с помощью первой производной, то есть найти точки экстремума функции и интервалы возрастания и убывания.

• Исследовать функцию с помощью производной второго порядка, то есть найти точки перегиба графика функции и интервалы его выпуклости и вогнутости.

• Найти асимптоты графика функции: а) вертикальные, b) наклонные.

• На основании проведенного исследования построить график функции.

Заметим, что перед построением графика полезно установить, не является ли данная функция четной или нечетной.

Вспомним, что функция называется четной, если при изменении знака аргумента значение функции не меняется: f(-x) = f(x) и функция называется нечетной, если f(-x) = -f(x).

В этом случае достаточно исследовать функцию и построить её график при положительных значениях аргумента, принадлежащих ОДЗ. При отрицательных значениях аргумента график достраивается на том основании, что для четной функции он симметричен относительно оси Oy, а для нечетной относительно начала координат.

Примеры. Исследовать функции и построить их графики.

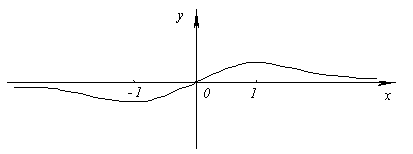
Область определения функции D(у)= (–∞; +∞). Точек разрыва нет.

Пересечение с осью Ox: x = 0,у=0.

Функция нечетная, следовательно, можно исследовать ее только на промежутке [0, +∞).

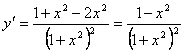
Критические точки: x1 = 1; x2= –1.

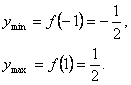
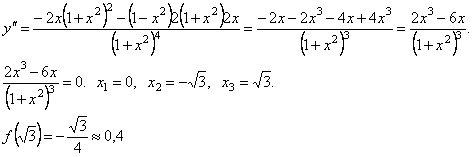
а) Вертикальных асимптот нет

б) . Асимптота – y = 0.

30 . Первообразная и неопределенный интеграл

Первообразной функцией для функции f(x) называется такая функция F(х), производная которой равна данной функции

F'(x) = f(x).

Обозначение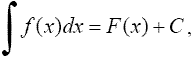

где F'(x) = f(x). Функция f(x) называется подынтегральной функцией, а выражение f(x)dx - подынтегральным выражением.

Свойства неопределенного интеграла

1°. Производная неопределенного интеграла равна подынтегральной функции; дифференциал от неопределенного интеграла равен подынтегральному выражению, т.е.

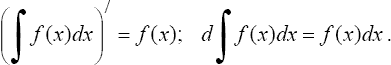
2°. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной, т.е.

3°. Постоянный множитель можно вынести из под знака интеграла, т.е. если k = const ≠ 0, то

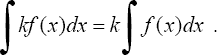
4° . Неопределенный интеграл от алгебраической суммы двух функций равен алгебраической сумме интегралов от этих функций в отдельности.

Свойство первообразной

• Первообразная суммы равна сумме первообразных

• Первообразная произведения константы и функции равна произведению константы и первообразной функции

• Достаточным условием существования первообразной у заданной на отрезке функции 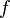является непрерывность на этом отрезке

• Необходимыми условиями существования являются принадлежность функции первому классу Бэра и выполнение для неё свойства Дарбу

• У заданной на отрезке функции любые две первообразные отличаются на постоянную.

31.

Свойства неопределенного интеграла

1°. Производная неопределенного интеграла равна подынтегральной функции; дифференциал от неопределенного интеграла равен подынтегральному выражению, т.е.

2°. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной, т.е.

3°. Постоянный множитель можно вынести из под знака интеграла, т.е. если k = const ≠ 0, то

4° . Неопределенный интеграл от алгебраической суммы двух функций равен алгебраической сумме интегралов от этих функций в отдельности.

32. Основные методы интегрирования

Для вычисления данного интеграла мы должны, если это возможно, пользуясь теми или другими способами, привести его к табличному интегралу и таким образом найти искомый результат. В нашем курсе мы рассмотрим лишь некоторые, наиболее часто встречающиеся приемы интегрирования и укажем их применение к простейшим примерам.

Наиболее важными методами интегрирования являются:

1) метод непосредственного интегрирования (метод разложения),

2) метод подстановки (метод введения новой переменной),

3) метод интегрирования по частям.

I. Метод непосредственного интегрирования

Задача нахождения неопределенных интегралов от многих функций решается методом сведения их к одному из табличных интегралов.

Пример 1.

∫(1-√x)2dx=∫(1-2√x+x)dx=∫dx-∫2√xdx+∫xdx=∫dx-2∫xdx+∫xdx=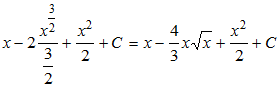

Пример 2.

Пример 3. ∫sin2xdx

Так как sin2x=(1-cos2x), то

∫sin2xdx=(1-cos2x)dx=∫dx-∫cos2xd(2x)=x-sin2x+C

Пример 4. ∫sinxcos3xdx

Так как sinxcos3x=(sin4x-sin2x), то имеем

∫sinxcos3xdx=∫(sin4x-sin2x)dx=∫sin4xd(4x)-∫sin2xd(2x)=-cos4x+cos2x+C

II. Метод подстановки (интегрирование заменой переменной)

Если функция x=φ(t) имеет непрерывную производную, то в данном неопределенном интеграле ∫f(x)dx всегда можно перейти к новой переменной t по формуле

∫f(x)dx=∫f(φ(t))φ'(t)dt

Затем найти интеграл из правой части и вернуться к исходной переменной. При этом, интеграл стоящий в правой части данного равенства может оказаться проще интеграла, стоящего в левой части этого равенства, или даже табличным. Такой способ нахождения интеграла называется методом замены переменной.

Пример 5. ∫x√x-5dx

Чтобы избавиться от корня, полагаем √x-5=t. Отсюда x=t2+5 и, следовательно, dx=2tdt. Производя подстановку, последовательно имеем:

∫x√x-5dx=∫(t2+5)•2tdt=∫(2t4+10t2)dt=2∫t4dt+10∫t2dt=

Пример 7.