17. Двухслойная" сложная функция записывается в виде

где u = g(x) - внутренняя функция, являющаяся, в свою очередь, аргументом для внешней функции f.

Если f и g - дифференцируемые функции, то сложная функция также дифференцируема по x и ее производная равна

Данная формула показывает, что производная сложной функции равна произведению производной внешней функции на производную от внутренней функции. Важно, однако, что производная внутренней функции вычисляется в точке x, а производная внешней функции - в точке u = g(x)!

Эта формула легко обобщается на случай, когда сложная функция состоит из нескольких "слоев", вложенных иерархически друг в друга.

Рассмотрим несколько примеров, иллюстрирующих правило производной сложной функции. Это правило широко применяется и во многих других задачах раздела "Дифференцирование".

Пример 1

Найти производную функции .

Решение.

Поскольку , то по правилу производной сложной функции получаем

Пример 2

Найти производную функции .

Решение.

Здесь мы имеем дело с композицией трех функций. Производная тангенса равна . Тогда

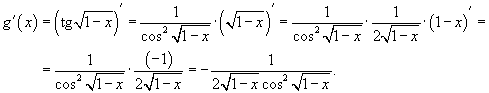
18. Дифференциал функции

Понятие дифференциала функции

Пусть функция у=ƒ(х) имеет в точке х отличную от нуля производную.

Тогда, по теореме о связи функции, ее предела и бесконечно малой функции, можно записать D у/D х=ƒ'(х)+α, где α→0 при ∆х→0, или ∆у=ƒ'(х)•∆х+α•∆х.

Таким образом, приращение функции ∆у представляет собой сумму двух слагаемых ƒ'(х)•∆х и а•∆х, являющихся бесконечно малыми при ∆x→0. При этом первое слагаемое есть бесконечно малая функция одного порядка с ∆х, так как второе слагаемое есть бесконечно малая функция более высокого порядка, чем ∆х:

Поэтому первое слагаемое ƒ'(х)· ∆х называют главной частью приращения функции ∆у.

Дифференциалом функции у=ƒ(х) в точке х называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается dу (или dƒ(х)):

dy=ƒ'(х)•∆х. (24.1)

Дифференциал dу называют также дифференциалом первого порядка. Найдем дифференциал независимой переменной х, т. е. дифференциал функции у=х.

Так как у'=х'=1, то, согласно формуле (24.1), имеем dy=dx=∆x, т. е. дифференциал независимой переменной равен приращению этой переменной: dх=∆х.

Поэтому формулу (24.1) можно записать так:

dy=ƒ'(х)dх, (24.2)

иными словами, дифференциал функции равен произведению производной этой функции на дифференциал независимой переменной.

Из формулы (24.2) следует равенство dy/dx=ƒ'(х). Теперь обозначение

производной dy/dx можно рассматривать как отношение дифференциалов dy и dх.

<< Пример 24.1

Найти дифференциал функции ƒ(х)=3x2-sin(l+2x).

Решение: По формуле dy=ƒ'(х) dx находим

dy=(3х2-sin(l+2x))'dx=(6х-2cos(l+2х))dx.

<< Пример 24.2

Найти дифференциал функции

Вычислить dy при х=0, dx=0,1.

Решение:

Подставив х=0 и dx=0.1, получим

19. Применение дифференциала к приближенным вычислениям

Мы установили, что дифференциал функции является частью ее приращения и отличается от нее на величину . Эта величина при является бесконечно малой функцией более высокого порядка, чем (при ), так как

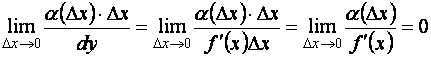
Поэтому при достаточно малых имеет место приближенное равенство или , откуда

При этом чем меньше , тем точнее значение функции.

Равенство (1) представляет собой "рабочую формулу" применения дифференциала к приближенным вычислениям.

Пример. Вычислите приближенно с двумя десятичными знаками .

Решение.

Введем функцию и в качестве возьмем число, наиболее близкое к , но такое, чтобы легко вычислялся и было бы достаточно малым.

В нашем случае удобно взять , тогда . Найдем .

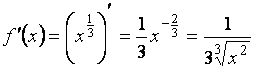Вычислим , .

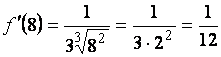Тогда по формуле (1)

.

Ответ:

20.

21. Свойства дифференциала

1. Пусть u = u(x) и v = v(x) – дифференцируемые в точке х функции. Тогда в точке х имеют место следующие формулы:

d(u±v) = du ±dv

d(uv) = udv+vdu

(при условии, что V(x) ¹ 0)

Эти формулы следуют из определения дифференциала и свойств производной.

Пример. y = x3sin2x. Найти dy.

dy = (3x2sin2x+2x3cos2x)dx

22. Теорема Лагранжа

Теорема. Пусть функция дифференцируема в открытом промежутке и сохраняет непрерывность на концах этого промежутка. Тогда существует такая точка , что

Доказательство. Рассмотрим вспомогательную функцию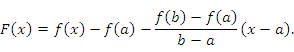

Эта функция непрерывна и дифференцируема в промежутке , а на его концах принимает одинаковые значения:

Тогда удовлетворяет всем условиям теоремы Ролля и, следовательно, существует точка , в которой производная функции равна нулю:

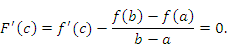
Следствие 1. В частном случае, когда , из теоремы Лагранжа вытекает, что существует точка , в которой производная функции равна нулю: . Это означает, что теорема Лагранжа является обобщением теоремы Ролля.

Следствие 2. Если во всех точках некоторого промежутка , то в этом промежутке.

Действительно, пусть и – произвольные точки промежутка и . Применяя теорему Лагранжа к промежутку , получим

Однако во всех точках промежутка . Тогда

Учитывая произвольность точек и , получаем требуемое утверждение.

Геометрическая интерпретация теоремы Лагранжа. Разностное отношение в правой части формулы (13) есть угловой коэффициент секущей, проходящей через точки и , а производная равна угловому коэффициенту касательной к графику функции в н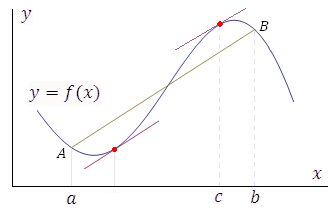 екоторой средней точке промежутка . Поэтому за теоремой Лагранжа закрепилось название “теорема о среднем”.

Рис. 6. Теорема Лагранжа устанавливает условия существования хотя бы одной точки c, в которой касательная к графику функции параллельна секущей AB. Таких точек может быть несколько.

23.

24. Правило Лопиталя — метод нахождения пределов функций, раскрывающий неопределённости вида 0/0 и ∞/∞.

Суть правила: предел отношения функций равен пределу отношения их производных.

Алгоритм вычисления пределов по правилу Лопиталя

Использование правила Лопиталя при нахождении пределов проиллюстрируем следующим примером.

Пример.

Найти .

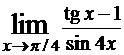
Решение.Сначала убедимся, что правило Лопиталя применить можно. Действительно, величины, стоящие в числителе и знаменателе при x → π/4 являются бесконечно малыми, то есть имеем неопределенность вида 0/0, следовательно можно воспользоваться правилом Лопиталя:

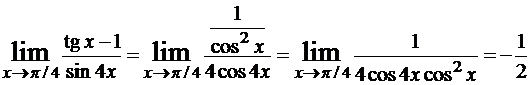
Правило Лопиталя можно применять неоднократно, если отношение производных снова дает неопределенность или .

25. Возрастание и убывание функции на интервале.

Определение возрастающей функции.

Функция y=f(x) возрастает на интервале X, если для любых и выполняется неравенство . Другими словами – большему значению аргумента соответствует большее значение функции.

Определение убывающей функции.

Функция y=f(x) убывает на интервале X, если для любых и выполняется неравенство . Другими словами – большему значению аргумента соответствует меньшее значение функции.

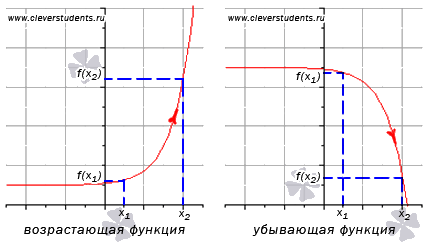
26. Наибольшим значением функции y=f(x) на промежутке X называют такое значение , что для любого справедливо неравенство .

Наименьшим значением функции y=f(x) на промежутке X называют такое значение , что для любого справедливо неравенство .

Эти определения интуитивно понятны: наибольшее (наименьшее) значение функции – это самое большое (маленькое) принимаемое значение на рассматриваемом интервале при абсциссе .

Стационарные точки – это значения аргумента, при которых производная функции обращается в ноль.

Для чего нам стационарные точки при нахождении наибольшего и наименьшего значений? Ответ на этот вопрос дает теорема Ферма. Из этой теоремы следует, что если дифференцируемая функция имеет экстремум (локальный минимум или локальный максимум) в некоторой точке, то эта точка является стационарной. Таким образом, функция часто принимает свое наибольшее (наименьшее) значение на промежутке X в одной из стационарных точек из этого промежутка.

Также часто наибольшее и наименьшее значение функция может принимать в точках, в которых не существует первая производная этой функции, а сама функция определена.

Сразу ответим на один из самых распространенных вопросов по этой теме:"Всегда ли можно определить наибольшее (наименьшее) значение функции"? Нет, не всегда. Иногда границы промежутка X совпадают с границами области определения функции или интервал X бесконечен. А некоторые функции на бесконечности и на границах области определения могут принимать как бесконечно большие так и бесконечно малые значения. В этих случаях ничего нельзя сказать о наибольшем и наименьшем значении функции.

Для наглядности дадим графическую иллюстрацию. Посмотрите на рисунки – и многое прояснится.

На отрезке

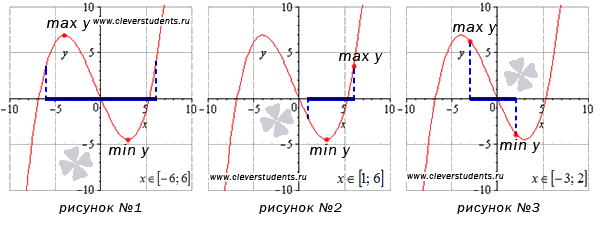
На первом рисунке функция принимает наибольшее (max y) и наименьшее (min y) значения в стационарных точках, находящихся внутри отрезка [-6;6].

Рассмотрим случай, изображенный на втором рисунке. Изменим отрезок на [1;6]. В этом примере наименьшее значение функции достигается в стационарной точке, а наибольшее - в точке с абсциссой, соответствующей правой границе интервала.

На рисунке №3 граничные точки отрезка [-3;2] являются абсциссами точек, соответствующих наибольшему и наименьшему значению функции.