10. Числовой последовательностью называется бесконечное множество чисел

следующих одно за другим в определенном порядке и построенных по определенному закону, с помощью которого задается как функция целочисленного аргумента, т.е. .

Число а называется пределом последовательности и обозначается ,

Число а называется пределом последовательности , если для любого существует номер такой, что для любого выполняется неравенство :

Числовая последовательность не может иметь более одного предела. Последовательность, имеющая предел, называется сходящейся.

Для сходящихся последовательностей имеют место теоремы:

.

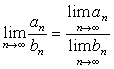
11. Предел функции по Коши

Значение называется пределом (предельным значением) функции в точке , если для

любой окрестности точки существует выколотая окрестность точки такая, что образ этой окрестности лежит в . Фундаментальное обоснование данного определения предела можно найти в статье Предел вдоль фильтра.

12. Свойства предела функции.

• Если функция f заданная на множестве Х имеет конечный предел в точке х0, тогда найдется окрестность U этой точки, такая, что функция f будет ограничена на пересечении U и Х.

• Если функция f заданная на множестве Х имеет конечный и не равный 0 предел а в точке х0, тогда найдется окрестность U этой точки и положительное число c, такие,

что при a > 0 на пересечении верно f(x) > c ;

а при a < 0 на пересечении U и Х верно f(x) < – c.

• Если f(x) = C для всех x, тогда предел этой функции равен C. Если f(x) і C для всех x, тогда предел этой функции больше или равен C.

• Если g(x) Ј f(x) Ј h(x) и пределы функций g и <h в точке х0 равны между собой и равны a, то предел f(x) в этой точке также равен a.

• Если у функцийg(x) и f(x) существуют пределы, равные a и b соответственно, тогда выполняются следующие арифметические свойства пределов :

Именуемые пределом линейной комбинации (суммы), пределом произведения пределом отношения.

• Для вычисления предела суперпозиции функций g(f(x)) нужно вычислить предел , а затем нужно вычислить предел g(x) при условии, что x à a.

13. Непрерывная функция — функция без «скачков», то есть такая, у которой малые изменения аргумента приводят к малым изменениям значения функции.

Функция f (x), определенная в некоторой окрестности точки a, называется непрерывной в этой точке, если

Свойства непрерывных функций

Теорема. Если f(x) и g(x) непрерывны в точке x0, то в этой же точке непрерывны и функции f(x) ± g(x), f(x) × g(x) и f(x)/g(x) (последнее только в случае, если g(x0)¹0).

Определение. Пусть y = f(x) и x = j(t). Тогда комбинация y = f(j(t)) называется суперпозицией функций f(x) и j(t), или сложной функцией.

Теорема о непрерывности сложной функции.

Пусть x = j(t) непрерывна в точке t0, а функция f(x) непрерывна в точке x0 = j(t0). Тогда функция y = f(j(t)) непрерывна в точке t0.

Короче говоря, суперпозиция непрерывных функций есть также непрерывная функция.

1 4. Наряду с непрерывностью функции в точке рассматривают ее непрерывность на разных промежутках.

Функция f(x) называется непрерывной на интервале (a, b), если она непрерывна в каждой точке этого интервала.

Функция f(x) называется непрерывной на отрезке [a, b], если она непрерывна на интервале (a, b), непрерывна справа в точке a и непрерывна слева в точке b.

Замечание. Функция, непрерывная на отрезке [a,b] может быть разрывной в точках a и b (рис. 1)

Множество функций, непрерывных на отрезке [a, b] обозначается символом C[a, b].

Свойства функций, непрерывных на отрезке

Теорема 1 (об ограниченности непрерывной функции). Если функция f(x) непрерывна на отрезке [a, b], то она ограничена на этом отрезке, т.е. существует такое число C> 0, что "x О [a, b] выполняется неравенство |f(x)| ≤ C.

Т еорема 2 (Вейерштрасс). Если функция f(x) непрерывна на отрезке [a, b], то она достигает на этом отрезке своего наибольшего значения M и наименьшего значения m, т.е. существуют точки α, β О [a, b] такие, что m = f(α) ≤ f(x) ≤ f(β) = M для всех x О [a, b] (рис.2).

Наибольшее значение M обозначается символом maxx О [a, b] f(x), а наименьшее значение m — символом minx О [a, b] f(x).

Теорема 3 (о существовании нуля). Если функция f(x) непрерывна на отрезке [a, b] и на концах отрезка принимает ненулевые значения разных знаков, то на интервале (a, b) найдется по крайней мере одна точка ξ в которой f(ξ) = 0.

Геометрический смысл теоремы состоит в том, что график функции, удовлетворяющей условиям теоремы, обязательно пересечет ось OX (рис.3).

З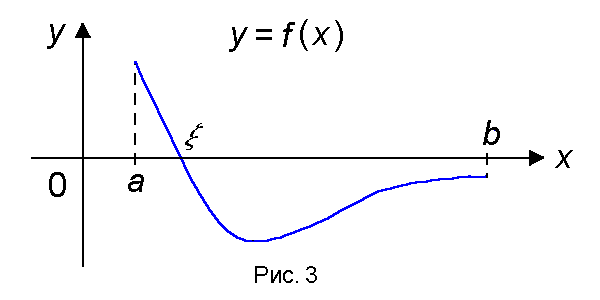 амечание. На этой теореме основан метод приближенного решения уравнения

f(x) = 0, (1)

называемый методом бисекции (дихотомии), или методом половинного деления.

15. Производной функции f(x) (f'(x0)) в точке x0 называется число, к которому стремится разностное отношение , стремящемся к нулю.

Производные элементарных функций.

Правила дифференцирования.

Если у функций f(x) и g(x) существуют производные, то

Производная сложной функции:

Геометрический смысл производной. Производная в точке x0 равна угловому коэффициенту касательной к графику функции y=f(x) в этой точке

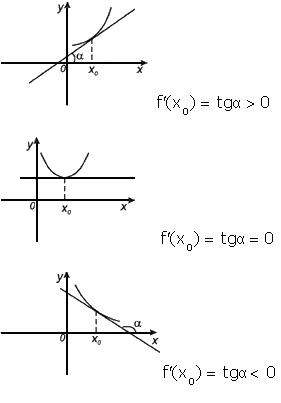
Уравнение касательной к графику функции y=f(x) в точке x0 :

Физический смысл производной.

Если точка движется вдоль оси х и ее координата изменяется по закону x(t), то мгновенная скорость точки:

16. Производная и ее свойства

Определение: Пусть функция определена в точке и в некоторой ее окрестности. Дадим аргументу приращение , такое, чтобы не выйти из указанной окрестности. Найдем соответствующее приращение функции и составим отношение. Если существует предел этого отношения при стремящемся к нулю, то указанный предел называют производной функции в точке и обозначают . Иначе говоря:

(— приращение функции, — приращение аргумента).

Если в каждой точке из множества у функции существует производная, то такая функция называется дифференцируемой на множестве .

Правила дифференцирования

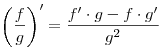
Основные формулы дифференцирования.