4. Определители матриц и их свойства

Квадратную матрицу порядка n можно сопоставить с числом (или , или ), называемым определителем или детерминантом.

Вычисление определителя:

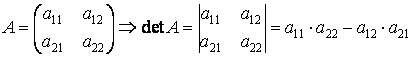
т. е. правило:

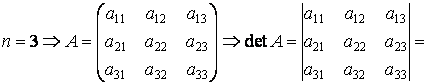
т. е. Правило треугольника (или Саррюса):

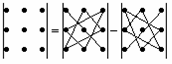
Отметим следующие свойства определителей:

– определители не изменяются, если его строки заменить столбцами и наоборот (строки и столбцы это ряд определителя);

– при перестановке двух параллельных рядов определитель меняет знак;

– определитель, имеющий два одинаковых ряда, равен нулю;

– общий множитель элементов какого-либо рода определителя можно вынести за знак определителя;

– если элементы какого-либо ряда определителя представляют собой суммы двух слагаемых, то определитель может быть разложен на сумму соответственных определителей;

– определитель не изменяется, если к элементам одного ряда прибавить соответствующие элементы параллельного ряда, умноженные на любое число;

Дальнейшие свойства связаны с понятием минора и алгебраического дополнения.

.

5. http://www.webmath.ru/primeri_reshenii/primeri_reshenii_slay_kramer1_11.php

Условие

5x 1 - x 2 - x 3 = 0

x 1 + 2x 2 + 3x 3 = 14

4x 1 + 3x 2 + 2x 3 = 16

Решение системы линейных алгебраических уравнений методом Крамера

Для проверки ответов можете воспользоваться нашим онлайн сервисом - Решение системы линейных уравнений методом Крамера. Если после изучения примеров решения задач у Вас останутся вопросы, то Вы всегда можете задать их на форуме, и не забывайте про наши онлайн калькуляторы для решения задач по геометрии и другим предметам!

Систему уравнений можно представить в матричной форме: Ax = B, где А - основная матрица (квадратная матрица), В - матрица свободных членов.

Теперь необходимо найти 4 определителя: определитель основной матрицы (определитель системы) и 3 определителя дополнительных матриц. Перед нахождением определителей советуем ознакомиться с теорией определителей матриц, а для нахождения определителей советуем использовать нашу программу - нахождение определителя матрицы.

Перепишем систему линейных алгебраических уравнений в матричную форму. Слева от разделительной линии стоят коэффициенты при переменных, а справа стоят свободные члены.

5

-1

-1

1

2

3

4

3

2

0

14

16

Найдем определитель основной матрицы:

Δ =

5

-1

-1

1

2

3

4

3

2

= 5 · 2 · 2 - 1 · 3 · 4 - 1 · 1 · 3 + 1 · 2 · 4 - 3 · 3 · 5 + 2 · 1 · 1 = -30

Определитель основной матрицы не равен нуля, значит система невырожденная.

Найдем определители 3 дополнительных матриц:

Дополнительная матрица получается из основной путем замены элементов одного из трех столбцов основной матрицы элементами матрицы свободных членов.

Δ 1 =

0

-1

-1

14

2

3

16

3

2

= 0 · 2 · 2 - 1 · 3 · 16 - 1 · 14 · 3 + 1 · 2 · 16 - 3 · 3 · 0 + 2 · 1 · 14 = -30

Δ 2 =

5

0

-1

1

14

3

4

16

2

= 5 · 14 · 2 + 0 · 3 · 4 - 1 · 1 · 16 + 1 · 14 · 4 - 3 · 16 · 5 - 2 · 0 · 1 = -60

Δ 3 =

5

-1

0

1

2

14

4

3

16

= 5 · 2 · 16 - 1 · 14 · 4 + 0 · 1 · 3 - 0 · 2 · 4 - 14 · 3 · 5 + 16 · 1 · 1 = -90

Найдем решения системы алгебраических уравнений:

х1 = Δ1/Δ = 1

х2 = Δ2/Δ = 2

х3 = Δ3/Δ = 3

Условие

3x 1 + 3x 2 + 6x 3 + 3x 4 = 6

3x 1 + x 2 + 5x 3 + x 4 = 2

2x 1 + x 2 + 4x 3 + 2x 4 = 1

x 1 + 3x 2 + 3x 3 + 2x 4 = 6

http://www.webmath.ru/primeri_reshenii/primeri_reshenii_slay_gauss2_2.php

Решение системы линейных алгебраических уравнений методом Гаусс

Для проверки ответов можете воспользоваться нашим онлайн сервисом - Решение системы линейных уравнений методом Гаусса. Все действия описанные в данном разделе не противоречат правилам обращения с матрицами и являются элементарными преобразованиями матрицы. Если после изучения примеров решения задач у Вас останутся вопросы, то Вы всегда можете задать их на форуме, и не забывайте про наши онлайн калькуляторы для решения задач по геометрии и другим предметам!

Перепишем систему линейных алгебраических уравнений в матричную форму. Получится матрица 4 × 5, слева от разделительной линии стоят коэффициенты при переменных, а справа стоят свободные члены.

3

3

6

3

3

1

5

1

2

1

4

2

1

3

3

2

6

2

1

6

Проведём следующие действия:

Строку № 1 поделим на 3 (Строка 1 = строка 1 / 3)

Получим:

1

1

2

1

3

1

5

1

2

1

4

2

1

3

3

2

2

2

1

6

Проведём следующие действия:

Из строки № 2 вычтем строку № 1 умноженную на 3 (Строка 2 - 3 × строка 1)

Из строки № 3 вычтем строку № 1 умноженную на 2 (Строка 3 - 2 × строка 1)

Из строки № 4 вычтем строку № 1 (Строка 4 - строка 1)

Получим:

1

1

2

1

0

-2

-1

-2

0

-1

0

0

0

2

1

1

2

-4

-3

4

Проведём следующие действия:

Строку № 3 поделим на -1 (Строка 3 = строка 3 / -1)

Поменяем местами строку № 2 и строку № 3

Получим:

1

1

2

1

0

1

0

0

0

-2

-1

-2

0

2

1

1

2

3

-4

4

Проведём следующие действия:

К строке № 3 прибавим строку № 2 умноженную на 2 (Строка 3 + 2 × строка 2)

Из строки № 4 вычтем строку № 2 умноженную на 2 (Строка 4 - 2 × строка 2)

Получим:

1

1

2

1

0

1

0

0

0

0

-1

-2

0

0

1

1

2

3

2

-2

Проведём следующие действия:

К строке № 4 прибавим строку № 3 (Строка 4 + строка 3)

Строку № 4 умножим на -1 (Строка 4 = строка 4 * -1)

Получим:

1

1

2

1

0

1

0

0

0

0

-1

-2

0

0

0

1

2

3

2

0

Проведём следующие действия:

К строке № 3 прибавим строку № 4 умноженную на 2 (Строка 3 + 2 × строка 4)

Из строки № 1 вычтем строку № 4 (Строка 1 - строка 4)

Получим:

1

1

2

0

0

1

0

0

0

0

-1

0

0

0

0

1

2

3

2

0

Проведём следующие действия:

К строке № 1 прибавим строку № 3 умноженную на 2 (Строка 1 + 2 × строка 3)

Из строки № 1 вычтем строку № 2 (Строка 1 - строка 2)

Строку № 3 умножим на -1 (Строка 3 = строка 3 * -1)

Получим:

1

0

0

0

0

1

0

0

0

0

1

0

0

0

0

1

3

3

-2

0

В левой части матрицы по главной диагонали остались одни единицы. В правом столбце получаем решение:

х1 = 3

х2 = 3

х3 = -2

х4 = 0

6. Числа вида z =x+iy назовём комплексными числами. Ко́мпле́ксные чи́сла— расширение поля вещественных чисел, обычно обозначается . Первоначально обнаружены в результате формального решения некоторых квадратных уравнений, в которых квадрат корня уравнения должен быть отрицательным.

7. Действия над комплексными числами

Сравнение

Означает , (два комплексных числа равны между собой тогда и только тогда, когда равны их действительные и мнимые части).

Сложение

Вычитание

Умножение

Деление

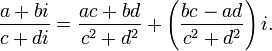
8. Функцией называется закон, по которому числу х из заданного множества Х, поставлено в соответствие только одно число у, пишут , при этом x называют аргументом функции, y называют значением функции.

Существуют разные способы задания функций.

1. Аналитический способ.

Аналитический способ - это наиболее часто встречающийся способ задания функции.

Заключается он в том, что функция задается формулой, устанавливающей, какие операции нужно произвести над х, чтобы найти у. Например .

Рассмотрим первый пример - . Здесь значению x = 1 соответствует , значению x = 3 соответствует и т. д.

Функция может быть задана на разных частях множества X разными функциями.

Например:

Во всех ранее приведенных примерах аналитического способа задания, функция была задана явно. То есть, справа стояла переменная y, а справа формула от переменной х. Однако, при аналитическом способе задания, функция может быть задана и неявно.

Например . Здесь, если мы задаем переменной x значение, то, чтобы найти значение переменной у (значение функции), мы должны решить уравнение. Например, для первой заданной функции при х = 3, будем решать уравнение:

. То есть, значение функции при х = 3 равно -4/3.

При аналитическом способе задания, функция может быть задана параметрически - это, когда х и у выражены через некоторый параметр t. Например,

Здесь при t = 2, x = 2, y = 4. То есть, значение функции при х = 2 равно 4.

2. Графический способ.

При графическом способе вводится прямоугольная система координат и в этой системе координат изображается множество точек с координатами (x,y). При этом . Пример:

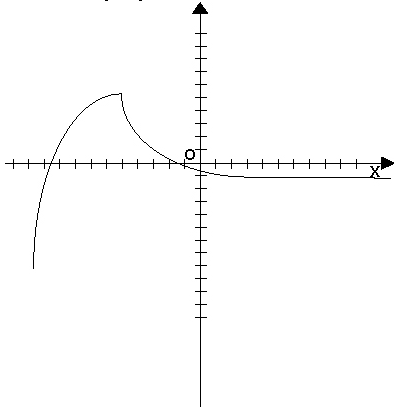
3. Словесный способ.

Функция задается с помощью словесной формулировки. Классический пример – функция Дирихле.

«Функция равна 1, если х – рациональное число; функция равна 0, если х – иррациональное число».

4. Табличный способ.

Табличный способ наиболее удобен, когда множество Х конечно. При этом способе составляется таблица, в которой каждому элементу из множества Х, ставится в соответствие число Y.

Пример:

Табличный способ задания функции очень удобен при обработке результатов исследований. Например, при выявлении зависимости между уровнем загрязнения окружающей среды и количеству людей, заболевших раком.

9. Числовая последовательность — это последовательность элементов числового пространства.

Пусть — это либо множество вещественных чисел , либо множество комплексных чисел . Тогда последовательность элементов множества называется числовой последовательностью.

Бесконечно большие и бесконечно малые последовательности .

Бесконечно малая последовательность — это последовательность, предел которой равен нулю.

Бесконечно большая последовательность — это последовательность, предел которой равен бесконечности.

Свойства бесконечно малых последовательностей

Бесконечно малые последовательности отличаются целым рядом замечательных свойств, которые активно используются в математическом анализе, а также в смежных с ним и более общих дисциплинах.

Сумма двух бесконечно малых последовательностей сама также является бесконечно малой последовательностью.

Разность двух бесконечно малых последовательностей сама также является бесконечно малой последовательностью.

Алгебраическая сумма любого конечного числа бесконечно малых последовательностей сама также является бесконечно малой последовательностью.

Произведение ограниченной последовательности на бесконечно малую последовательность есть бесконечно малая последовательность.

Произведение любого конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность.

Любая бесконечно малая последовательность ограничена.

Если стационарная последовательность является бесконечно малой, то все её элементы, начиная с некоторого, равны нулю.

Если вся бесконечно малая последовательность состоит из одинаковых элементов, то эти элементы — нули.

Если — бесконечно большая последовательность, не содержащая нулевых членов, то существует последовательность , которая является бесконечно малой. Если же всё же содержит нулевые элементы, то последовательность всё равно может быть определена, начиная с некоторого номера , и всё равно будет бесконечно малой.

Если — бесконечно малая последовательность, не содержащая нулевых членов, то существует последовательность , которая является бесконечно большой. Если же всё же содержит нулевые элементы, то последовательность всё равно может быть определена, начиная с некоторого номера , и всё равно будет бесконечно большой.