8,21. Розв’язування систем алгебраїчних рівнянь методом оберненої матриці.

Матрицею називається прямокутна таблиця із чисел, яка містить m рядків та п стовпців, взята в квадратні або круглі дужки Оберненою для заданої квадратної матриці А називається така матриця , добуток на яку матриці А рівний одиничній матриці, тобто Або коротко В цьому випадку вважають, що матриця має розмірність т × n. Матриці позначають латинськими буквами А, В, С, Е,. Обернена матриця існує тільки для невироджених матриць, тобто коли Матриця, яка складена із алгебраїчних доповнень елементів транспонованої матриці, називається приєднаною (або союзною ) до матриці А. Позначимо через А матрицю, складену із коефіцієнтів при невідомих(так звану основну матрицю системи); X - матрицю-стовпець із невідомих; В - матрицю-стовпець із вільних членів, тобто

Тоді систему рівнянь можна переписати у вигляді матричного рівняння: АХ=В. Визначник матриці А називається визначником системи. Помноживши зліва в цьому рівнянні на А^-1, одержимо Враховуючи, що , одержимо матричний розв'язок системи Знаходження матричного розв'язку називається матричним способом розв'язування системи лінійних рівнянь.

Приклад. Записати і розв'язати в матричній формі систему рівнянь Позначимо через

Система лінійних рівнянь запишеться у матричній формі АХ=В. Матричний розв'язок системи буде Для знаходження оберненої матриці обчислимо визначник

Так як то для матриці А існує обернена , а значить можна знайти єдиний розв'язок вихідної системи. Запишемо транспоновану матрицю Знайдемо алгебраїчні доповнення до елементів транспонованої матриці:

Запишемо приєднану матрицю Обернена матриця має вигляд Знайдемо розв'язок заданої системи: Розв'язок системи лінійних рівнянь такий:

9,10, 22 Обчислення визначених інтегралів методом лівих (правих)(середніх) прямокутників.

Найпростіший метод наближеного обчислення інтеграла на ЕОМ є метод прямокутників, суть якого зводиться до знаходження визначеного інтегралу як суми площ N прямокутників (з висотою f(x) та основою ), отриманих шляхом розбиття відрізка інтегрування [а, b] на N рівних частин. В цьому випадку розділити на прямокутники можна або зліва на право (рис.7.2,а), тоді отримаємо формулу лівих прямокутників (7.1), або справа наліво (рис.7.2,б), тоді отримаємо формулу правих прямокутників (7.2):

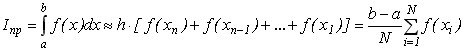     (7.1)

    

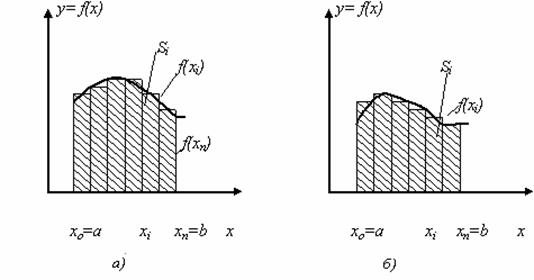
     Рисунок 7.2 – Геометрична інтерпретація методу прямокутників

     (7.2)

11. Обчислення визначених інтегралів методом трапецій.

Суть методу трапецій полягає в тому, що інтеграл обчислюється таким чином: відрізок інтегрування [а, b] поділяється на N рівних відрізків, всередині яких підінтегральна крива f(x) замінюється кусково-лінійною функцією (х), отриманою стягуванням ординат N відрізків [x_i-1, x_i ] хордами.Інтеграл знаходиться як сума площ S_i прямокутних трапецій (pис.7.4 а,б).

    

     Рисунок 7.4– Геометрична інтерпретація метода трапецій

Площа кожної такої трапеції визначається як     . Відповідно на всьому відрізку інтегрування [а, b] площа складної фігури, яка визначається як сума площин всіх таких трапецій, визначається формулою:

     . Оскільки в даної формулі під знаком суми величини зустрічаються двічі, тому її можна переписати у вигляді:

     Похибка обчислення інтеграла за формулою трапеції визначається:   . Схема алгоритму обчислення інтегралу методом трапецій показано на рис.