3.Розв’язування рівнянь з однією змінною методом хорд.

Нехай на відрізку міститься один корінь рівняння.Припустимо, що функція та її похідні , неперервні на відрізку і похідні , не змінюють знаку на цьому відрізку. Припустимоадляпвизначеності,що при ( випадок зводитьсяпдоппопереднього, якщо рівняння записати у вигляді - . Тоді графік функції буде вгнутим на . Можливі два в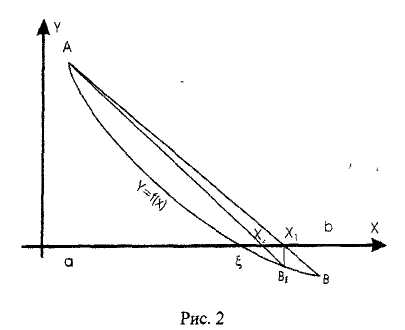 ипадки: 1) ; 2) . Розглянемо ці випадки.1) .Складемо рівняння хорди АВ і знайдемо абсцису , точки перетину цієї хорди з віссю Ох. Тут позначено . Складемо рівняння хорди і знайдемо абсцису точки перетину цієї хорди з віссюОх. Можнаанаписатипформулу для довільного n: , У цьому випадку кінець а нерухомий. Послідовність є обмеженою монотонно спадною послідовністю. Отже, вона має границю Перейшовши до границі при у рівності (1.9), отримаємо: .Звідси випливає, що , тобто є коренем рівняння. .У другому випадку нерухомим є кінець . Знайдемо, як і в першому випадку, абсциси точок перетину хорд з віссю . Отримаємо формули: У рівності позначено .Отже, , Послідовність є обмеженою монотонно зростаючою послідовністю. Тому вона має границю , причому є коренем рівняння (доведення проводиться так само, як і у першому випадку). За наближене значення кореня можна взяти , обчислене за формулою (1.9) або (1.12). Для оцінки точності цього наближення користуються формулою: де - найменше значення на відрізку , тобто при .

5.Розв’язування рівнянь з однією змінною методом простої ітерації.

Одним із найважливіших способів наближеного розв'язання рівняння є метод ітерацій, який часто називають методом послідовних наближень. Нехай функція ї та її похідні і , неперервні на відрізку , де міститься тільки один корінь рівняння . Запишемо це рівняння у вигляді Виберемо на відрізку деяким способом наближене значення кореня , рівняння (1.25) і побудуємо числову послідовність за формулою .Справедлива наступна теорема. Нехай функція визначена та диференційовна на відрізку , причому усі її значення належать цьому відрізку. Тоді, якщо існує таке додатне число , що при , то: послідовність збігається незалежно від початкового значення є границя цієї послідовності є коренем рівняння (1.25) на відрізку .Похибка наближеного значення кореня , знайденого методом ітерацій, оцінюється нерівністю: _. Для того, щоб знайти наближене значення кореня з абсолютною похибкою, яка не перевищує заданого числа , достатньо визначити n так, щоб виконувалася нерівність . Дане рівняння можна записати у вигляді різними способами. З наведеної теореми випливає, що повинна виконуватись умова у деякому околі шуканого кореня . Чим менше число q, тим швидше, послідовні наближення збігаються до кореня Наведемо один досить загальний спосіб зведення рівняння до вигляду (1.25). Замінимо рівняння еквівалентним йому рівнянням де число . Позначимо .Підберемо параметр так, щоб похідна була малою по абсолютній величині на відрізку . Наприклад, можна припустити, що , або , або Зауважимо, що при виконанні умов наведеної теореми метод ітерації збігається при будь-якому виборі початкового значення є . Завдяки цьому окрема помилка в обчисленнях, яка не виводить за межі відрізка , не впливає на остаточний результат, оскільки помилкове значення можна розглядати як нове початкове наближення . Можливо тільки, що збільшиться обсяг обчислювальної роботи. Властивість самовиправлення робить метод ітерації одним із найпоширеніших методів обчислень.